Пример решения задачи
Для электрической цепи, схема которой изображена на рисунке, выполнить расчет по условиям задания. Дополнительно построить потенциальную диаграмму для внешнего контура цепи. Параметры элементов схемы имеют следующие значения:
| E1=30 B; | E2=16 B; | E3=10 B; | R1=2 Ом; | R2=5 Ом; |
| R3=3 Ом; | R4=1 Ом; | R5=8 Ом; | R6=5Ом. |
При расчете схемы будем придерживаться порядка, указанного в задании. Выберем направления токов в ветвях и составим уравнения по первому закону Кирхгофа для независимых узлов 1, 2, 3.
| Составим уравнения по первому закону Кирхгофа для независимых узлов 1, 2, 3. | 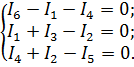
|
| Выберем три независимых контура 1, 2, 3. И укажем направление их обхода. Составим для этих контуров уравнения по второму закону Кирхгофа: | 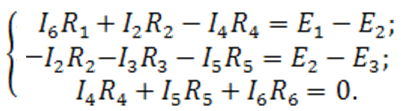
|
| Выполним расчет цепи по методу контурных токов. При расчете цепи по методу контурных токов вначале нужно составить уравнения и определить значения контурных сопротивлений и напряжений источников. Если в схеме содержатся источники тока, то их предварительно заменяют эквивалентными источниками напряжения. | 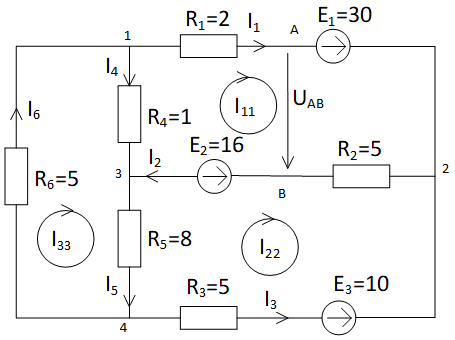
|
| Уравнения контурных токов для этой схемы имеют вид: где | 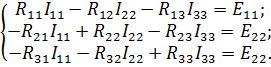
|
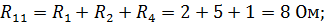
| 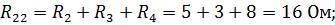
|
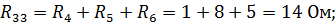
| |
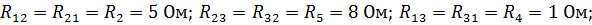
| |
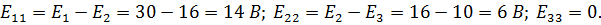
| |
| После подстановки значений контурных сопротивлений и напря-жений источников получим систе-му контурных уравнений: | 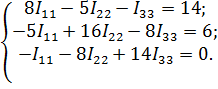
|
| Вычислим контурные токи, пользуясь этими уравнениями: | 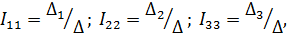
|
| Значения определителей для контурных токов будут равны: | |
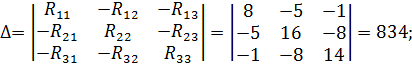
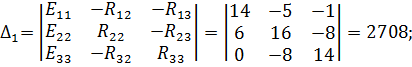
|
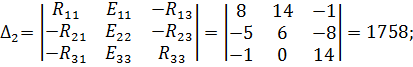
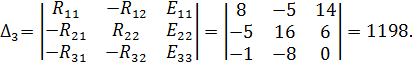
| ||
Подставив значения определителей, вычислим значения контурных токов:
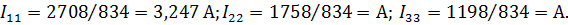 Используя значения контурных токов, найдем токи в ветвях цепи:
Используя значения контурных токов, найдем токи в ветвях цепи:
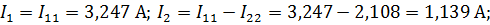
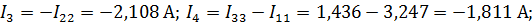
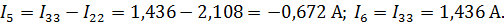
| ||
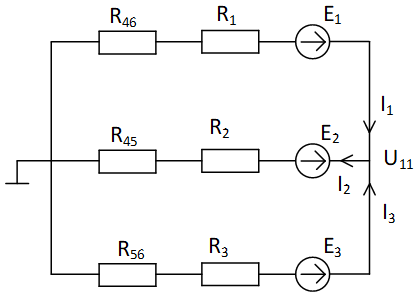
Упростим схему, заменив соединение сопротивлений 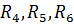 на эквивалентное соединение сопро-тивлений звездой. Полученная схема после преобразования, приведена справа, и её сопротивления преобра-зованных ветвей принимают значения: на эквивалентное соединение сопро-тивлений звездой. Полученная схема после преобразования, приведена справа, и её сопротивления преобра-зованных ветвей принимают значения:
| 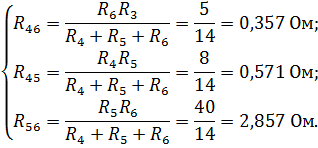
| |
Выполним расчет преобразован-ной схемы методом узловых напряжений. В полученной схеме имеются только два узла, поэтому для нее можно составить только одно уравнение по методу узловых напряжений: 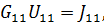
| 
| |
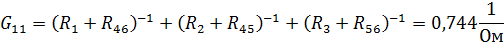
| ||
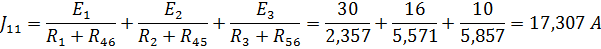
| ||
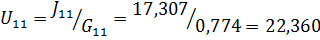
| 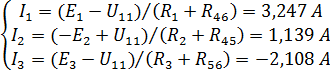
| |
Т. о., токи, рассчитанные методами узловых напряжений и контурных токов совпадают, что подтверждает корректность решения задачи.
Определим ток в сопротивлении R6, пользуясь методом эквивалентного генератора. Считаем, что сопротивление R6 является нагрузкой, исключим его, разорвав ветвь, в которую оно было включено. Или, как говорят, разрешим цепь относительно R6, считая оставшуюся часть активным двухполюсником (см. исходную схему).
| Затем для полученной части схемы найдем напряжение холостого хода и ее входное сопротивление (пассивного двухполюсника). В результате схема сводится к цепи, которая изображена справа. | 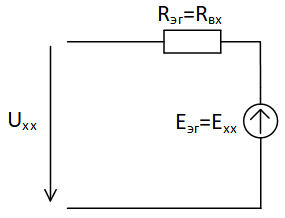
|
Найдем токи в исходной цепи при исключенной ветви с R6. Для этого воспользуемся методом контурных токов.
| Уравнения цепи, составленные по методу контурных токов, имеют вид: | 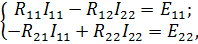
| |
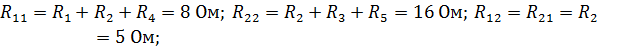
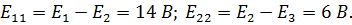
| ||
| Подставим значения сопротивлений и напряжений, получим систему уравнений: | 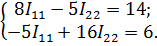
| |
| В результате решения этой системы уравнений находи токи: | 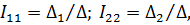
| |
| Значения определителей для контурных токов будут равны | ||
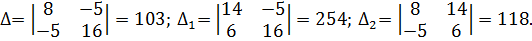
| ||
| Подставив значения определителей, найдем токи в ветвях цепи: | ||
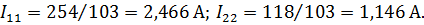
| ||
| Напряжение холостого хода на зажимах подключения нагрузки: | 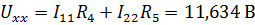
| |
Для определения входного сопротивления необходимо исключить из схемы источники напряжения, заменив их перемычками. При расчете входного сопротивления произведем замену треугольника сопротивлений эквивалентной звездой.
| Значение сопротивлений эквивалентной звезды найдем по формулам: | 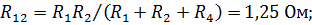 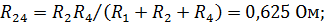
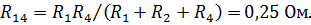
| |
Расчет входного сопротивления:
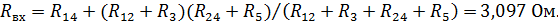
| ||
| Ток в сопротивлении R6 равен: | 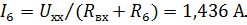
| |
Этот результат точно совпадает со значением тока, полученным ранее по методу контурных токов, что подтверждает правильность выполненного расчета.
Составим баланс мощности для исходной схемы. При составлении баланса мощностей учтем, что мощность, потребляемая всеми элементами цепи, должна быть равна мощности, которую отдают источники энергии. Однако возможна такая ситуация, при которой ток в каком - либо источнике имеет направление, противоположное напряжению этого источника. В этом случае источник не отдает энергию во внешнюю цепь, а, наоборот, потребляет ее. Как указывалось, выше, такое положение может иметь место, например, при зарядке аккумулятора.
При составлении баланса мощностей найдем вначале мощности источников напряжения:
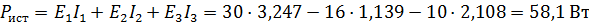
Из этого уравнения следует, что мощность в цепь отдает только источник Е1, а два других источника Е2 и Е3 ее потребляют.
Теперь найдем мощность, которую потребляют сопротивления цепи:
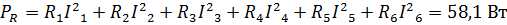
Таким образом, можно считать, что баланс мощностей выполняется, так как 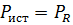
Дата добавления: 2021-12-14; просмотров: 545;











