Метод узловых напряжений
Метод узловых напряжений основан на введении промежуточных неизвестных переменных – узловых напряжений.
Узловое напряжение – напряжение между i-м узлом схемы и одним определенным, произвольно выбранным опорным узлом.
Уравнения составляются на основе первого закона Кирхгофа т.е. (у-1) . Определив узловые напряжения, находят напряжения между узлами цепи и токи ветвей по закону Ома для участка цепи.
Примечание:
Так как любой узел схемы может быть заземлен без изменения токораспределения в ней, то, принимая потенциал опорного узла равным нулю, вместо узловых напряжений в качестве переменных можно ввести потенциалы узлов Ui0=φi- φ0= φi. В этом случае метод называют методом узловых потенциалов.
Алгоритм решения
1. Выбрать произвольно опорный узел.
2. Для каждого из узлов составить узловые уравнения на основании первого закона Кирхгофа.
| 1 узел | 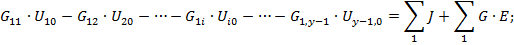
|
| 2 узел | 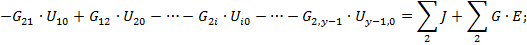
|
| y-1 узел | 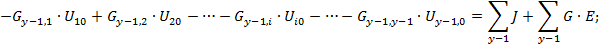
|
где
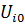 – узловое напряжение i – го узла относительно опорного;
– узловое напряжение i – го узла относительно опорного;
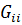 – сумма проводимостей ветвей, сходящемся в узле i.
– сумма проводимостей ветвей, сходящемся в узле i.
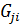 – сумма проводимостей ветвей, соединяющих узлы i и j.
– сумма проводимостей ветвей, соединяющих узлы i и j.
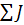 – алгебраическая сумма токов ветвей, соединенных с узлом i, взятых со знаком плюс, если ток источника направлен к узлу i.
– алгебраическая сумма токов ветвей, соединенных с узлом i, взятых со знаком плюс, если ток источника направлен к узлу i.
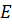 – алгебраическая сумма произведений ЭДС ветвей, соединенных с узлом i, на их проводимости, взятых со знаком плюс, если ЭДС направлена к узлу.
– алгебраическая сумма произведений ЭДС ветвей, соединенных с узлом i, на их проводимости, взятых со знаком плюс, если ЭДС направлена к узлу.
3. Объединив полученные узловые уравнения в систему линейных алгебраических уравнений и подставив числовые значения параметров, решить систему и найти напряжения. Произвольно выбрав направления токов в ветвях, найденных по закону Ома для участка цепи.
4. Проверить правильность полученного решения с помощью уравнения баланса мощности цепи.
Метод двух узлов для схемы, содержащей два узла, можно составить только одно узловое уравнение, из которого можно найти напряжение между этими узлами.
| Задача 1.24 | Схема 1.24 | |||
| Дано: E1=36B; E2=12B; J=8A; R1=R2=4 Ом; R3=1 Ом; R4=3 Ом; R5=1 Ом. Определить токи в ветвях. | 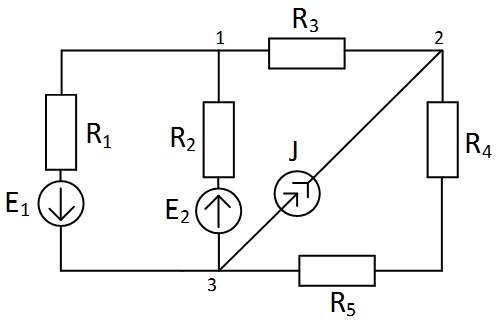
| |||
| Решение. | ||||
| Пусть опорным узлом будет узел 0 цепи. | 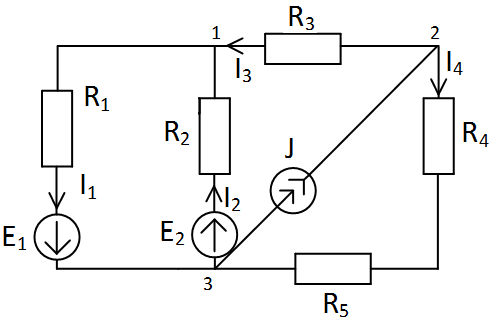
| |||
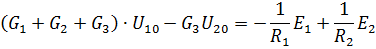
| ||||
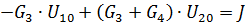
| ||||
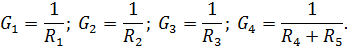
| ||||
| Контурные уравнения цепи: | 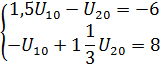
| 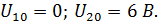
| ||
| Контурные токи | ||||
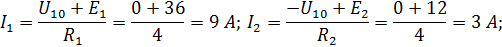
| ||||
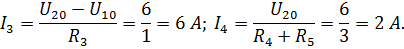
| ||||
| Баланс мощности: | ||||
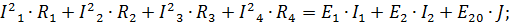
| ||||

| Баланс мощности подтверждается. Решение верно. | |||
| Задача 1.25 | Схема 1.25 | |
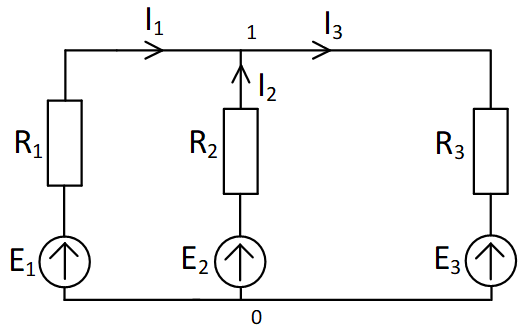
| Дано: E1=10 B; E2=20 B; E3=3 B; R1=4 Ом; R2= 7 Ом; R3=1 Ом. Определить токи в ветвях. | 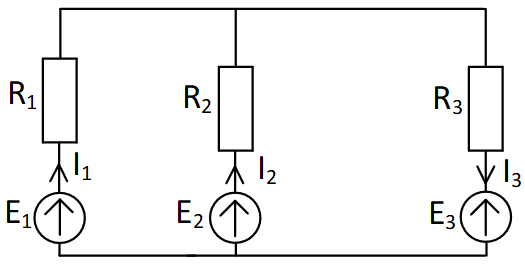
| |
| Решение. | ||
| Так как в расчетной схеме два узла, то согласно методу, двух узлов | ||
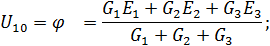
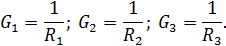
| 
| |
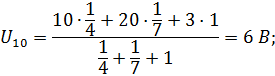
| 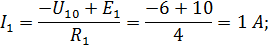
| |
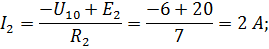
| 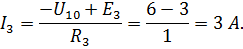
| |
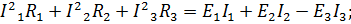
| ||
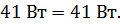
| Баланс мощности подтверждается. Решение верно. | |
| Задача 1.26 | Схема 1.26 | ||||
| Дано: E1=36B; E2=12B; J=8A; R1=R2=4 Ом; R3=1 Ом; R4=3 Ом. Определить токи в ветвях. | 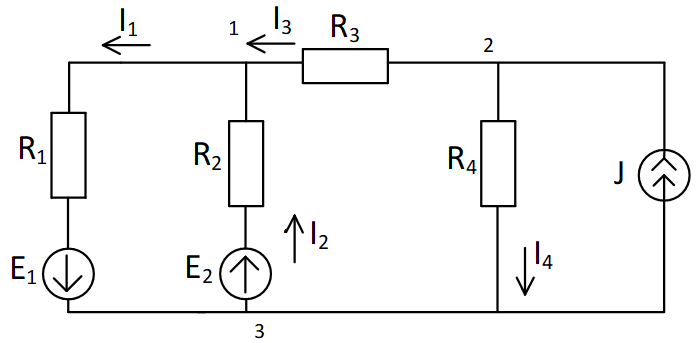
| ||||
| Решение. | |||||
| Примем за опорный узел 3. Составим уравнение по М.У.Н. | 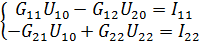
| ||||
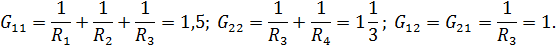
| |||||
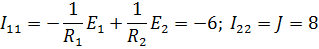
| Откуда 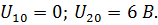
| ||||
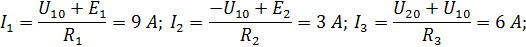
| |||||
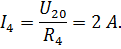
| Уравнение баланса мощности: | ||||
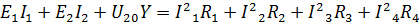
| |||||
Ответ: 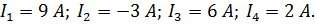
| 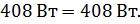
| ||||
| Баланс мощности подтверждается. Решение верно. | |||||
Метод наложения
Метод наложения основан на принципе наложения: ток в любой ветви равен алгебраической сумме токов, вызываемых в этой ветви каждым источником в отдельности.
Находят токи в заданной ветви поочередно от каждого источника, а затем их алгебраически суммируют. Схему рассчитывают столько раз, сколько источников действует в схеме. Каждый раз в схеме оставляют только один источник, от которого определяют токи в ветвях.
Остальные источники удаляют из схемы. При этом источники ЭДС, закорачивают, а ветви с источниками токов, размыкают. Алгоритм решения.
1. Определить величины и направления частичных токов во всех ветвях расчетной схемы, вызванных действием каждого из источников.
2. Выбрать произвольно положительные направления токов ветвей. Найти их путем алгебраического сложения частичных токов этих ветвей.
3. Проверить правильность полученного решения с помощью уравнения баланса мощности цепи.
| Задача 1.27 | Схема 1.27 | |
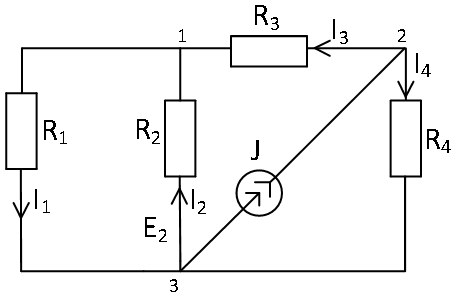
| Дано: E1=36B; E2=12B; J=8A; R1=R2=4 Ом; R3=1 Ом; R4=3 Ом. Определить токи в ветвях. | 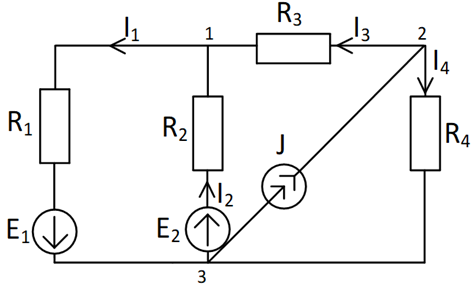
| |
| Решение. | ||
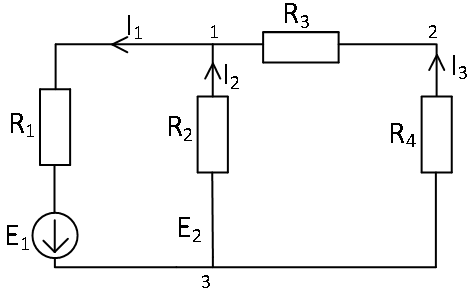
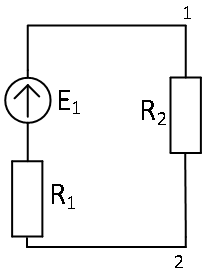
С помощью закона Ома рассчитываем частичные токи в ветвях цепи от действия источника E1.
Расчетная схема 1.
Токи от действия ЭДС E1:
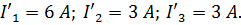
| 
| |
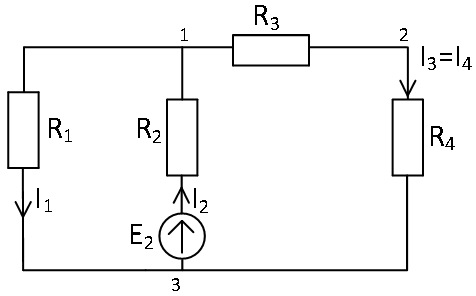
Расчетная схема 2.
Токи от источника ЭДС E2:
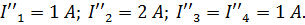
| 
| |
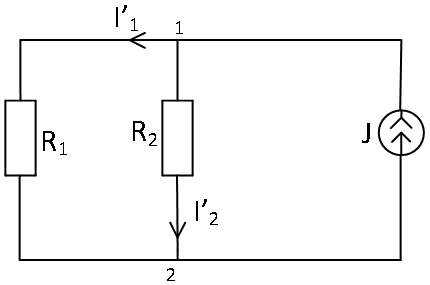
Расчетная схема 3.
Токи от действия источника J:
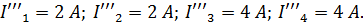
| 
| |
| Выбираем произвольно положительные направления токов ветвей. | ||
| Находим токи ветвей по найденным частичным с учетом направлений искомых и частичных токов. | 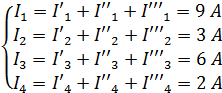
| |
| Для проверки решения составим уравнение баланса мощности. | ||
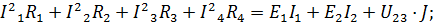
| ||
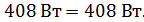
| Баланс мощности подтверждается. Решение верно. | |
| Задача 1.28 | Схема 1.28 |
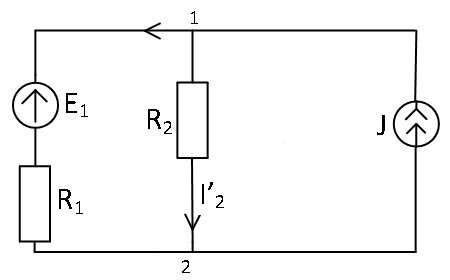
| Дано: E1=100 B; J=1 A; R1=20 Ом; R2=40Ом. Определить токи в ветвях. | 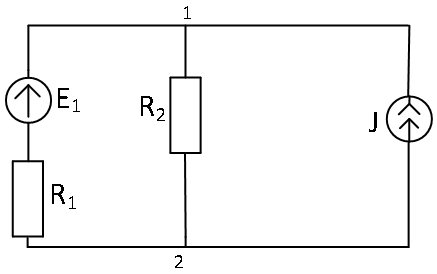
|
| Решение. | |
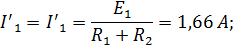
| 
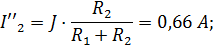
|
| 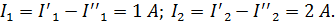
|
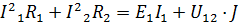
| |
| Баланс мощности | 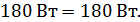
|
Дата добавления: 2021-12-14; просмотров: 1095;











