Вопрос 47. Критические параметры движения по опрокидыванию.
Условие потери устойчивости, при котором происходит опрокидывание – достижение равенства нулю нормальных реакций на внутренних колесах обеих мостов. Запишем условие равновесия при движении на вираже:
( Р  cos
cos 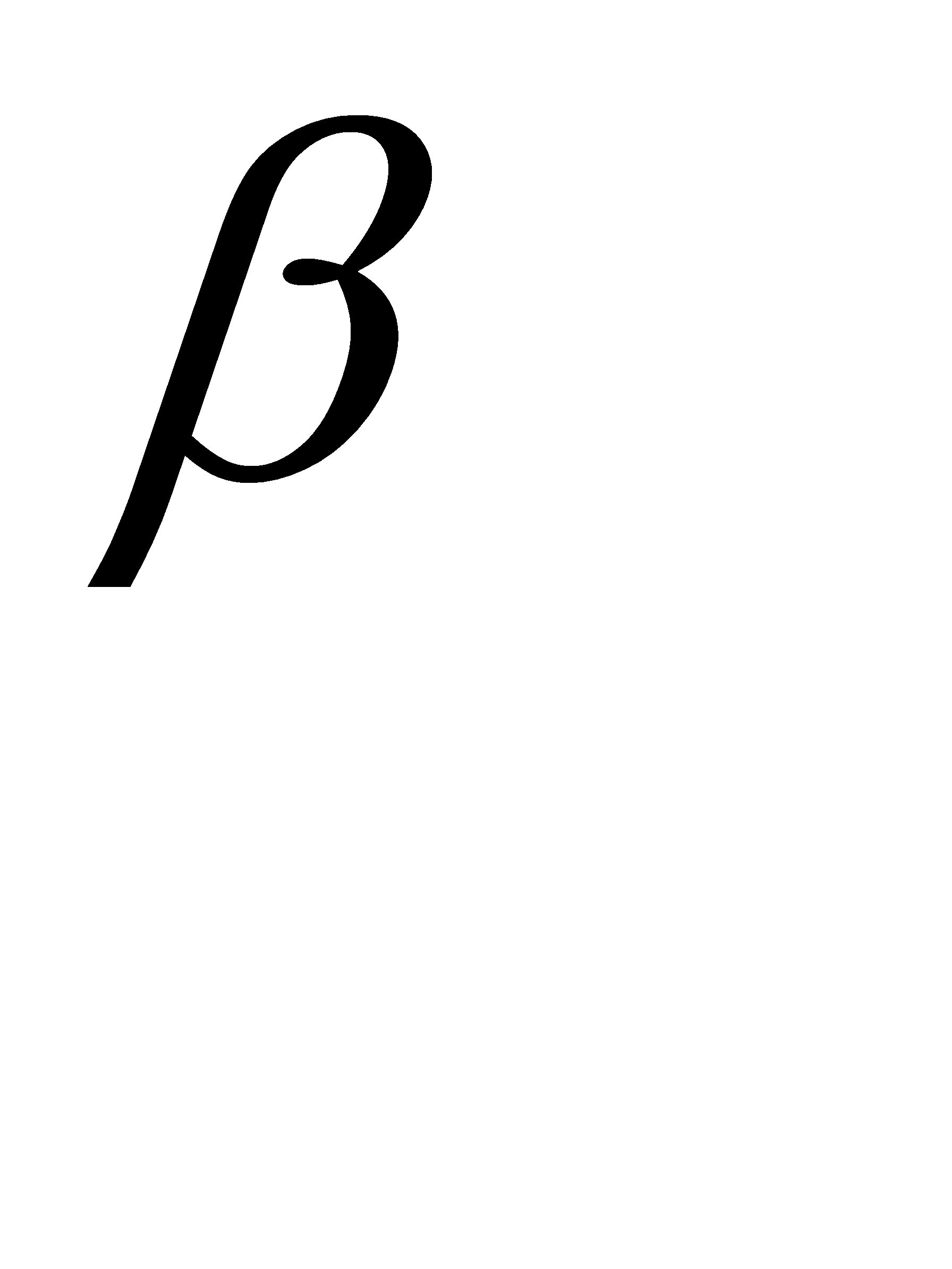 - G
- G 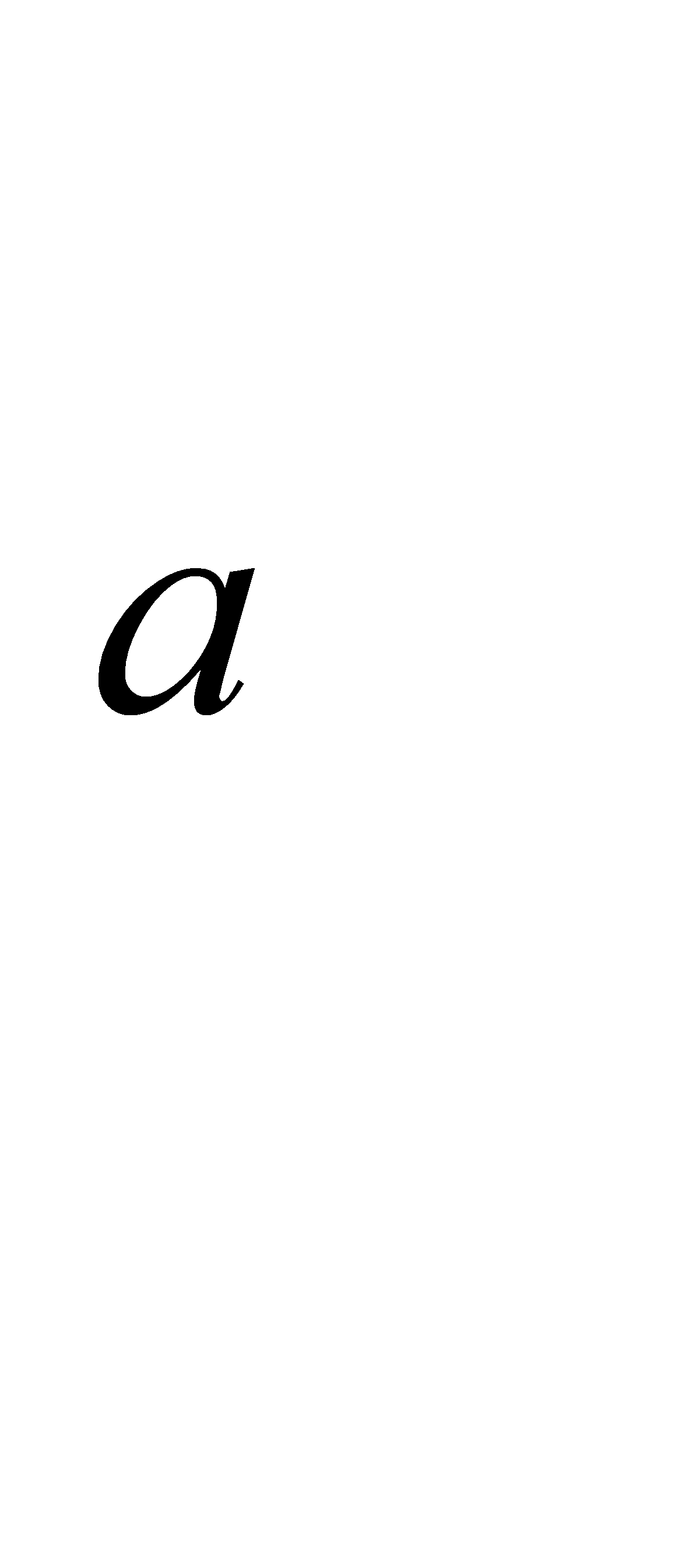 sin
sin 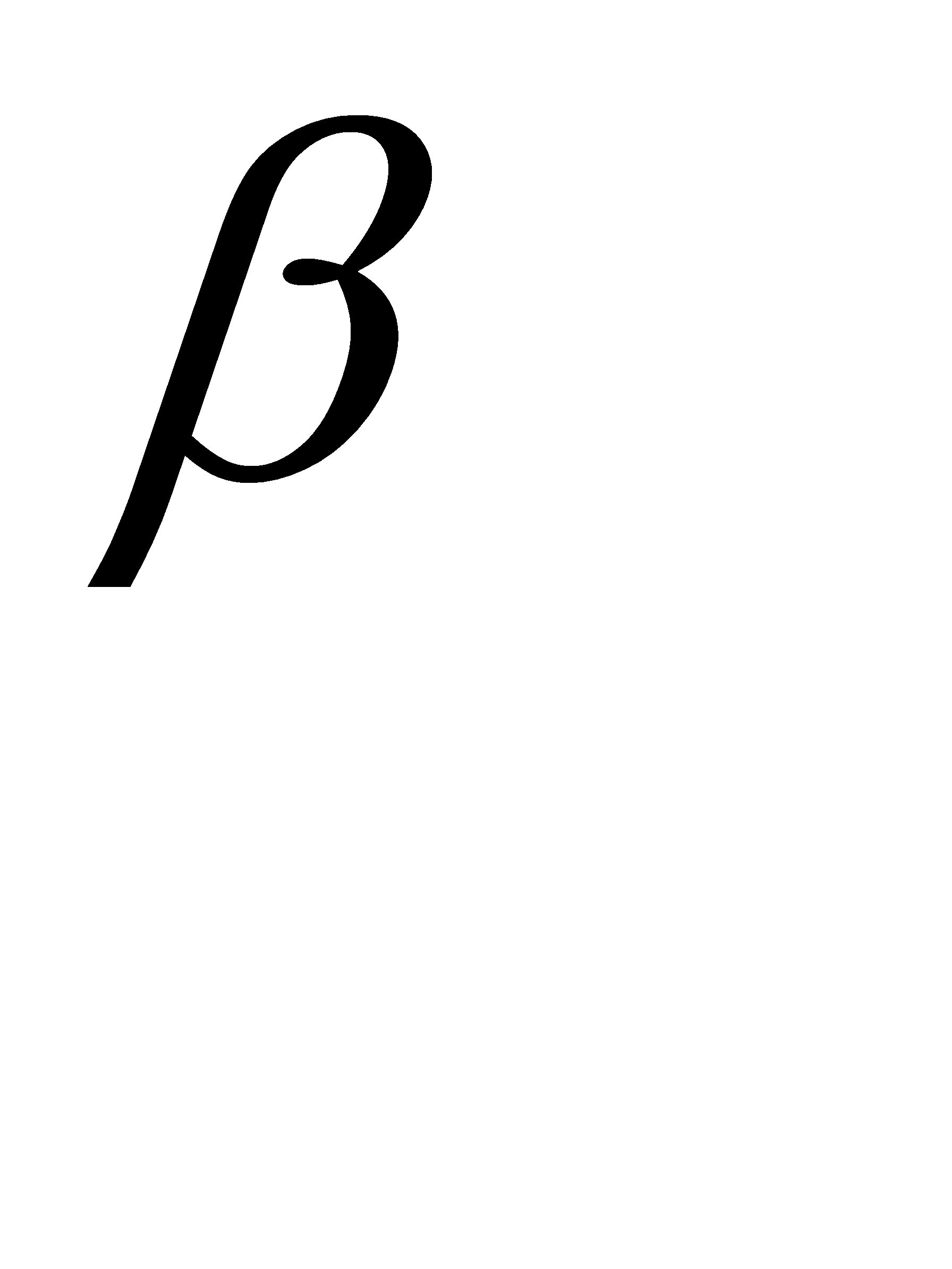 )h
)h 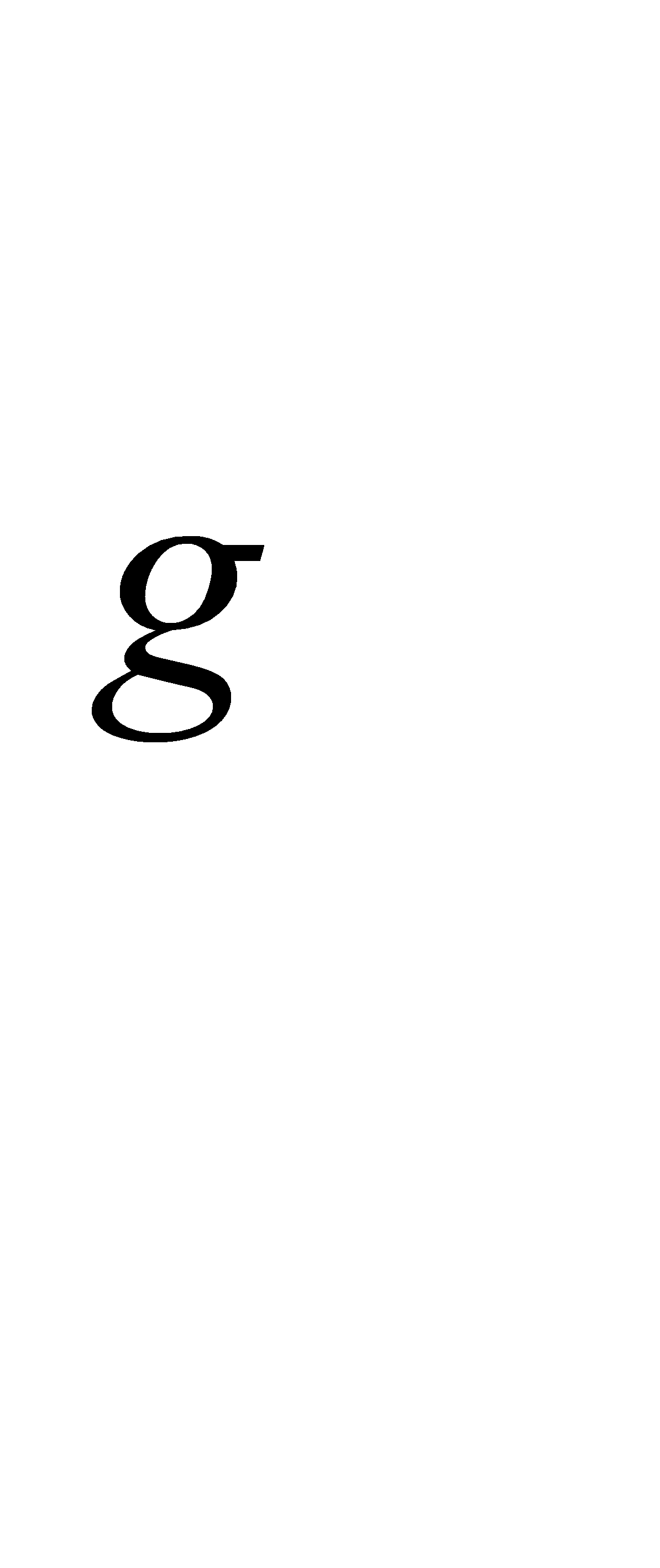 = (G
= (G 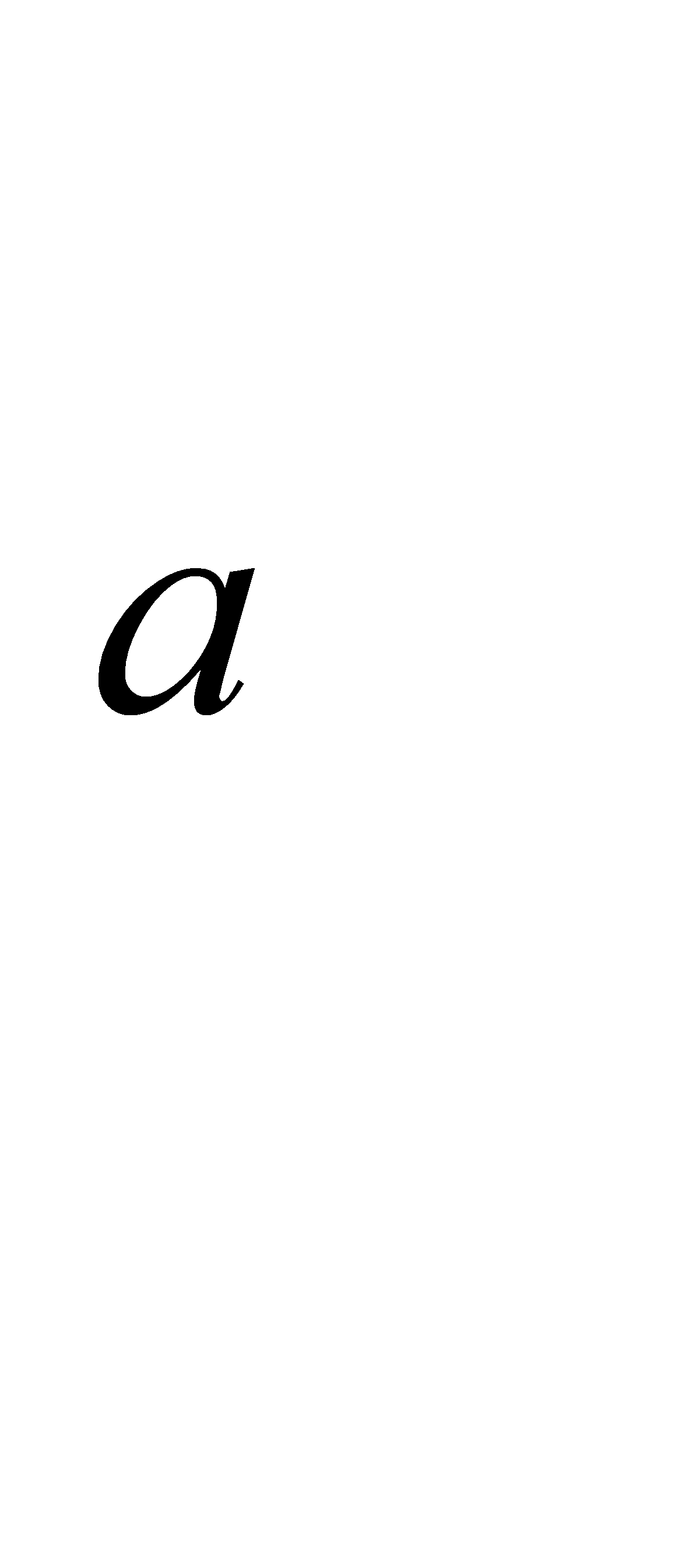 cos
cos 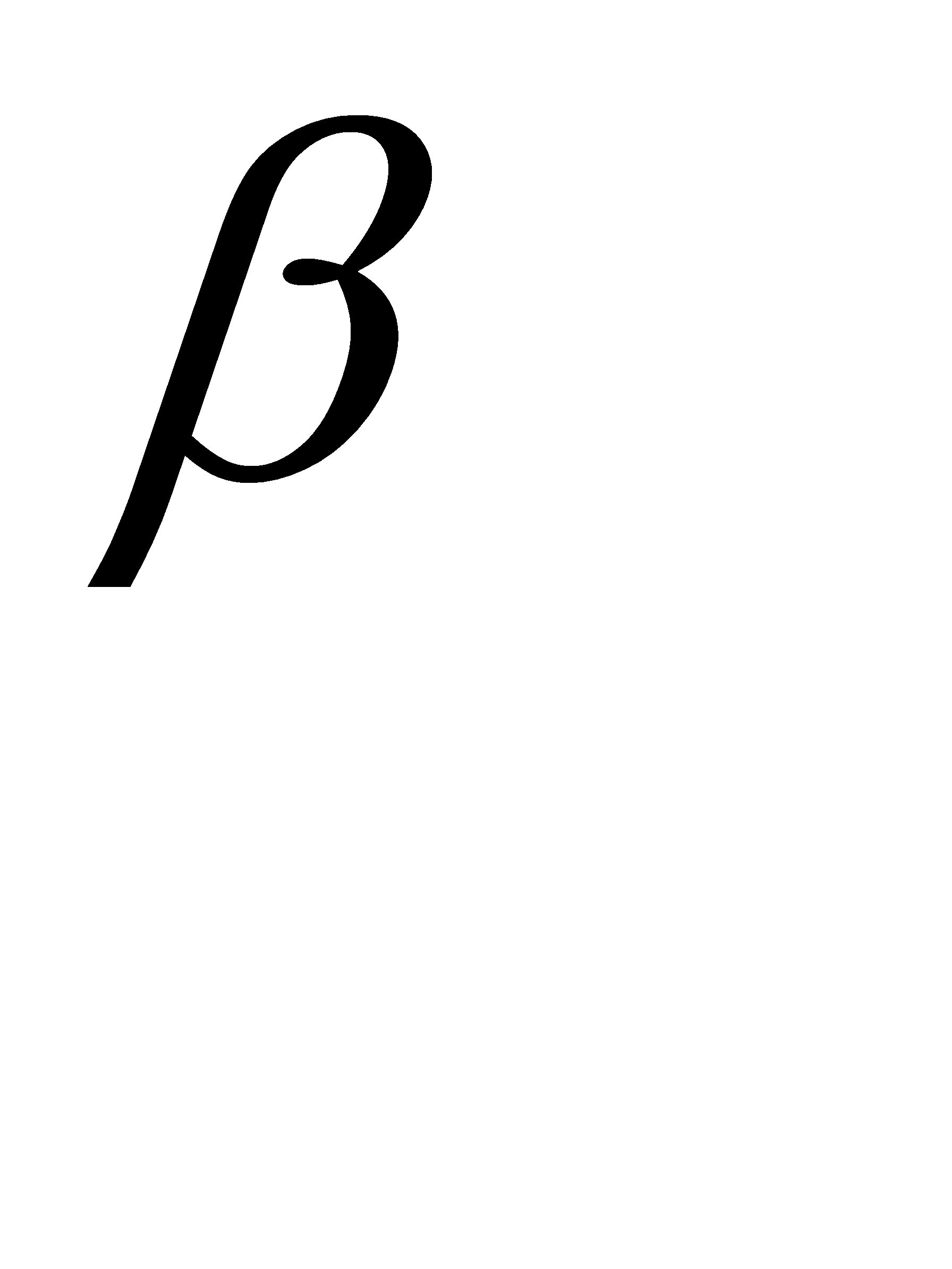 + Р
+ Р  sin
sin 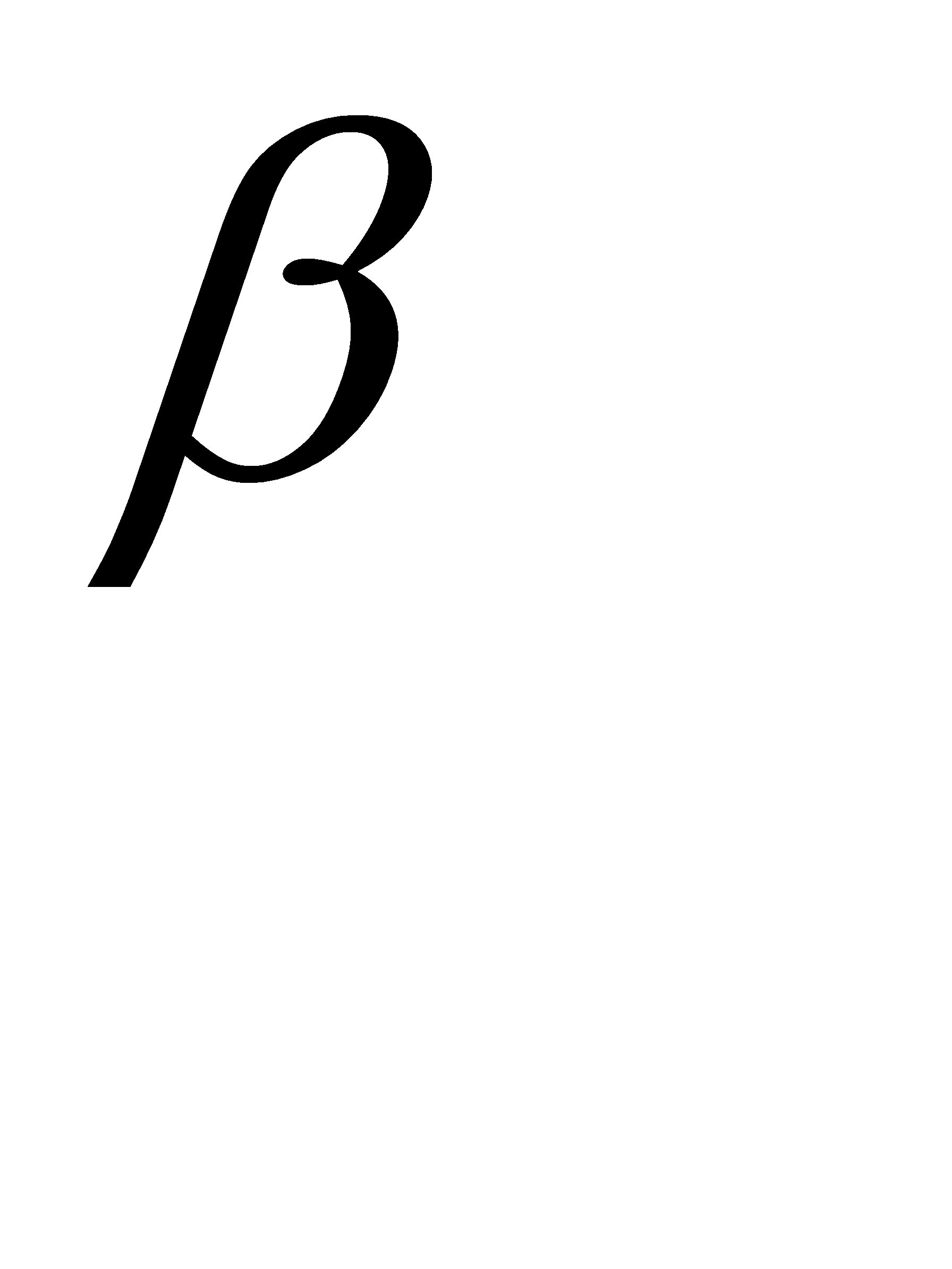 )m, (4.7)
)m, (4.7)
Размер плеча m зависит от целого ряда факторов:
- расположения центра масс в поперечной и продольной плоскостях
- колеи передних и задних колес
- угловой жесткости подвески и плеча крена, определяющих смещение центра подрессоренной массы. Принимая как допущение, что плечо m равно половине колеи, рассмотрим случай опрокидывания в сторону действия силы Р  . Подставляя в полученное выражение Р
. Подставляя в полученное выражение Р  = m
= m 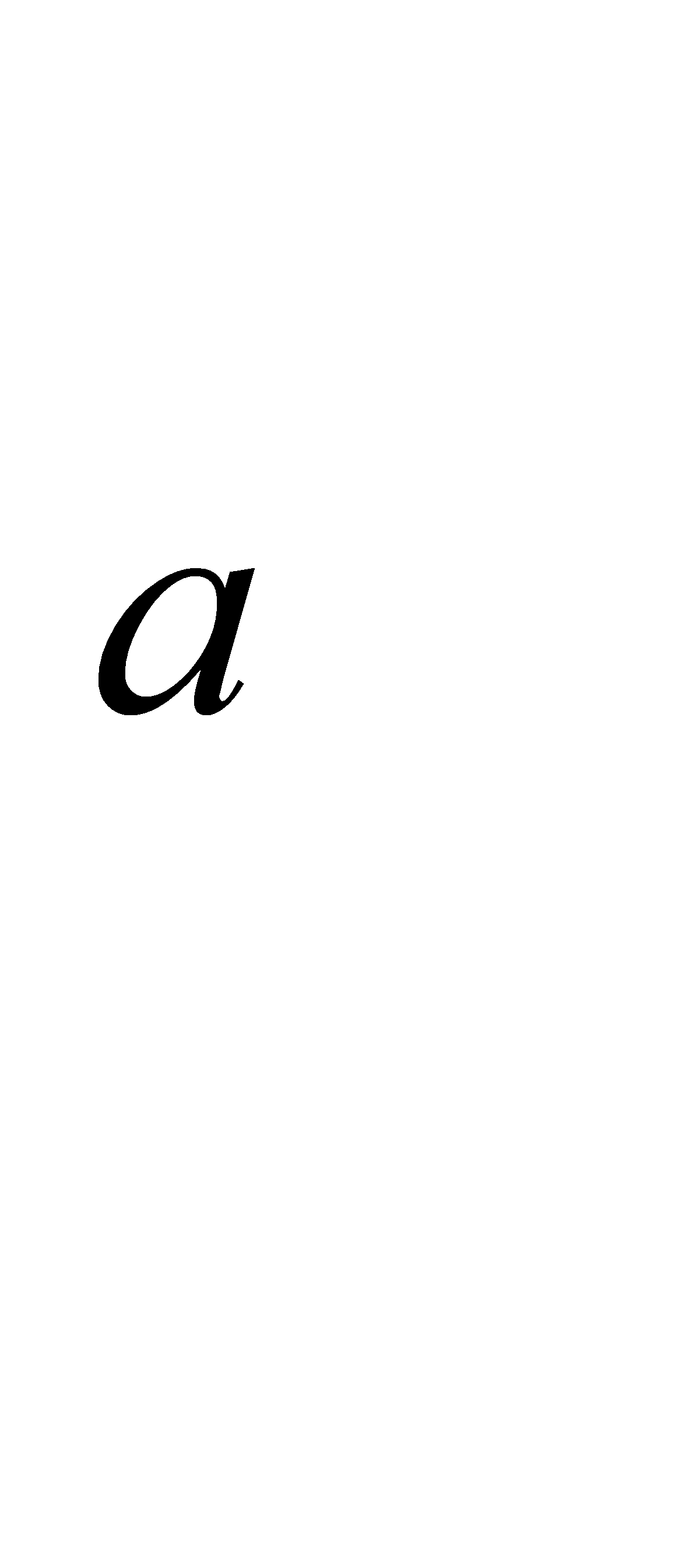 V
V 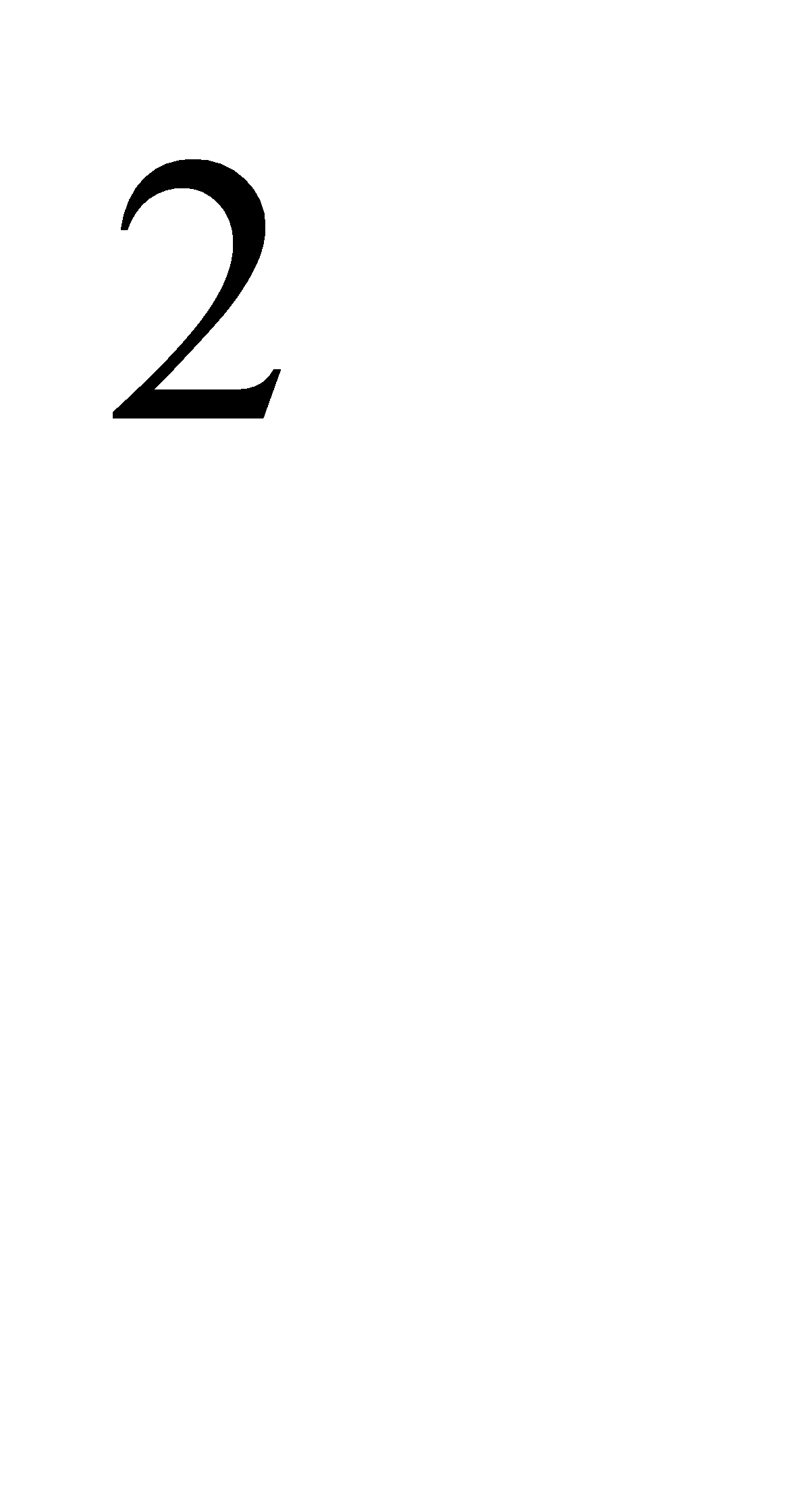 /R и m = В/2 и решая относительно скорости, имеем:
/R и m = В/2 и решая относительно скорости, имеем:
V  =
= 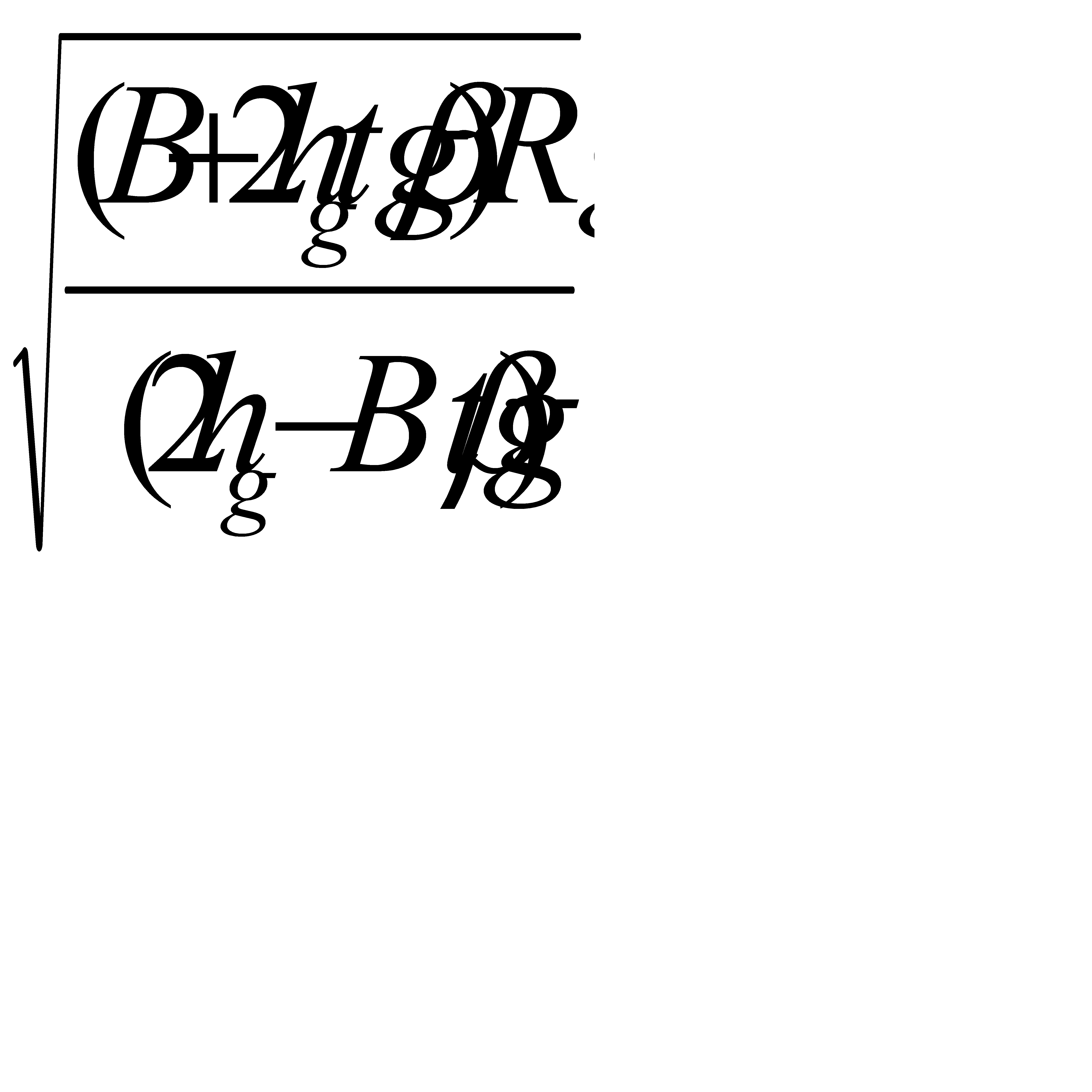 , (4.8)
, (4.8)
Соответственно, при движении по горизонтальной дороге:
V  =
= 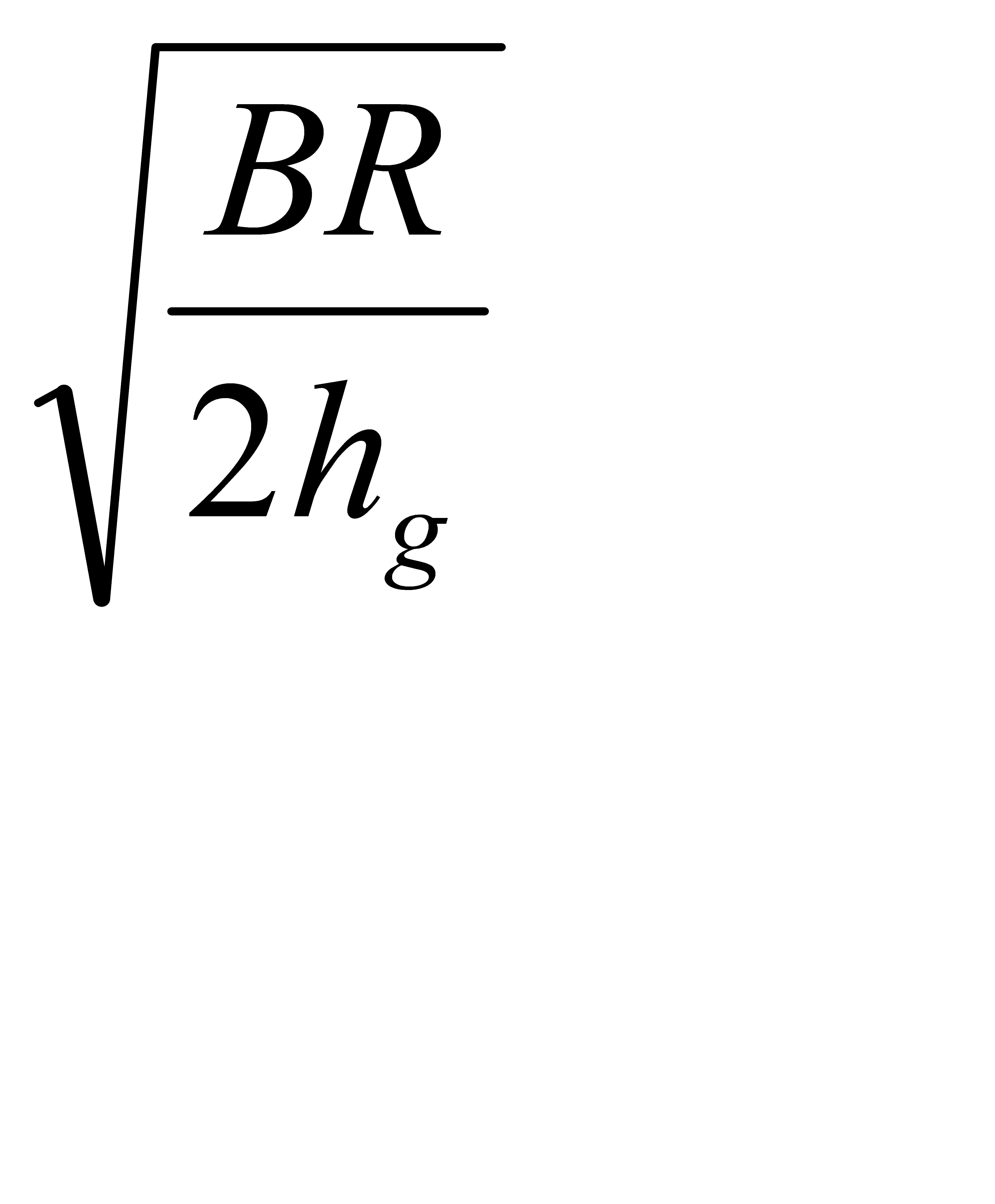 , (4.9)
, (4.9)
Если Р  cos
cos 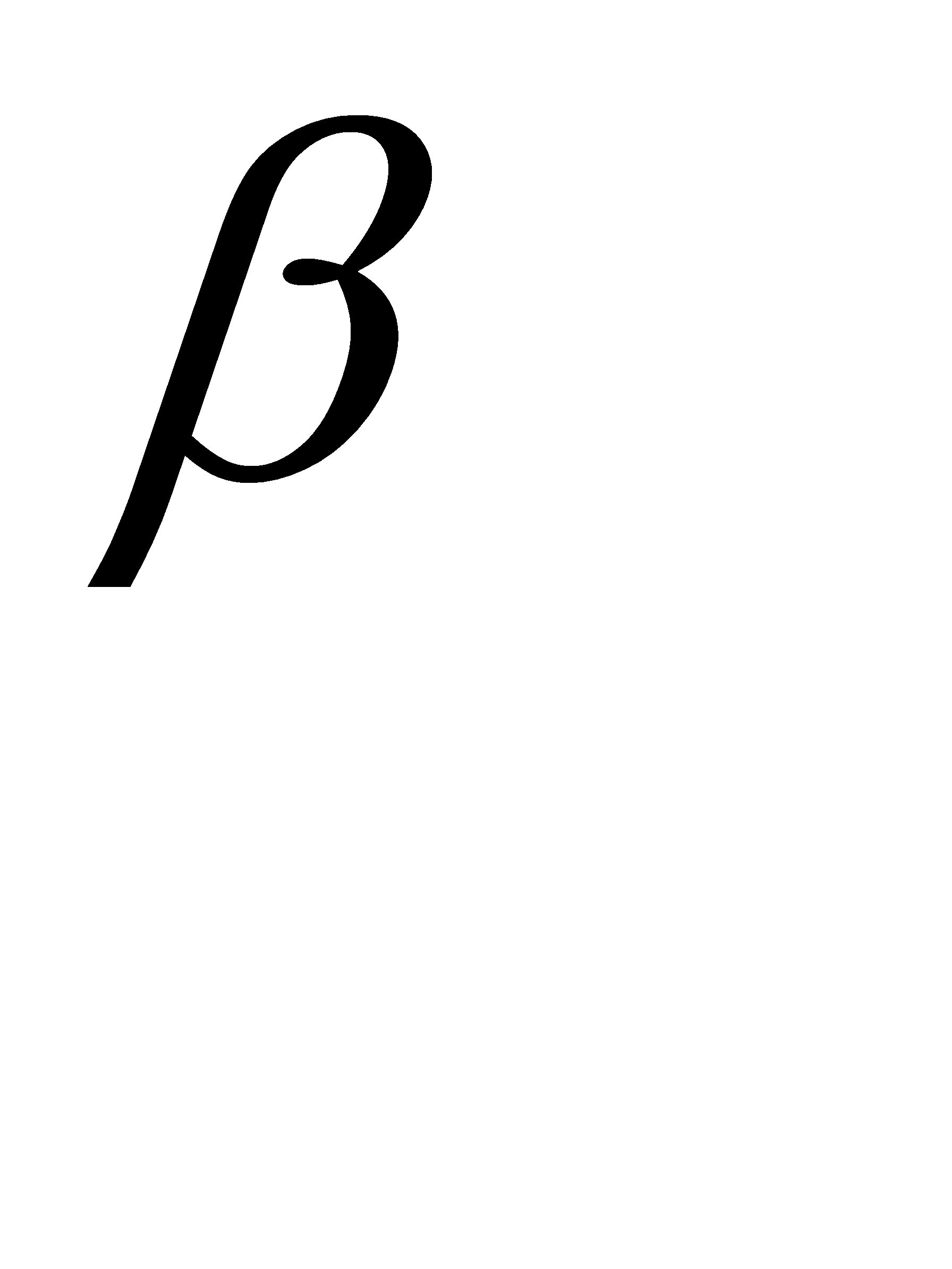
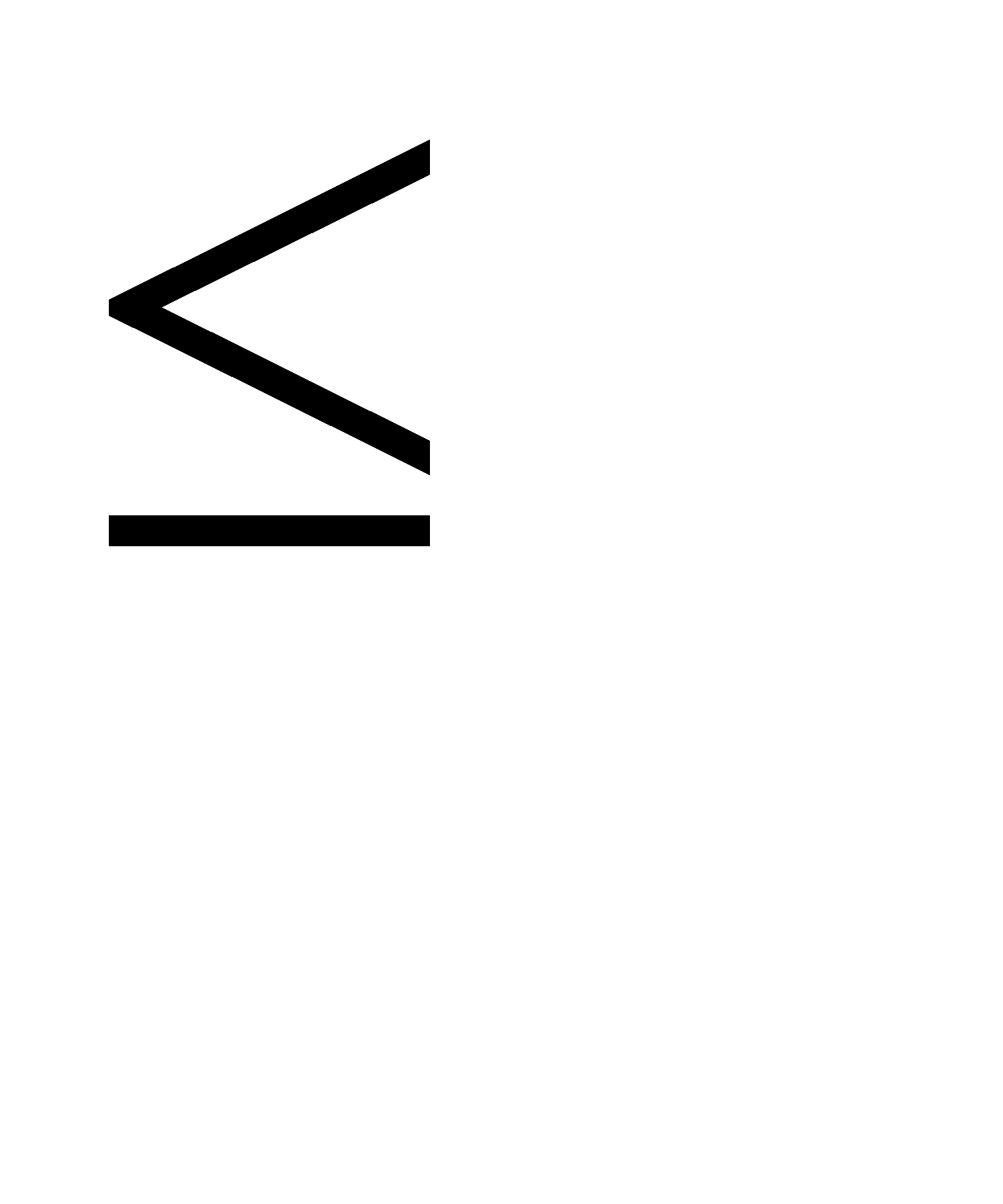 G
G 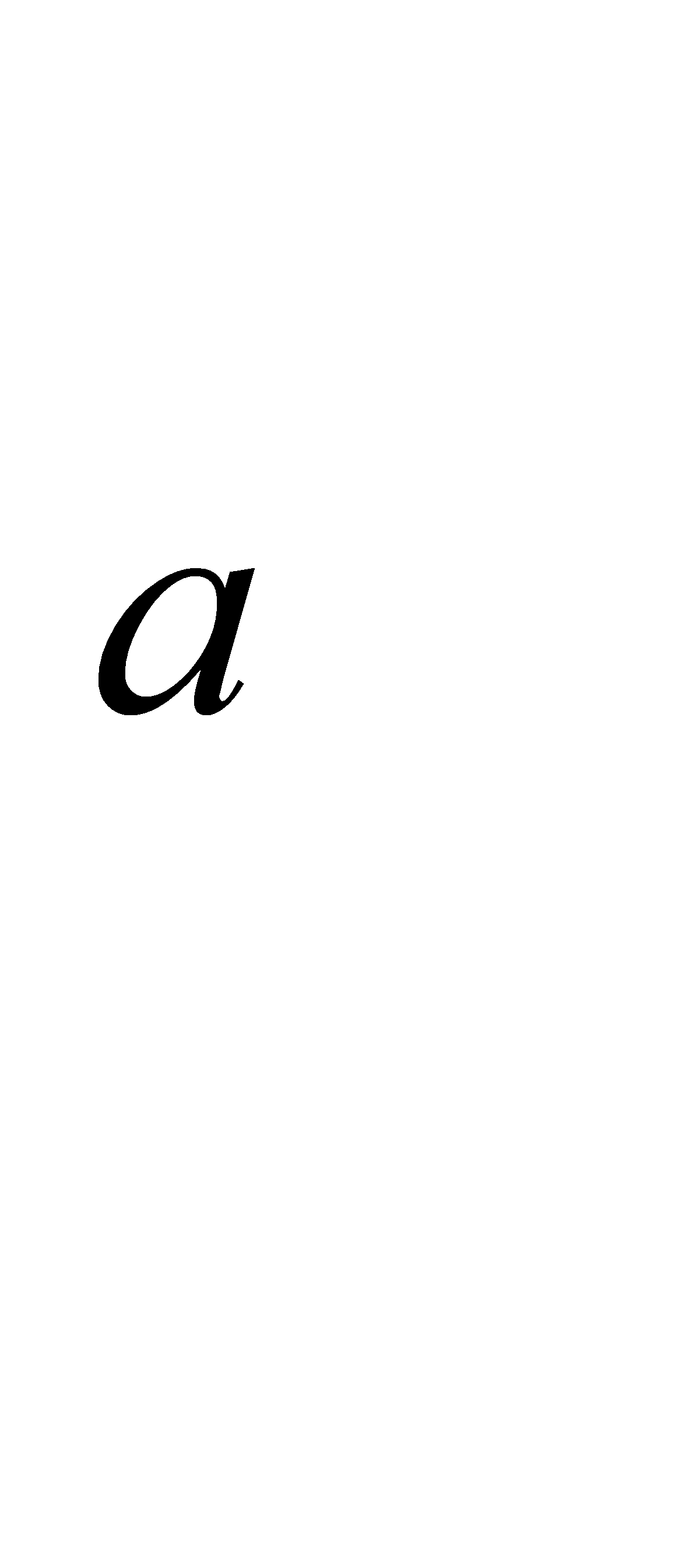 sin
sin 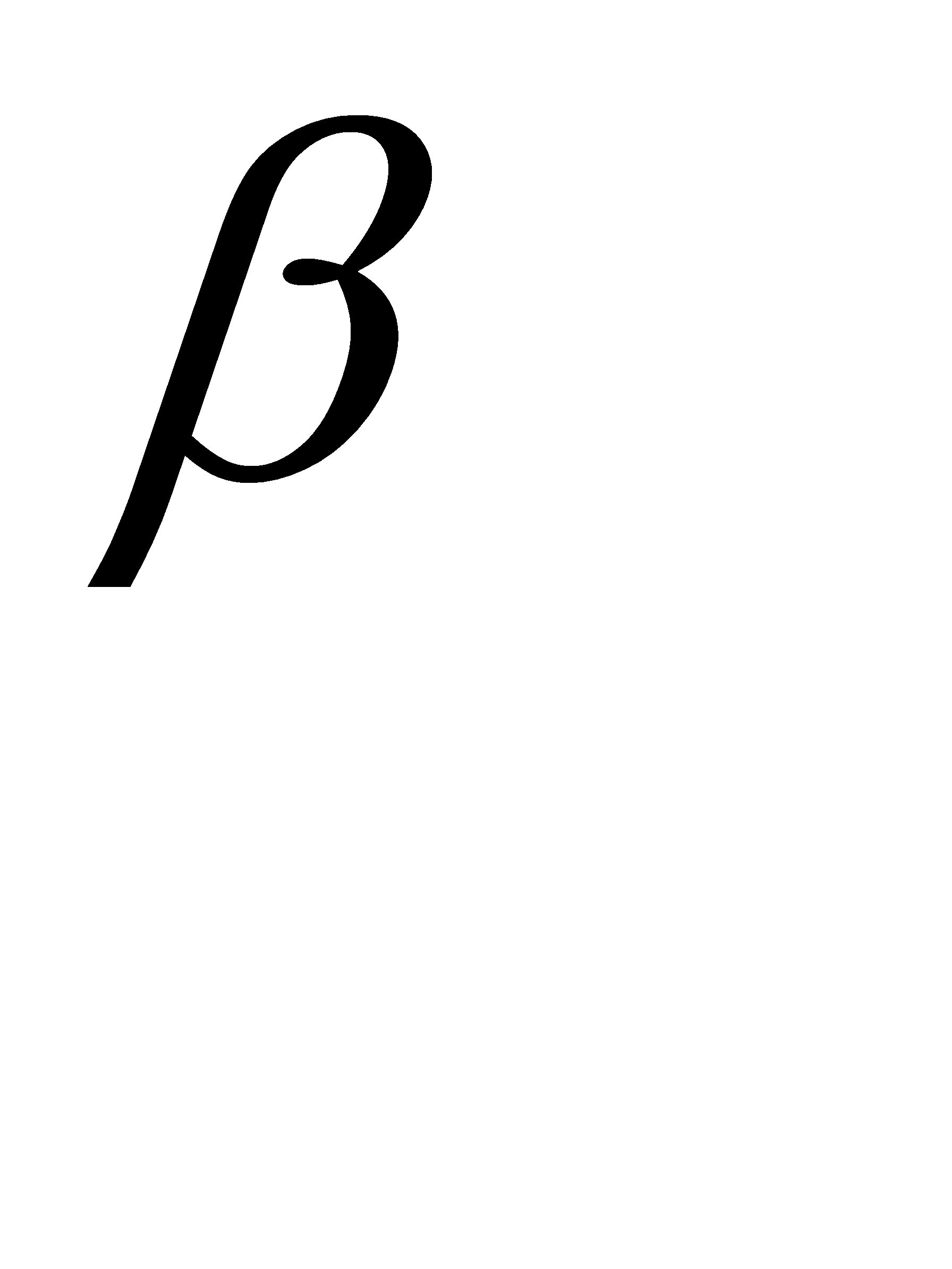 , то увеличивается опасность опрокидывания в сторону действия составляющей силы тяжести G
, то увеличивается опасность опрокидывания в сторону действия составляющей силы тяжести G 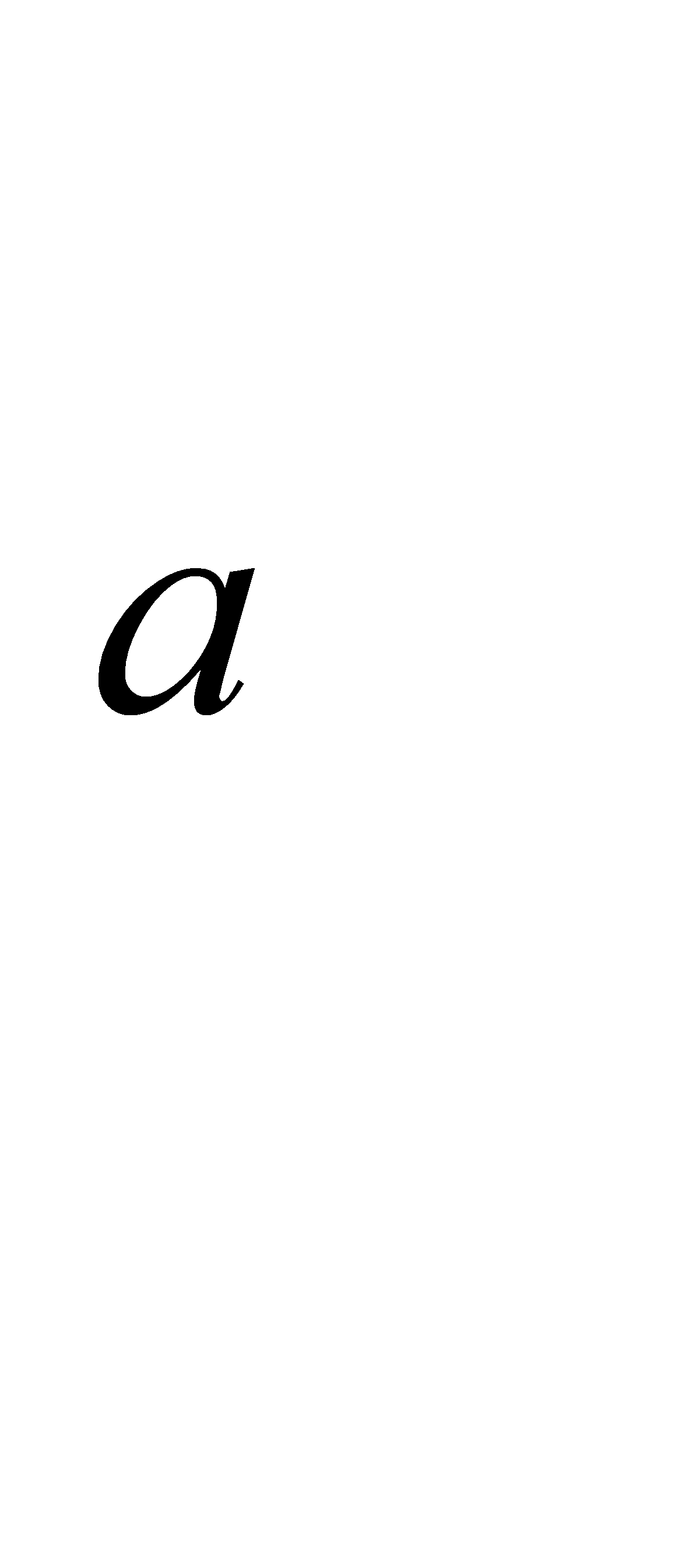 sin
sin 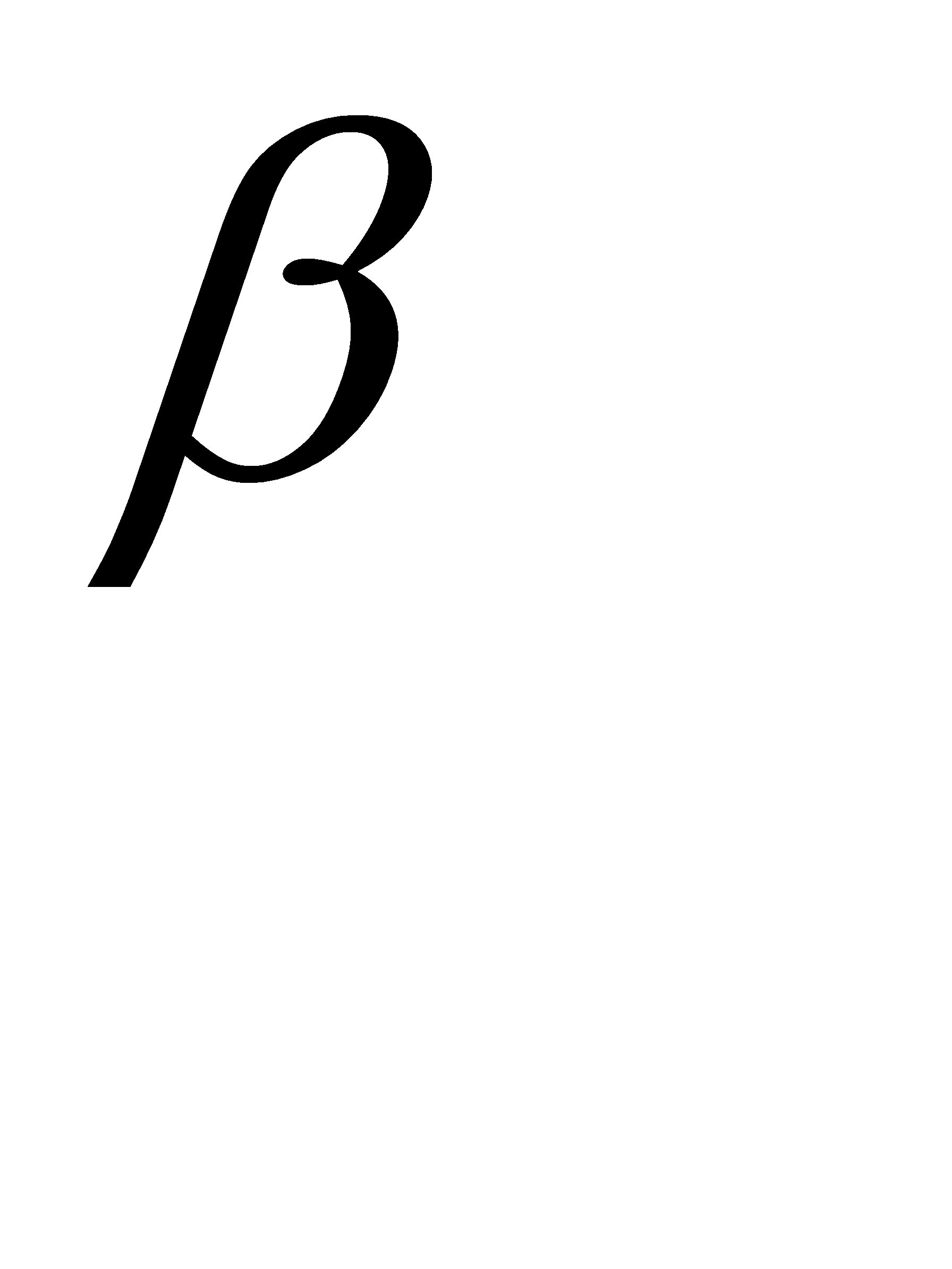 тем больше, чем меньше скорость и больше угол косогора. Решая равенство относительно
тем больше, чем меньше скорость и больше угол косогора. Решая равенство относительно 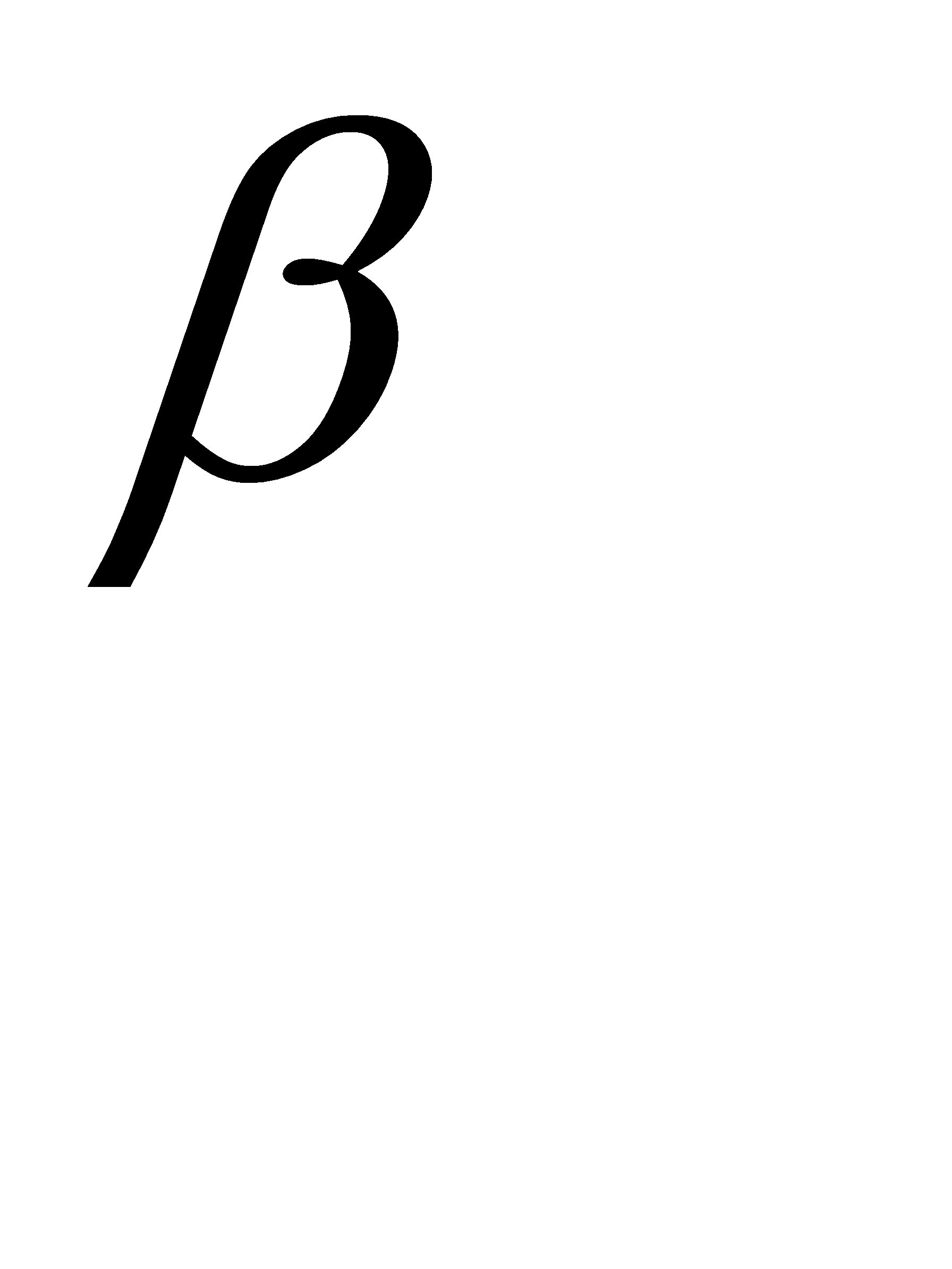 , имеем:
, имеем:
 = arctg
= arctg 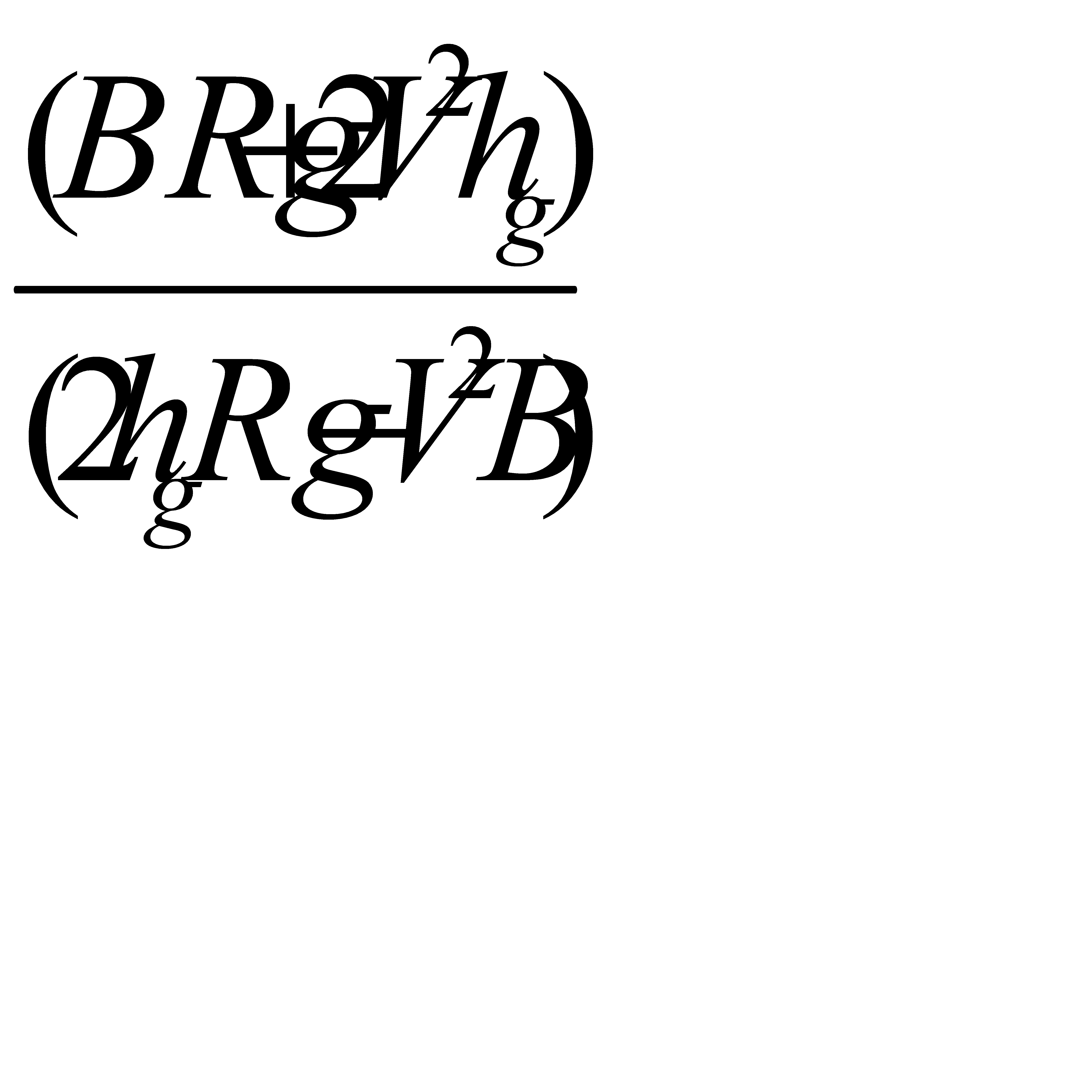 , (4.10)
, (4.10)
Минимальное значение  = arctg B/2h
= arctg B/2h 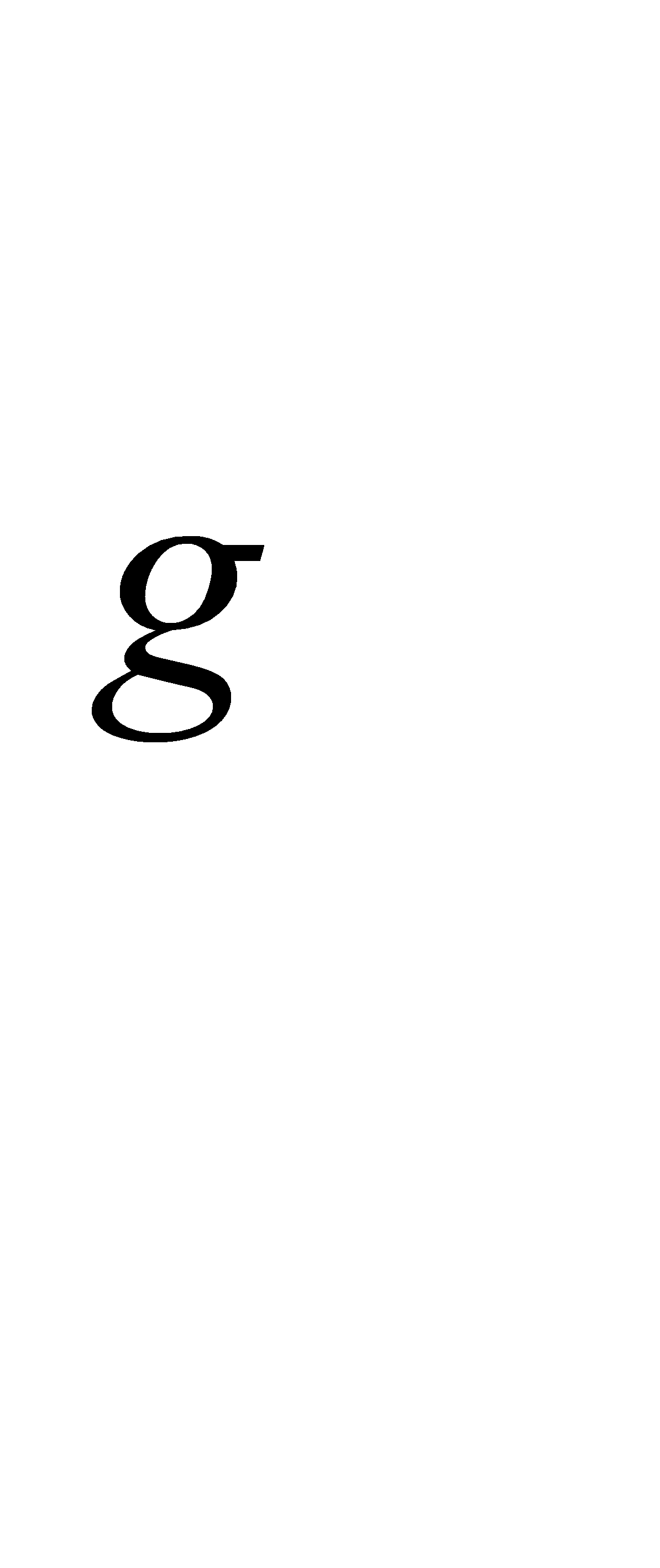 , (4.11)
, (4.11)
Следует отметить, что полученные выражения критических параметров не учитывают наклона кузова, т.е углов крена. Если при каких либо возмущениях, меняется крен кузова, то это приводит к уменьшению плеча m и увеличению h 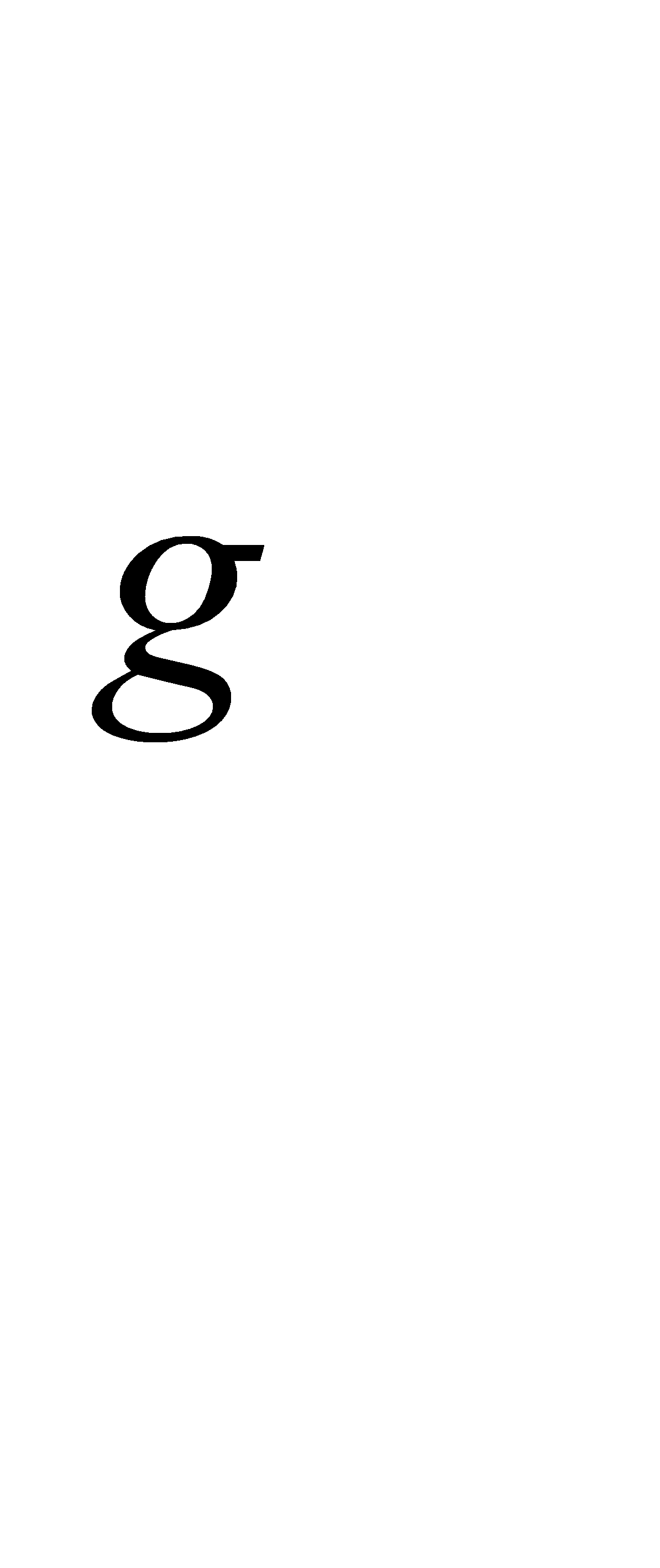 , что в свою очередь увеличивает вероятность опрокидывания даже до достижения критических параметров, рассчитываемых по полученным ранее формулам. В принципе водитель может вмешаться в развитие процесса, пока опрокидывание происходит не очень быстро, уменьшив силу Р
, что в свою очередь увеличивает вероятность опрокидывания даже до достижения критических параметров, рассчитываемых по полученным ранее формулам. В принципе водитель может вмешаться в развитие процесса, пока опрокидывание происходит не очень быстро, уменьшив силу Р  , снизив скорость или увеличив радиус.
, снизив скорость или увеличив радиус.
Из формул видно, что наличие виража повышает критические скорости. Это обстоятельство используют для повышения устойчивости движения на автомобильных дорогах. В России устраивают виражи на всех кривых с R  3000 м на дорогах первой категории и на кривых с R
3000 м на дорогах первой категории и на кривых с R  2000 м – на остальных дорогах. Обычно угол виража не превышает 6
2000 м – на остальных дорогах. Обычно угол виража не превышает 6  .
.
При проектировании АТС за счет конструктивных соотношений обеспечивают выполнение условия V 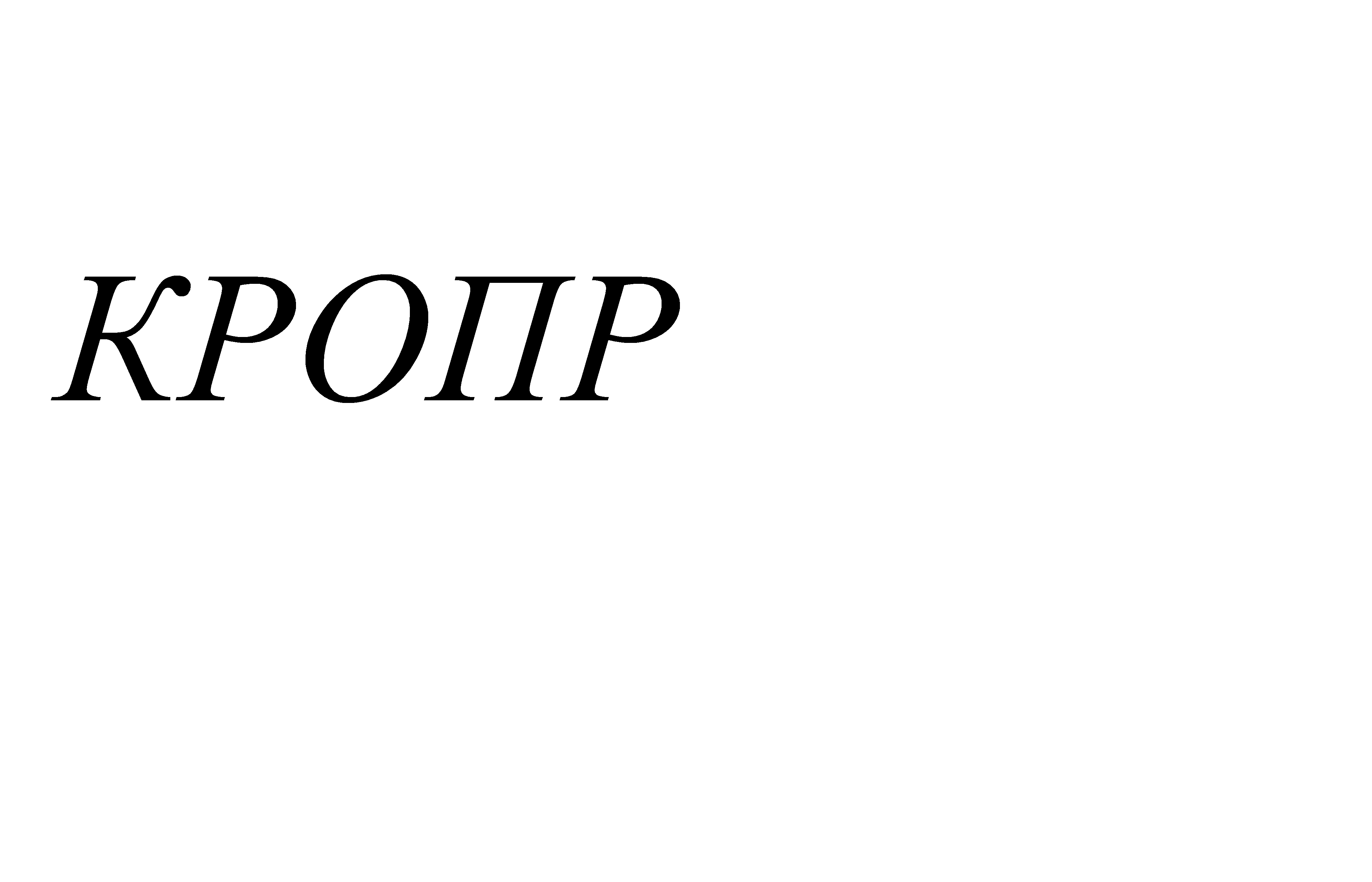

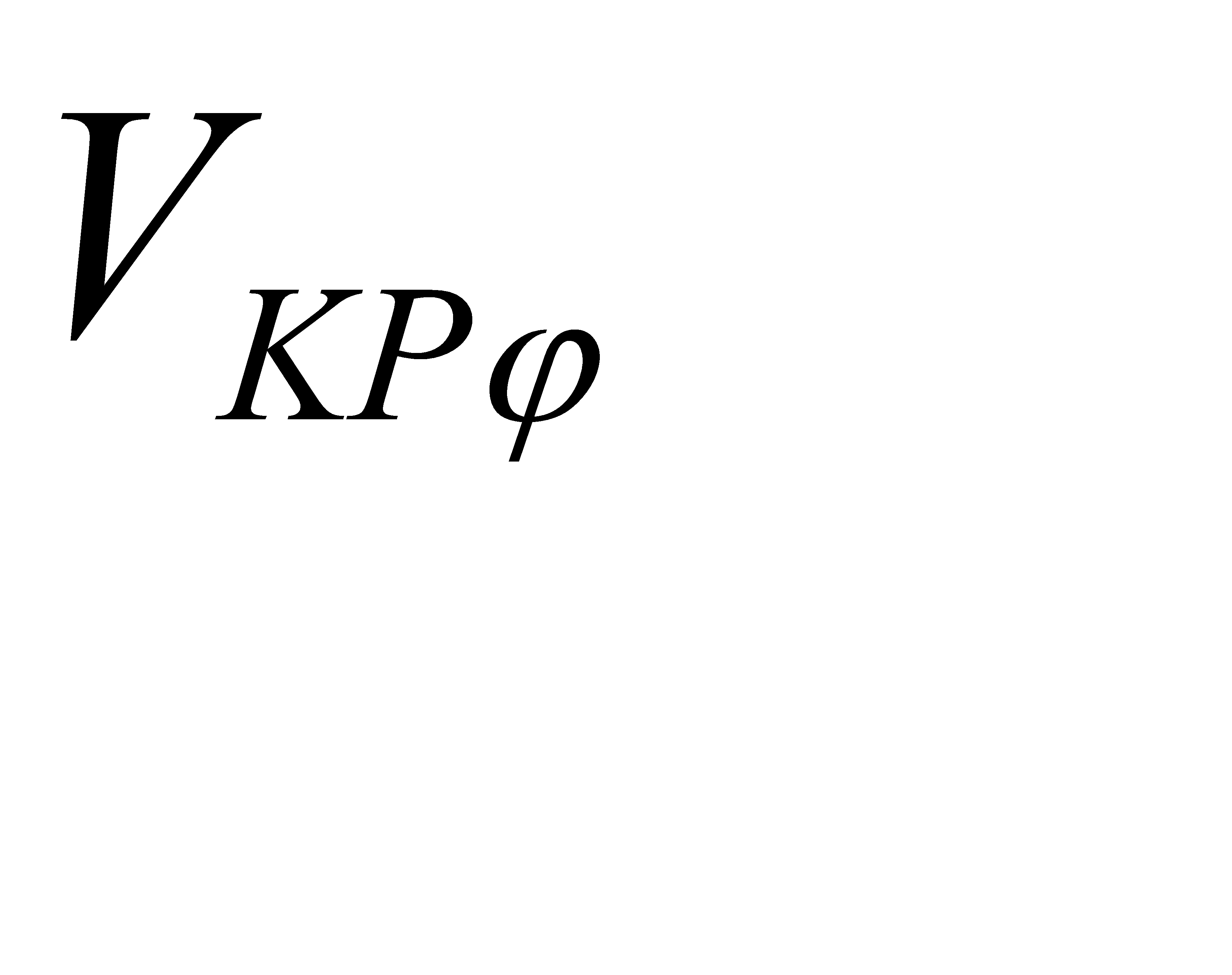 , которое иллюстрируется графиком зависимости критических скоростей (рис. 9).
, которое иллюстрируется графиком зависимости критических скоростей (рис. 9).
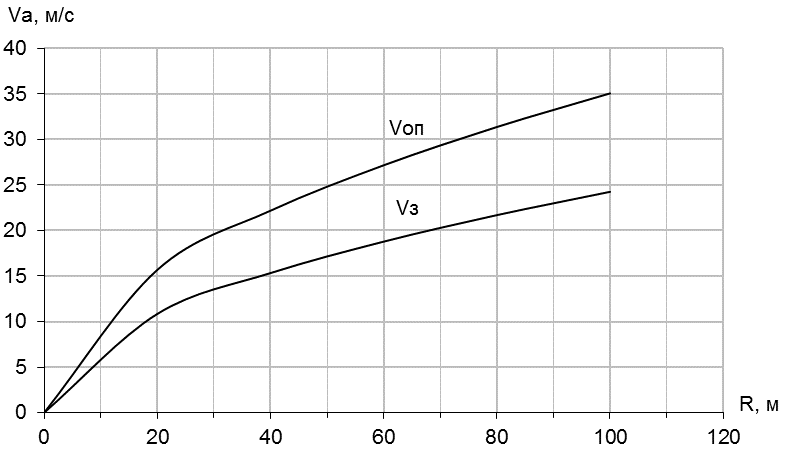
Рис. 9 График зависимости критических скоростей движения
от радиуса поворота
Дата добавления: 2021-12-14; просмотров: 595;











