Векторный момент пары сил
Векторным моментом пары сил назовем вектор, числовое значение которого равно произведению силы пары на ее плечо.
Векторный момент пары направлен перпендикулярно плоскости действия пары сил так, чтобы с его направления можно было видеть стремление пары сил вращать тело против хода часовой стрелки (рис.4.2). Векторный момент пары обозначим 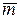 .
.
Согласно определению, числовое значение векторного момента пары 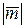 совпадает с модулем алгебраического момента пары сил, и, следовательно,
совпадает с модулем алгебраического момента пары сил, и, следовательно, 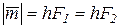 , где h – плечо пары сил. Покажем справедливость этого выражения.
, где h – плечо пары сил. Покажем справедливость этого выражения.
Векторный момент пары сил выражается в виде векторного произведения двух векторов:
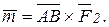 (4.2) (4.2)
| 
|
| Рис.4.2 |
Действительно,
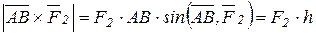 ,
,
что совпадает с модулем векторного момента пары сил.
Вектор, равный векторному произведению 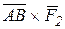 , перпендикулярен плоскости, где лежат сомножители векторного произведения и, следовательно, плоскости действия пары сил. Он совпадает с направлением векторного момента пары сил
, перпендикулярен плоскости, где лежат сомножители векторного произведения и, следовательно, плоскости действия пары сил. Он совпадает с направлением векторного момента пары сил 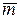 .
.
4.3. Теорема об эквивалентности двух пар сил, расположенных
в одной плоскости
Две пары сил называются эквивалентными, если их действие на твердое тело одинаково.
| Теорема. Две пары сил, расположенные в одной плоскости, эквивалентны, если они имеют одинаковые алгебраические моменты.
Докажем это утверждение. Пусть на твердое тело действует пара сил 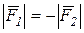 с алгебраическим моментом с алгебраическим моментом 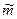 =- =- 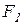 d (рис.4.3).
Перенесем силу d (рис.4.3).
Перенесем силу 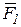 в точку О1, а силу в точку О1, а силу 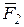 в точку О2, проведем через точки О1 и О2 соответственно две любые параллельные прямые в точку О2, проведем через точки О1 и О2 соответственно две любые параллельные прямые 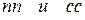 , пересекающие линии действия сил пары и лежащие в плоскости действия заданной пары сил. , пересекающие линии действия сил пары и лежащие в плоскости действия заданной пары сил.
|
| Рис.4.3 |
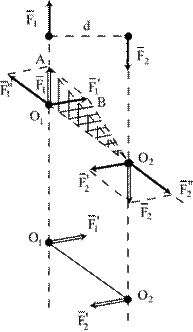
Соединив прямой точки О1 и О2, разложим силы по правилу параллелограмма по выбранным направлениям, как указано на рис.4.3.
Тогда 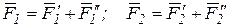 .
.
Так как силы 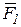 и
и 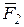 образуют пару сил, то
образуют пару сил, то 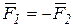 и, следовательно,
и, следовательно, 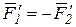 ,
, 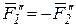 . Так как
. Так как 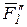 и
и 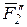 лежат вдоль одной линии действия, они образуют систему сил, эквивалентную нулю, следовательно, эту систему двух сил можно отбросить.
лежат вдоль одной линии действия, они образуют систему сил, эквивалентную нулю, следовательно, эту систему двух сил можно отбросить.
Таким образом, заданную пару сил с алгебраическим моментом 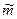 заменяем другой парой с алгебраическим моментом
заменяем другой парой с алгебраическим моментом 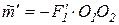 . Докажем, что алгебраические моменты у этих пар одинаковы, т.е.
. Докажем, что алгебраические моменты у этих пар одинаковы, т.е. 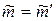 . Направление вращения у них одно и то же. Площади треугольников О1О2А и О1О2В обозначим соответственно через А1 и А2, тогда
. Направление вращения у них одно и то же. Площади треугольников О1О2А и О1О2В обозначим соответственно через А1 и А2, тогда
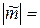 2А1,
2А1, 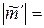 2 А2.
2 А2.
Но А1 = А2, так как эти треугольники имеют общее основание О1О2 и равные высоты. Следовательно, 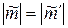 . Теорема доказана.
. Теорема доказана.
Сформулируем следующие выводы:
· пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия;
· у пары сил можно изменять плечо силы, сохраняя при этом алгебраический момент пары и плоскость действия.
Дата добавления: 2019-12-09; просмотров: 1374;











