Распределенные силы

В статике рассматривают силы, приложенные к твердому телу в какой-либо его точке. Такие силы называют сосредоточенными.

В действительности силы бывают приложены к какой-либо части тела. Так как все аксиомы и теоремы статики формулируются для сосредоточенных сил, приложенных к твердому телу, то необходимо рассмотреть способы перехода от распределенных сил к сосредоточенным в простейших, наиболее часто возникающих случаях.

Распределенные силы характеризуются в каждой точке числовым значением и направлением вектора интенсивности этой нагрузки.

Интенсивность может быть отнесена к единице объема (Н/м³), единице площади (Н/м²) или единицы длины (H/м). Соответственно распределенная сила будет называться объемной (рис.3.4а), поверхностной (рис.3.4б) и линейно распределенной (рис.3.4в).

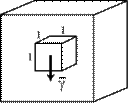
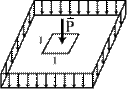
а				в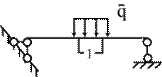
Рис.3.4

Распределенную нагрузку можно понимать как силу, приходящуюся соответственно на единицу объема, площади и длины. Линейно распределенная нагрузка постоянной интенсивности называется равномерно распределенной нагрузкой.

Рассмотрим пример равномерно распределенной нагрузки. Пусть участок АВ (рис.3.5а), длина которого L, нагружен равномерно распределенной нагрузкой. Разобьем АВ на отрезки достаточно малых размеров по сравнению с его длиной. На каждый такой малый отрезок действует сила 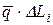. Эту силу при достаточно малой длине отрезка 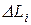можно считать сосредоточенной силой. Заменяя полученную таким образом систему сосредоточенных параллельных сил одной равнодействующей силой, получим (рис.3.5б)

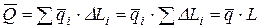. (3.6)

Равнодействующая 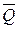направлена параллельно распределенным силам и приложена вследствие симметрии распределения сил в середине отрезка АВ.

а     б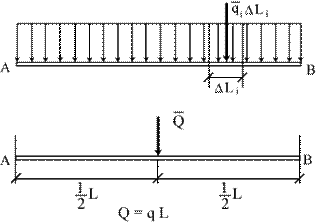
Рис.3.5

Рассмотрим распределенные параллельные силы, интенсивность которых

меняется по линейному закону (рис. 3.6а). Обычно называют, что такие силы распределены по треугольнику. Определим равнодействующую. Наиболее просто это можно сделать путем интегрирования. Действительно,

.

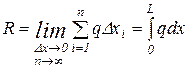Если х отсчитывать от точки А, то из подобия треугольников имеем:

.

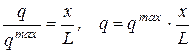Подставив в интеграл значение q, получим:

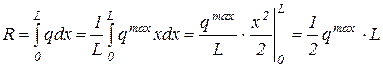. (3.7)

а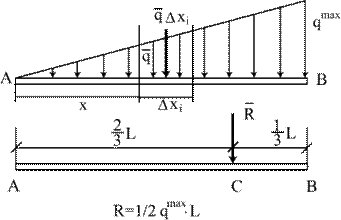
б
Рис.3.6

Точка приложения С равнодействующей силы смещается в сторону, где интенсивность силы больше, и совпадает с положением центра тяжести треугольника, который находится в точке пересечения медиан. В данном случае линия действия равнодействующей 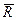проходит через точку С, расположенную на 2L/3 от вершины А и на L/3 от основания треугольника, т.е. АС = 2L/3, а СВ=L/3 (рис.3.6).

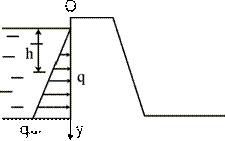
	Примером треугольно распределенной нагрузки может служить давление жидкости на плотину, изменяющееся с глубиной по закону q(y) =ky (рис.3.7).
Рис.3.7

Итак, распределенная нагрузка характеризуется равнодействующей, величина которой в общем случае равна

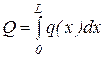. (3.8)

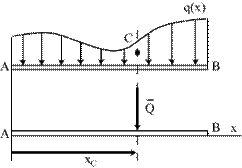
Линия действия равнодействующей 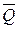параллельна распределенным силам и проходит через центр тяжести этой площади (рис.3.8). Вопрос об определении центров тяжести площадей будет рассмотрен в лекции 10.
	Рис.3.8

Величину равнодействующей в случае непараллельных распределенных сил находят так же, как и для параллельных, только суммируют (и, следовательно, интегрируют) не элементарные сосредоточенные силы, а их проекции на оси координат. По проекциям уже вычисляют равнодействующую силу и косинусы ее углов с осями координат.