Приведение к равнодействующей двух сил, направленных в одну сторону

Рассмотрим сначала систему двух параллельных сил, направленных в одну сторону. Так как силу можно переносить в любую точку линии ее действия, то достаточно знать только линию действия силы и ее модуль, а за точку приложения можно брать любую точку линии действия силы.

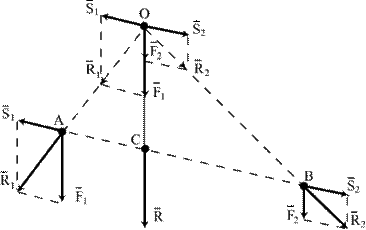
Определим равнодействующую системы двух параллельных сил (рис. 3.1). Для этого систему параллельных сил сведем к системе сходящихся сил.

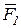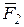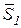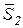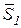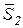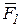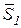Пусть имеем две параллельные силы, направленные в одну сторону, и . Соединим точки приложения данных сил отрезком АВ. В точках приложения А и В приложим две равные по модулю силы и , направленные по отрезку АВ в противоположные стороны (силы и составляют систему сил, эквивалентную нулю). Теперь сложим силы и 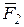, и и 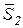, получим их равнодействующие 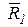и .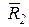

Рис.3.1

Продолжим линии действия сил 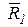и 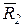до их пересечения в точке О и перенесем 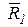и 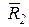в эту точку. Теперь каждую силу 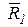и 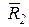разложим по правилу параллелограмма на составляющие силы 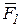, 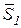и 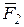, , 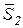параллельные прямой АВ и силам 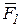и .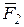

Систему сил 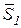и 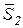, как эквивалентную нулю, отбросим. Тогда останутся две силы: 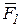и 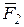. Эти силы направлены в одну сторону и действуют по одной прямой, которая параллельна линиям действия сил 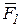и 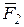. Следовательно, равнодействующая эти сил будет равна их алгебраической сумме:

R=F₁ + F₂ (3.1)

и направлена параллельно данным силам. Из подобия треугольников АОС, R₁OF₁, COB и F₂OR₂ имеем:

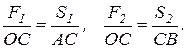(3.2)

Разделив одну пропорцию на другую, получим

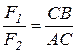, откуда 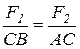. (3.3)

Таким образом, точка С находится на отрезке АВ и делит его на части, обратно пропорциональные силам.

Сложим пропорции (3.2):

.

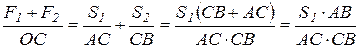Перепишем эту пропорцию удобно для дальнейших вычислений. Выразим значение S₁ через F₁ и F₂ из (3.2). Получим, имея в виду, что

F₁ + F₂ = R; ; ,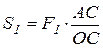

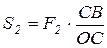следующее выражение:

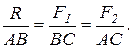(3.4)

Из последнего равенства легко определить отрезки АС и ВС.

Если на тело действует несколько параллельных сил, то их равнодействующую можно найти, последовательно применяя правила сложения двух сил. Если система параллельных сил находится в равновесии, то равнодействующая должна быть равна нулю.