Приведение к равнодействующей двух сил, направленных в разные стороны
Рассмотрим сложение двух сил, направленных в разные стороны. Пусть имеем две силы 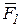 и
и 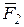 (F2>F1) (рис.3.2а). Возьмем на продолжении прямой ВА точку С и приложим к ней уравновешенные силы
(F2>F1) (рис.3.2а). Возьмем на продолжении прямой ВА точку С и приложим к ней уравновешенные силы 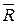 и
и 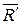 , параллельные силам
, параллельные силам 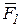 и
и 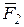 (рис.3.2б).
(рис.3.2б).
| а | 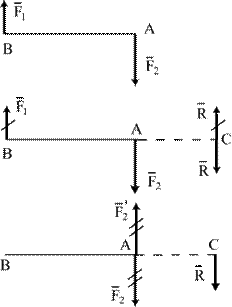
| При этом модуль 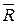 и положение точки С должны удовлетворять уравнению (3.4): и положение точки С должны удовлетворять уравнению (3.4):
 , , 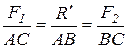 . (3.5)
Сложим силы . (3.5)
Сложим силы 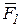 и и 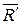 . Получим, что их равнодействующая . Получим, что их равнодействующая  равна по модулю равна по модулю 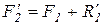 , т.е. равна по модулю F2 и приложена в точке А.
После этого силы , т.е. равна по модулю F2 и приложена в точке А.
После этого силы 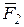 и и  можно можно
|
| б | ||
| в | ||
| Рис.3.2 |
отбросить как уравновешенные. В результате заданные силы 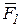 и
и 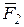 будут заменены одной силой
будут заменены одной силой 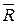 , которая является их равнодействующей. Модуль этой равнодействующей и точка ее приложения С определяются по формулам (3.5) (рис.3.2в).
, которая является их равнодействующей. Модуль этой равнодействующей и точка ее приложения С определяются по формулам (3.5) (рис.3.2в).
Пример. Определить реакции опор в шарнирно - опертой балке АВ, показанной на рис. 3.3а. Дано: Р=9кН, а=6м, b=12м.
Решение. Отбросим связи и заменим их реакциями (рис. 3.3б). Реакция шарнирно - подвижной опоры 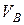 направлена параллельно линии действия внешней силы Р, следовательно, их уравновешивающая сила
направлена параллельно линии действия внешней силы Р, следовательно, их уравновешивающая сила  должна быть им параллельна. Согласно (3.5), имеем
должна быть им параллельна. Согласно (3.5), имеем
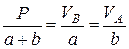 ,
,
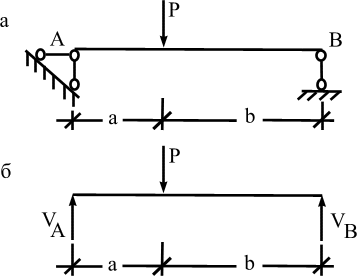
Рис. 3.3
откуда
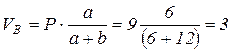 кН,
кН,
 кН.
кН.
Сделаем проверку. Балка АБ находится в равновесии, следовательно, равнодействующая системы параллельных сил должна быть равна нулю:
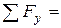
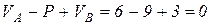 .
.
Дата добавления: 2019-12-09; просмотров: 754;











