Структурный анализ механизма щековой камнедробилки

На рис.2.1 показана схема механизма камнедробилки, который может быть определен как плоский рычажный механизм, поскольку его звенья движутся в параллельных плоскостях, и эти звенья объединены в кинематическую цепь низшими кинематическими парами. Согласно приведенной выше последовательности решения задач структурного анализа определяем следующее.

1) Данный механизм образован пятью подвижными звеньями и стойкой, объединенными в замкнутую кинематическую цепь семью кинематическими парами. Подвижные звенья обозначаем цифрами от 1 до 5; стойку обозначаем цифрой 0;

кинематические пары обозначаем прописными буквами латинского алфавита (см. рис. 2.1).Отмечаем, что буквой С обозначены две кинематические пары, одна из которых определяется как соединение звеньев 2и 3, другая — как соединение звеньев 3 и 4.

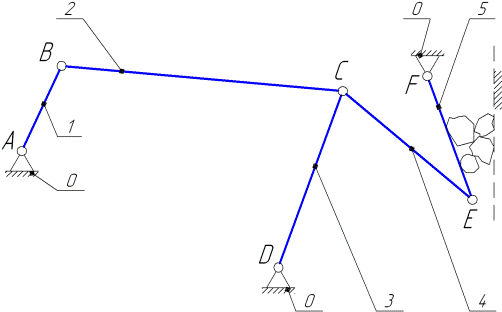
Рис.2.1

2) Все кинематические пары механизма допускают только вращательное относительное движение звеньев, поэтому классифицируются как вращательные кинематические пары V класса.

3) Движение звена 1 определяется как вращательное вокруг неподвижной оси с поворотом за цикл работы механизма на 360 градусов; звено 2 совершает плоское движение: звено не имеет неподвижных точек и меняет направление своей оси наплоскости; звено 3 совершает вращательное движение вокруг неподвижной оси с поворотом на угол меньше 360 градусов в обоих направлениях; звено 4 движется аналогично звену 2; звено 5 движется также, как звено 3. Исходя из вида движения каждого звена и в соответствии с принятой в ТММ терминологией звено 1 определим как кривошип, звенья 2 и 4 — как шатуны, звенья 3 и 5 — как коромысла.

4) Число степеней свободы (подвижность) механизма определим по структурной формуле П.Л.Чебышева для плоских механизмов:

,

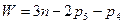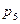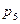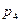где п— число подвижных звеньев механизма (п = 5); — число кинематических пар V класса ( = 7); — число кинематических пар IV класса ( 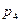= 0).

Выполняем расчет: .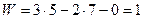

Таким образом, подвижность механизма равна единице. Отсюда следует, что движение всех звеньев механизма будет вполне определенным, если одному из этих звеньев сообщить некоторый закон движения. Это звено оказывается в результате начальным (или входным), а координата, с помощью которой отсчитывается его движение, — обобщенной координатой механизма, функциями которой можно описывать движение остальных звеньев.

5) Обычно в качестве входных звеньев принимаются звенья, образующие кинематические пары со стойкой и совершающие простые движения — поступательное или вращательное. В этом случае сообщить звену заданный закон движения технически проще. По этой причине в рассматриваемом механизме входным звеном выгодно назначить кривошип, поскольку закон движения такому звену можно сообщить при помощи обычного механизма передачи вращения или непосредственно от двигателя (электрического, внутреннего сгорания и т.п.). Таким образом, в заданном механизме в качестве входного звена выбираем кривошип 1, соответственнообобщенной координатой механизма будет угол поворота этого кривошипа.

6) Устанавливаем, что структура заданного механизма соответствует основному принципу образования плоских механизмов, состоящему в последовательном присоединении к ведущим звеньям и стойке (механизмам I класса) групп звеньев нулевой подвижности (групп Ассура). Согласно этому принципу выделяем кривошип 1 и стойку 0 — механизм I класса (см. рис.2.2, а). Затем выделяем пару звеньев 2,3 — группу II класса второго порядка первого вида (см. рис.2.2, б); эта группа в кинематической пареВ присоединена к кривошипу 1 и в паре D— к стойке 0. Далее выделяем пару звеньев 4,5 — группу IIкласса второго порядка первого вида (см.рис.2.2, в); эта группа в кинематической паре С присоединена к звеньям 2,3 и в паре F— к стойке 0.

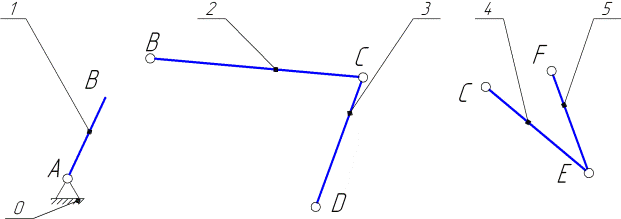
а) б) в)

Рис. 2.2

7) Формула строения механизма, исходя из предыдущего, следующая:

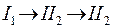
8) В заданный механизм входят группы класса не выше второго, поэтому механизм классифицируется как механизм IIкласса.