Материальный баланс массообмена. Рабочая линия.

Рабочие концентрации распре­деляемого вещества не равны равновесным, и в действующих аппаратах никогда не достигают равновесных значений.

Зависимость между рабочими концентрациями, распределяемого ве­щества в фазах Y = f(X) изображается линией, которая носит название рабочей линии

Процесса.

Вид функции Y = f(X) или уравнение рабочей линии в его общем виде, является одинаковым для всех массообменных процессов и получается из их материальных балансов.

Рассмотрим схему массообменного аппарата, работающего в режиме идеального вытеснения при противотоке фаз (рисунок 3.2). Пусть в процессе массопередачи из фазы в фазу, например из газовой фазы в жидкую, пе­реходит только один распределяемый компонент.

Сверху в аппарат поступает Lн кг/сек одной фазы (жидкой), содержа­щей Хн массовых долей распределяемого компонента, а снизу из аппарата удаляется Lк кг/сек той же фазы, содержащей Хк массовых долей распределяе­мого компонента. Снизу в аппарат поступает Gн кг/сек другой фазы (газо­вой) концентрацией Уни сверху удаляется Gк кг/сек этой фазы, имеющей концентрацию Укмассовых долей распределяемого компонента.

Тогда материальный баланс по всему веществу

Gн + Lн = Lк + Gк (3.4)

и материальный баланс по распределяемому ком­поненту

Gн× Ун + Lн× Хн = Lк× Хк + Gк× Ук (3.5)

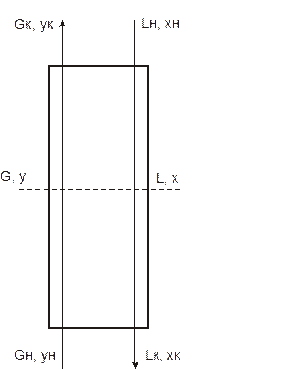
Рисунок 3.2. К выводу уравнения материального баланса противоточного массообменного аппарата

Уравнение материального балан­са для части аппарата от его нижнего конца до неко­торого произвольного сечения, для которого расхо­ды фаз составляют G и L кг/сек, а их текущие кон­центрации равны Уи Хсоответственно.

Материальный баланс по всему веществу

Gн + L = Lк + Gк (3.6)

и материальный баланс по распределяемому ком­поненту

Gн× Ун + L× Х = Lк× Хк + G× У (3.7)

Решая это уравнение относительно У, получим

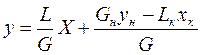(3.8)

Уравнение (3.8) представляет собой уравнение рабочей линии, выражающее связь между рабочими концентрациями распреде­ляемого компонента в фазах для произвольного сечения аппарата.

Если концентрации фаз мало изменяются по высоте аппарата, то расходы фаз по его высоте можно с достаточной для практических целей точностью считать постоянными, т. е. принять L = const и G = const. В этом случае уравнение (3.8 ) приходит к виду:

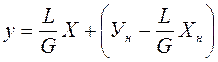(3.9)

Вводя обозначения 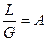и 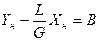, получаем уравнение прямой линии:

У = А×Х +В

Таким образом, рабочая линия представляет собой прямую, которая наклонена к горизонту под углом, тангенс которого равен А, и отсекает на оси ординат отрезок, равный В. Рабочая линия для всего аппарата ограничена точками с координатами Хн и Ук(верхний конец аппарата, рисунок 3.2) и Ук и Хн(нижний конец аппарата).

Если расходы фаз значительно изменяются по высоте ап­парата, то материальные балансы по компоненту- носителю для части аппарата от его нижнего конца до произвольного сечения (где концентрации фаз равны Х и У) выражаются уравнениям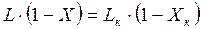и:

и 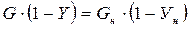(3.10)

откуда

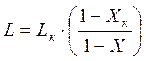и 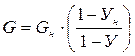(3.11)

Подставив значения L и G в общее уравнение материального баланса (3.7) и после соответствующих преобразований, получим

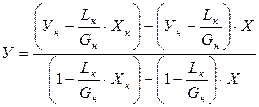(3.12)

Из уравнения полученного уравнения следует, что в рассматриваемом случае рабочая линия криво­линейна.