РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ.

Сигналы.

Под словом «сигнал» обычно понимают любые электрические колебания. В этом смысле различают следующие виды сигналов: детерминированные и случайные; аналоговые и дискретные; сигналы с амплитудной, частотной, фазовой модуляцией; узкополосные и широкополосные.

Детерминированный сигнал описывается аналитическим выражением или графиком. Его параметры можно определить в любой момент времени с точностью до 1.

Случайный сигнал не может быть описан аналитическим выражением и его параметры могут быть определены только приближенно. Случайные сигналы часто препятствуют извлечению информации из принятого колебания.

Различие детерминированных и случайных сигналов определяется возможностью или невозможностью точного предсказания их мгновенных значений в любые моменты времени.

Аналоговый сигнал описывается непрерывной функцией. Значение такого сигнала в каждый момент времени имеет смысл и несет определенную информацию.

Дискретный сигнал описывается функцией, имеющей конечное число фиксированных значений. Промежуточные значения смысла не имеют. Особой разновидностью дискретных сигналов являются цифровые сигналы. Для них отсчетные значения представлены в форме чисел

Импульсы – это колебания, существующие лишь в пределах конечного отрезка времени.

Сигналы с той или иной модуляцией (модулированные) – это сигналы, один из параметров которых меняется по закону изменения других (модулирующих) сигналов. Меняться может амплитуда, частота или фаза модулируемого колебания.

Узкополосные сигналы - это колебания сложной формы, имеющие относительно небольшую разницу между частотами нижней и высшей гармонической составляющей этого сигнала.

Широкополосные – для них разница между частотами высшей и низшей гармонической составляющей сигнала, измеряется несколькими порядками.

Задание на дом. Начертить временные диаграммы сигналов различного типа. Пояснить, почему данный сигнал так называется.

К простым сигналам, наиболее часто используемым при проведении различных испытаниях радиоаппаратуры, относятся сигналы синусоидальной и прямоугольной формы.

Простейшим сигналом является синусоидальный, который описывается следующим аналитическим выражением 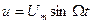, где u – мгновенное значение напряжения в данный момент времени; Uт – амплитудное значение напряжения; Ω – круговая частота ; t – время. Синусоидальный сигнал (Рис. 8) симметричен относительно оси времени и не содержит постоянной составляющей. Этот сигнал характеризуется следующими величинами:

Um- амплитудное значение напряжения;

U- действующее значение напряжения;

T-период колебания;

f- частота колебания;

φ-начальная фаза колебания.

Рис. 8. Временная диаграмма синусоидального сигнала.

Для синусоидального колебания амплитуда положительного полупериода равна амплитуде отрицательного полупериода. Сумма амплитудных значений положительного и отрицательного полупериодов (без учёта знаков) называется двойной амплитудой или размахом напряжения. Действующее значение напряжения 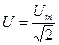. Среднее значение напряжения равно нулю. Период и частота связаны следующим выражением или 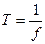. В том случае, когда синусоидальный сигнал является электромагнитным колебанием, т.е. радиоволной, то он характеризуется длиной волны 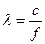, где c - скорость распространения волны. Для воздуха c 300000 км/с.

Сигнал прямоугольной формы может быть симметричным относительно оси времени (Рис.9а) или представлять собой импульсы одной полярности напряжения (Рис.9б).

Рис. 9. Временные диаграммы сигналов прямоугольной формы. а) симметричный сигнал, не имеющий постоянной составляющей, б) однополярный сигнал.

Если сигнал прямоугольной формы симметричен относительно оси времени, то постоянная составляющая сигнала равна нулю. В противном случае в сигнале присутствует постоянная, составляющая U₀, величина которой зависит от скважности 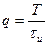, где T – период, τ_и – длительность импульса. Если скважность равна 0,5, т.е. τ _u = 0,5T, то такой сигнал называется, меандром. Итак, сигнал прямоугольной формы характеризуется следующими величинами:

Um- амплитуда импульса (уровень напряжения);

T-период повторения импульсов;

f- частота повторения импульсов;

τ _u – длительность импульса;

q- скважность импульса.

Периодические сигналы синусоидальной и прямоугольной формы относятся к детерминированным сигналам и никакой полезной информации не передают. Для того, чтобы эти сигналы передавали какую- либо полезную информацию необходимо менять один из параметров этих колебаний. Например, синусоидальный сигнал может меняться по амплитуде, частоте и фазе, а прямоугольный - по частоте, длительности импульса, скважности, уровню напряжения.

Среди различных сигналов прямоугольной формы выделяются одиночные импульсы, период следования которых не является величиной постоянной. Такие сигналы относятся к случайным сигналам.

Сложный сигнал представляет собой совокупность простых синусоидальных колебаний, имеющих различные значения частоты и амплитуды.

Совокупность простейших (синусоидальных) составляющих сложного колебания образует его спектр, а составляющие называются гармониками.

В зависимости от особенностей сигнала, его спектр может быть сплошным (одиночный импульс) или дискретным (линейчатым) для гармонических сигналов.

При сложении нескольких (в простейшем случае двух) простых колебаний результат может быть различным.

Если два синусоидальных колебания воздействуют на линейную систему, то в результате получается гармоническое колебание сложной формы, содержащее эти два исходных колебания. Гармоническое колебание любой, сколь угодно сложной, формы может быть разложено на составляющие- гармоники. Совокупность гармоник называется спектром колебания (Рис. 10).

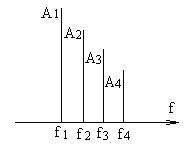
Рис. 10. Спектр сложного гармонического сигнала.

A – амплитуда гармоники, f – частота гармоники.

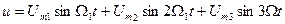+ и т.д.

Гармоники являются простыми, синусоидальными колебаниями различной амплитуды, частоты и фазы. Пример воздействия нескольких простых колебаний на линейную систему показан на рисунке 11.

Искажение формы выходного сигнала, при прохождении его через усилитель, рассматривается как появление в выходном сигнале дополнительных гармоник, не содержащихся во входном сигнале. Поэтому такие искажения называются гармоническими и оцениваются коэффициентом гармоник.

Если же два синусоидальных колебания различной частоты воздействуют на нелинейную систему, то на выходе ее появляются колебания иных частот, нежели тех, что действуют на входе системы. В этом случае один из параметров, например, амплитуда, высокочастотного колебания меняется по закону низкочастотного колебания, которое называется управляющим. В результате выходной сигнал не является синусоидальным, и состав его спектра будет иным, нежели при воздействии на линейную систему. Пример такого воздействия четырёх синусоидальных колебаний на линейную систему показан на рисунке 11.

Состав спектра сигнала может быть показан на спектральной характеристике, т.е. зависимости амплитуды гармонических составляющих от частоты. Боле подробно такие колебания рассматриваются в теме «Модуляция».

Контрольные вопросы.

1. Дайте определение и приведите пример временной диаграммы дискретного сигнала.
2. Дайте определение и приведите пример временной диаграммы детерминированного сигнала.
3. Дайте определение и приведите пример временной диаграммы модулированного колебания.
4. Дайте определение и приведите пример временной диаграммы случайного сигнала.
5. u= Um SinΩt. Что такое Ω? Что такое Um? Что такое u?
6. Расшифруйте значение Ω.
7. Что называется спектром.
8. Частота первой гармоники равна 18 Гц. Определите частоту восьмой гармоники.
9. В каком случае спектр сложного сигнала непрерывный?
10. Что называется гармоникой?

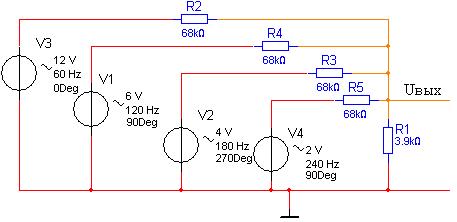
а)

б)

Рис. 11. Пример воздействия нескольких синусоидальных сигналов на линейную систему.

а) Электрическая схема линейной системы. б) Временные диаграммы сигналов.

Модуляция.

Электромагнитное колебание (радиоволна) может использоваться для передачи сообщения только в том случае, если один из параметров этого колебания меняется по закону передаваемого сообщения.

Электромагнитное колебание называется несущим. Колебание соответствующее передаваемому сообщению называется модулирующим или управляющим. Модуляция – это процесс взаимодействия колебаний высокой и низкой частот в нелинейной системе. Другими словами, модуляция – это изменение одного из параметров несущего колебания по закону управляющего (модулирующего) колебания. Нелинейная система способна создавать составляющие тока новых частот отличных от взаимодействующих колебаний. Поэтому модулированное колебание представляет собой несинусоидальное колебание, в состав которого входят синусоидальные колебания не участвующие в процессе воздействия на нелинейную систему.

При амплитудной модуляции происходит изменение амплитуды несущего колебания по закону модулирующего. Рис. 12.

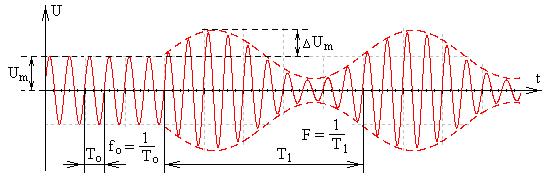
Рис. 12. Временная диаграмма амплитудно-модулированного сигнала.

Напряжение модулирующего колебания меняется по синусоидальному закону . Ток модулятора (выходного каскада передатчика) также имеет синусоидальный закон изменения 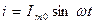. В результате воздействия модулирующего колебания на модулируемое происходит изменение амплитуды тока модулятора 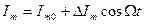. Делим на I_m и вводим понятие коэффициента модуляции. , где - коэффициент модуляции, т.е. отношение наибольшего увеличения амплитуды несущего колебания к исходному значению этой амплитуды. Коэффициент модуляции принимает значения от 0 до 1 (от 0 до 100%). При m >1 наблюдается перемодуляция несущего колебания и искажения передаваемого колебания. Диаграмма модулированного колебания при m > 1 приведена на рисунке 13.

Рис. 13. Временная диаграмма амплитудно-модулированного сигнала при m > 1.

Математические преобразования амплитудно-модулированного сигнала дают следующие результаты. Значение модулированного тока:

После преобразований, которые следует выполнить самостоятельно, получим:

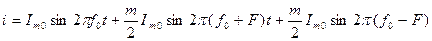, из чего следует, что

ток высокой частоты f₀ модулированный по амплитуде управляющим сигналом частотой F, представляет собой сумму трех высокочастотных токов с частотами: f_{0 ,} f₀+F и f₀ –F, где частота f₀ – несущая (основная); f₀+F – боковая верхняя; f₀ -F – боковая нижняя. Спектр такого колебания показан на рисунке 14а. В том случае, когда амплитудная модуляция осуществляется сложным гармоническим колебанием, получаем две боковые полосы частот. Рис. 14б. Для работы двух соседних по диапазону радиостанций без взаимных помех их спектры не должны пересекаться.

Задание на дом. Определить диапазон частот, занимаемый радиостанцией, работающей с амплитудной модуляцией и передающей речевой сигнал 300- 3400 Гц.

Сколько радиостанций могут работать без взаимных помех в диапазоне длинных и средних волн, если частотный диапазон сигнала составляет 200- 5000Гц.

ДВ 150-415кГц. СВ 525-1607кГц.

Рис. 14. Спектр амплитудно-модулированного сигнала.

а) в случае модуляции простым сигналом частотой F; б) при модуляции сложным сигналом, частотный диапазон которого Fн - Fв.

В случаечастотной модуляции под действием управляющего сигнала меняется частота несущего колебания (длина волны). Рис.15. Если 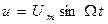, а изменение частоты пропорционально амплитуде модулирующего колебания 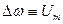, то

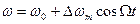. Разделив правую часть на ω₀, получим 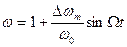. Отношение 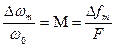называется индексом модуляции. Тогда: 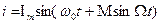. Здесь i – мгновенное значение модулированного тока; I_m – амплитуда тока; ∆ω_m – амплитуда изменения частоты несущего колебания; Ω - круговая частота модулирующего колебания; ω₀ - круговая частота несущего (модулируемого) колебания; М – индекс модуляции; t - время.

Рис. 15. Пример частотной модуляции.

Частотно- модулированный сигнал не является синусоидальным.

Максимальное отклонение частоты ∆fm от ее исходного значения f₀ называется девиациейчастоты.

Отношение девиации ∆fm к модулирующей частоте F называется индексомчастотной модуляции. Мгновенное значение тока частотно-модулированного колебания , где .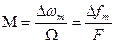

Индекс частотной модуляции прямо пропорционален амплитуде изменения управляющего сигнала и обратно пропорционален частоте Ω= 2πF.

Теоретически спектр ЧМ сигнала имеет бесконечно много пар боковых частот, но обычно пренебрегают теми составляющими, амплитуда которых меньше 0,1 амплитуды результирующего сигнала U_m.

При М>>1 число пар боковых частот равно М+1, а ширина спектра ЧМ сигнала.

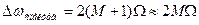
При одинаковой частоте модуляции Ω, ширина спектра ЧМ сигнала в М раз шире спектра АМ сигнала (при М>>1).

Задание на дом.Определить диапазон частот, занимаемый радиостанцией, работающей с частотной модуляцией, если передаётся музыкальная программа частотного диапазона 20 – 16000 Гц.

Сколько таких радиостанций может быть размещено в средневолновом радиовещательном диапазоне (571,4 – 186,7 м).

В качестве примера приведены технические данные промышленного радиоприёмника «Океан 209».

Диапазон ДВ 0,150-0,408 МГц 2000-735,3 м

СВ 0,525-1,605 МГц 571,4-186,9 м

КВ 3,95-5,95 МГц 75,9-50,4 м

5,95-6,20 МГц 42,3-41,0 м

9,5-9,77 МГц 81,6-30,7

11,7-12,1 МГц 25,6-24,8

УКВ 65,8-73,0 МГц 4,56-4,11 Девиация частоты 50кГц на частотах 100-200Гц. М=250-500.

Вопросы для подготовки.

1. В каких случаях электромагнитные колебания можно использовать для передачи сообщения?
2. Какое колебание называется несущим?
3. В каких системах возможна модуляция одного колебания другим?
4. Что называется модуляцией?
5. Какой параметр несущего колебания меняется при амплитудной (частотной) модуляции?
6. I_m = I_m0 (1+∆I_m/I_m0 cosωt ). Что такое Im0? Что такое ∆I_m? Что такое ω?
7. Что называется коэффициентом модуляции?
8. Свойства какого колебания характеризуется коэффициентом модуляции?
9. Свойства какого колебания характеризуется индексом модуляции?
10. Как определить коэффициент модуляции?
11. Какие составляющие имеет амплитудно-модулированное колебание, если модулирующий сигнал синусоидальный?
12. Какие составляющие имеет амплитудно-модулированное колебание, если модулирующий сигнал несинусоидальный?
13. Определить частоты боковых колебаний если ω =6,28МГц, а F=1000 Гц.
14. Чему равно наибольшее значение амплитуды тока бокового колебания?
15. Является ли модулированное колебание синусоидальным? Поясните.
16. M=∆f_m/F. Что такое М? Что такое ∆f_m? Что такое F?
17. Какова зависимость между значением индекса модуляции и амплитудой модулирующего сигнала?
18. При какой модуляции спектр модулированного сигнала шире (уже)?
19. Как зависит ширина спектра частотно-модулированного сигнала от индекса модуляции?