Вынужденные колебания в последовательном контуре.

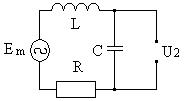
Рис. 19. Электрическая схема последовательного колебательного контура.

Обычно рассматривается установившийся режим, когда собственные колебания, если они возникли, успели полностью затухнуть.

ЭДС генератора (Рис. 19) 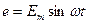, где Е – амплитуда колебаний генератора; ω – частота напряжения генератора. Внутреннее сопротивление генератора, работающего на последовательный контур мало и им можно пренебречь. Полное сопротивление контура на любой частоте: ; , .

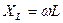Знак минус указывает, что емкостное сопротивление обратно пропорциональное частоте, создает отставание фазы напряжения на емкости, по отношению тока. Модуль полного сопротивления контура .

Зависимость реактивных сопротивлений от частоты выражаются графиком представленным на Рис. 20. Реактивные сопротивления являются комплексными величинами.

Из графика видно, что существует такое значение частоты ω_0, при котором реактивные сопротивления равны X _L= X_C. В этом случае общее реактивное сопротивление равно нулю, а ток в контуре достигает наибольшего значения и определяется активным сопротивлением контура. Абсолютная величина амплитуды тока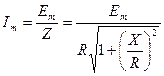

Рис. 20. Зависимости реактивных сопротивлений элементов колебательного контура.

Напряжения на реактивных сопротивлениях взаимно компенсируют друг друга, равны между собой по модулю и достигают наибольшего значения. По этим причинам резонанс в последовательном контуре называется резонансом напряжений.

График зависимости тока (амплитуды или действующего значения) в контуре от частоты генератора называют кривой резонанса. Рис.21.

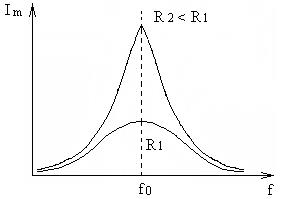
Рис. 21. Резонансные кривые контуров имеющих различные сопротивления потерь.

Резонансная частота зависит только от индуктивности и емкости, а амплитуда тока при резонансе – от активного сопротивления. Различные колебательные контуры имеют различную форму резонансной кривой и значение амплитуды тока. Поэтому при сравнении свойств различных контуров пользуются не абсолютным значением тока, а относительным 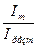, а по оси частот откладывается не абсолютное значение частоты, а отношение 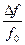_. Эти характеристики называют амплитудно-частотными.

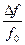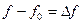Для сравнения свойств различных контуров часто используют амплитудно-частотную характеристику, построенную в относительных координатах, т.е. как зависимость относительного изменения тока в контуре от относительной расстройки , или абсолютной расстройки _∆f. Рис. 22. Разность частот (или ) называют абсолютной расстройкой. Отношение - называют относительной расстройкой. Величина 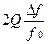называется обобщенной расстройкой.

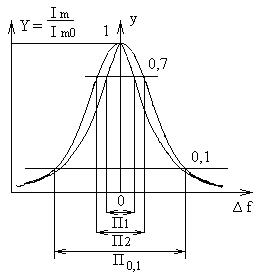
Рис. 22. Амплитудно-частотные характеристики двух контуров.

Способность колебательного контура пропускать колебания одних частот и задерживать колебания других, отличных от резонансной частоты характеризуется полосой пропускания, которая обозначается символом П или _∆f_пр.

Какой бы добротностью ни обладал колебательный контур, и какую бы собственную частоту ни имел, его характеристика не является прямоугольной. Коэффициент непрямоугольности определяется как отношение полос пропускания на уровнях 0,707 и 0,1. Для любого контура он равен 10 (Рис. 22). В реальных условиях внутреннее сопротивление генератора не равно нулю и оно добавляется к активному сопротивлению контура. Следовательно, при работе на последовательный колебательный контур, внутреннее сопротивление генератора должно быть возможно меньше.

Примером практического применения резонанса напряжения является настройка входного контура LCR радиоприемника на частоту принимаемого радиосигнала (Рис. 23).

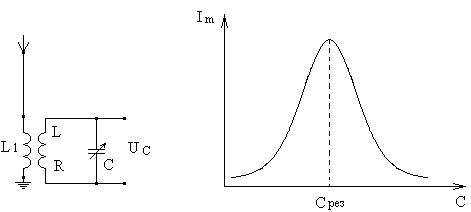
Рис. 23. Схема входной цепи радиоприёмника и зависимость амплитуды тока от ёмкости конденсатора.

Полоса пропускания контура – это разность частот, в пределах которой коэффициент передачи (амплитуда тока) не снижается более определенной величины. Обычно полосу пропускания определяют на уровне 0,7 от значения коэффициента передачи на резонансной частоте. Теоретически полоса пропускания контура определяется следующим образом: 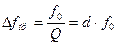. Чем выше значение добротности, тем уже полоса пропускания.

Отношение амплитуды напряжения на одном из реактивных элементов контура к амплитуде напряжения генератора называется коэффициентом передачи 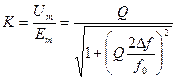. Это уравнение является уравнением амплитудно-частотной характеристики контура.

1. Какой колебательный контур называется параллельным; последовательным?
2. Что такое переходный процесс, в каком случае он возникает?
3. Чему равно полное сопротивление последовательного контура?
4. Что называется резонансом ,и при каких условиях возникает резонанс?
5. Почему резонанс в последовательном контуре называется резонансом напряжений?
6. Как меняется форма резонансной кривой при уменьшении активного сопротивления контура?
7. Что называется расстройкой контура? Какие виды расстройки вам известны.
8. Как определить полосу пропускания контура?
9. От каких величин зависит полоса пропускания контура?
10. Приведите пример практического применения параллельного (последовательного) контура.