Теорема о переносе вектора силы вдоль линии действия
Основные понятия и аксиомы
Статика - наука о равновесии механической системы. В статике рассматриваются три основные задачи:
1) сложение и приведение системы сил, т.е. замене данной системы сил другой, более простой, оказывающей то же воздействие на механическую систему, что и исходная система сил;
2) определение необходимых и достаточных условий равновесия механической системы по отношению к определенной системе координат;
3) определение центра тяжести механической системы.
Законы статики имеют большое значение в инженерных расчетах.
1.1. Определения
Материальной точкой называют тело, при изучении движения которого можно пренебречь его размерами и его вращением. Возможность такого пренебрежения зависит от конкретных условий той или иной задачи. Например, автобус можно считать материальной точкой при изучении его движения по дороге, а футбольный мяч, летящий по полю, нельзя считать материальной точкой, поскольку при движении он вращается.
Механической системой, или просто системой, называется выделенная каким-либо образом совокупность материальных точек.
Абсолютно твердым телом (или неизменяемой механической системой) называют механическую систему, расстояние между точками которой не изменяется. В дальнейшем абсолютно твердое тело будем называть просто твердым телом.
Реальные тела обычно могут изменять свою форму, при этом изменяются и расстояния между отдельными точками тел. Однако в ряде случаев эти изменения (деформации) настолько малы, что ими можно пренебречь. Поэтому абсолютно твердое тело является моделью материального тела.
Силой называют одну из векторных мер действия одного материального объекта на другой рассматриваемый объект. Сила характеризуется величиной (модулем), направлением и точкой приложения. Такие объекты называют векторами. Следуя Рене Декарту (1596-1650), вектора задают проекциями на оси координат. Силу как величину векторную обозначают какой-либо буквой со знаком вектора, например, 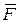 или
или 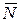 . Для выражения числового значения силы (модуля силы) используется знак модуля от вектора, т.е.
. Для выражения числового значения силы (модуля силы) используется знак модуля от вектора, т.е. 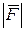 ,
, 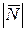 или F, N.
или F, N.
Имеются две меры действия: скалярная (численная) и векторная. За эталон численного значения силы принимают значение линейной силы упругости, например, пружинного динамометра, которая пропорциональна его удлинению. Сила измеряется в ньютонах (Н).
Системой сил называют совокупность сил, действующих на рассматриваемый объект.
Системой сил, эквивалентной нулю, (равновесной системой сил) называют такую систему сил, действие которой на объект не приводит к изменению состояния покоя или движения по инерции этого объекта.
Равнодействующей силой рассматриваемой системы сил называют силу, действие которой на объект эквивалентно действию этой системы сил.
Равновесная система сил имеет равнодействующую, равную нулю.
Уравновешивающей силой заданной системы сил считается такая сила, добавление которой к заданной дает новую систему, эквивалентную нулю.
| Линия, вдоль которой действует сила, называется линией действия этой силы (рис.1.1). |
| Рис.1.1 |
|
| Рис.1.2 |
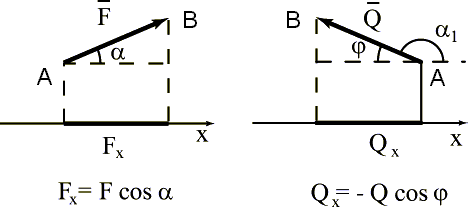
Проекция силы на ось. Изобразим силу 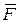 вектором
вектором 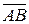 (рис.1.2). Опустим перпендикуляры из начала А и конца В вектора на данную ось x, получим отрезок
(рис.1.2). Опустим перпендикуляры из начала А и конца В вектора на данную ось x, получим отрезок 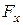 , называемый проекцией силы
, называемый проекцией силы 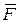 на ось x. Проекция силы на ось является скалярной величиной, потому что не имеет собственного направления, а определяется направлением оси. Проекция силы будет положительна, если направление вектора силы составляет с положительным направлением оси острый угол-
на ось x. Проекция силы на ось является скалярной величиной, потому что не имеет собственного направления, а определяется направлением оси. Проекция силы будет положительна, если направление вектора силы составляет с положительным направлением оси острый угол- 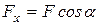 , и отрицательна, если угол тупой:
, и отрицательна, если угол тупой: 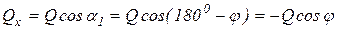 .
.
Если дана сила 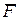 , расположенная в пространстве, то ее координаты на прямоугольные оси x, y, z (рис.1.3) вычисляются по формулам:
, расположенная в пространстве, то ее координаты на прямоугольные оси x, y, z (рис.1.3) вычисляются по формулам:
Fx = 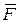 ×
× 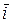 = F sinq cosj , Fy =
= F sinq cosj , Fy = 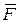 ×
× 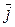 = F sinq sinj , Fz =
= F sinq sinj , Fz = 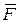 ×
× 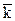 = F cosq . (1.1)
= F cosq . (1.1)
Здесь 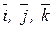 - единичные векторы, направленные по осям координат x, y, z; Fx, Fy , Fz - скалярные величины, которые являются проекциями силы F на оси координат. Иногда по проекциям силы определяют модуль силы и косинусы углов ее с осями координат по формулам: - единичные векторы, направленные по осям координат x, y, z; Fx, Fy , Fz - скалярные величины, которые являются проекциями силы F на оси координат. Иногда по проекциям силы определяют модуль силы и косинусы углов ее с осями координат по формулам:
| 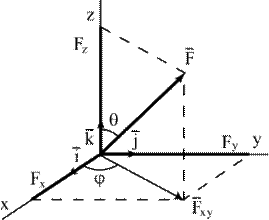 Рис.1.3
Рис.1.3
|
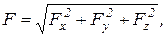 (1.2)
(1.2)
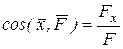 ,
, 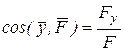 ,
, 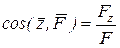 .
.
Аксиомы статики
Аксиома 1. Если на свободное абсолютно твердое тело действует две силы, то тело может находиться в состоянии равновесия тогда и только тогда, когда эти силы равны по модулю (F1= F2) и направлены вдоль одной общей линии действия в противоположные стороны (рис.1.4).

| Эта аксиома определяет один из главных принципов теоретической механики. Силы  и и  находятся в равновесии, т.е. образуют систему сил, эквивалентную нулю, находятся в равновесии, т.е. образуют систему сил, эквивалентную нулю,
|
| Рис.1.4 |
или равновесную систему сил.
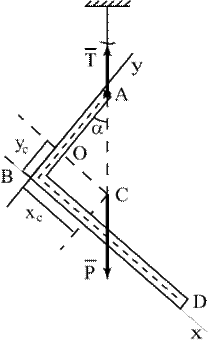
| лены между собой. Центр тяжести полученного изогнутого под углом 900 стержня расположен в точке С (рис.1.5) с координатами 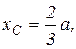 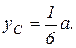 Конец А подвешен на нити. Определить угол a в положении равновесия.
Решение. На рассматриваемый изогнутый под углом 900 стержень действует две силы: натяжение нити Конец А подвешен на нити. Определить угол a в положении равновесия.
Решение. На рассматриваемый изогнутый под углом 900 стержень действует две силы: натяжение нити 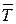 и вес и вес 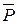 . .
|
| Рис.1.5 |
Пример. Два однородных стержня АВ и ВD (AB= а, BD=2a) жестко скреп- Если стержень находится в равновесии, то 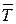 и
и 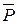 должны лежать вдоль одной линии действия, это и определяет угол
должны лежать вдоль одной линии действия, это и определяет угол 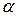 , следовательно, задача сводится к геометрической.
, следовательно, задача сводится к геометрической.
Рассмотрим прямоугольный треугольник АОС
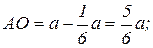
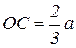 .
.
Тогда 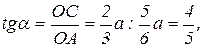
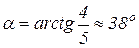 .
.
Аксиома 2. Действие заданной системы сил на абсолютно твердое тело не изменяется, если к ней прибавить или от нее отнять равновесную систему сил (систему сил, эквивалентную нулю).
Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные в одной точке и направленные под углом друг к другу эквивалентны одной силе (равнодействующей) приложенной в той же точке и равной по модулю и направлению диагонали параллелограмма, стороны которого изображают величины и направления обеих заданных сил (рис.1.6а).
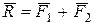 . (1.3)
. (1.3)
Модуль равнодействующей 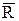 равен длине диагонали параллелограмма, стороны которого образованы слагаемыми векторами (правило параллелограмма). Модуль равнодействующей можно вычислить, используя теорему косинусов:
равен длине диагонали параллелограмма, стороны которого образованы слагаемыми векторами (правило параллелограмма). Модуль равнодействующей можно вычислить, используя теорему косинусов:
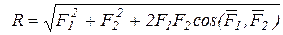 .
.
Опытная проверка правила сложения сил проводится следующим образом. Тело подвергается совместному действию нескольких, равно растянутых нитей. Далее на опыте исследуется, как располагаются все нити, и измеряются значения сил натяжения нитей (по показаниям динамометров) при равновесии (рис.1.6б). При этом можно убедиться, что нити расположены в соответствии с аксиомой параллелограмма сил.
| а | 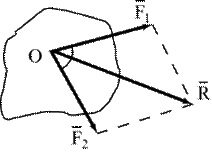
| б | 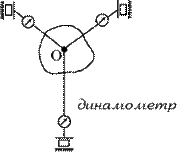
|
| Рис.1.6 |
Аксиома 4. При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие.
Определения
Связью для твердого тела или материальной точки называют материальные объекты (тела, точки), которые не дают перемещаться в обе стороны, т.е. ограничивают свободу перемещения рассматриваемого твердого тела или материальной точки.
Силы, действующие со стороны связей, называют реакциями связей.
Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу.
В плоскости твердое тело имеет три независимых перемещения: перемещения в двух ортогональных направлениях и вращение вокруг оси, перпендикулярной этой плоскости. Максимальное число независимых перемещений тела определяет число его степеней свободы. Следовательно, в плоскости тело имеет три степени свободы. В пространстве твердое тело имеет шесть независимых перемещений (перемещения в трех ортогональных направлениях и вращение в каждой из плоскостей), т.е. имеет шесть степеней свободы.
Любая связь ограничивает ту или иную степень свободы. Если в плоскости на тело наложить определенным образом три связи, то оно будет неподвижно. В пространстве на тело нужно наложить определенным образом шесть связей, чтобы оно находилось в состоянии покоя.
Аксиома 5 (аксиома связи). Всякую связь можно отбросить и заменить ее реакцией - силой (в простейшем случае) или системой сил (в общем случае).
Очень важно научиться правильно заменять отброшенную связь реакциями связей. Это одна из главных задач при изучении статики.
Комментарии к аксиоме связей
Рассмотрим, как направлены реакции некоторых основных видов связей.
Гладкая поверхность (плоскость) или опора. Такая поверхность не дает телу перемещаться только в направлении общей нормали к поверхностям соприкасающихся тел в точке их касания (рис.1.7а). Поэтому проекция реакции на направление, касательное к поверхности, равна нулю, а значит реакция гладкой поверхности, плоскости или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке. Когда одна из соприкасающихся поверхностей является точкой (рис.1.7б), то реакция направлена по нормали к другой поверхности.
| а | 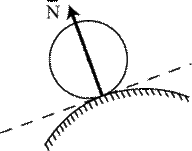
| б | 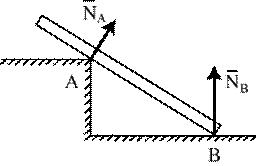
|
| Рис.1.7 |
Шарнирные опоры. Плоским шарниром или шарниром (2 связи, 1 степень свободы) называют устройство, позволяющее твердому телу поворачиваться в плоскости вокруг оси, перпендикулярной этой плоскости. Например, если два тела соединены осью, проходящей через отверстия в этих телах, то такое соединение будет шарнирным, или просто шарниром. Осевая линия будет осью шарнира. Шарнир накладывает
В пространстве шарниры бывают цилиндрические (5 связей, одна степень свободы), шаровые (3 связи, 3 степени свободы) и карданный вал (4 связи, 2 степени свободы).
Гибкие связи. Невесомый стержень шарнирно закрепленный по концам. Связь, осуществленная в виде гибкой нерастяжимой нити (троса, каната и т.д.), или невесомого стержня, шарнирно закрепленного по концам, не дает телу удаляться от точек подвеса вдоль нити или стержня. Поэтому реакции натянутых нитей или стержней TA и TB направлены вдоль нитей или вдоль стержня к точке их подвеса (рис.1.8).

|
| Рис.1.8 |
Балки, как правило, опираются на каменные стены, железобетонные конструкции и т.д. Для этого используют специальные опорные части. Чаще всего в инженерной практике применяют следующие типы опор: шарнирно -подвижные и шарнирно - неподвижные.
Шарнирно- подвижная опора (рис.1.9а) допускает перемещение балки (тела) в направлении, параллельном опорной плоскости и поворот балки относительно опоры на угол j. Перемещение, перпендикулярное опорной плоскости, отсутствует. В соответствии с этим в шарнирно-подвижной опоре возникает реакция, проекция на одно из направлений известна – равна нулю, остается одна неизвестная_ проекция на нормаль к направлению возможного движения, т.е. перпендикулярная опорной поверхности, которую будем обозначать V. Закрепление балки (тела) с помощью такой опоры накладывает на нее одну связь, т.е.
| а | 
| б | 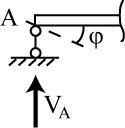
| в | 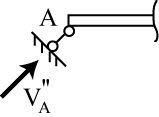
|
| Рис.1.9 |
балка лишается одной степени свободы.
В строительной документации такую опору принято изображать в виде короткого стержня (рис.1.9в) с шарнирами на концах (опорная связь).
Шарнирно - неподвижная опора (рис.1.10а) допускает поворот балки (тела) относительно опоры и не допускает линейных перемещений. Шарнирно-неподвижная опора лишает балку двух степеней свободы. Опорная реакция 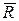 проходит через ось шарнира под углом a (рис.1.10б). Реакция этой опоры содержит две неизвестные – модуль реакции R и ее направление, т.е. угол a. На практике часто, но не всегда принято раскладывать
проходит через ось шарнира под углом a (рис.1.10б). Реакция этой опоры содержит две неизвестные – модуль реакции R и ее направление, т.е. угол a. На практике часто, но не всегда принято раскладывать 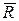 на два ортогональных направления, например, на горизонтальное HA и вертикальное VA, что и символизируется двумя опорными стержнями - носителями этих двух составляющих, пересекающихся в точке А (рис.1.10в). Тогда
на два ортогональных направления, например, на горизонтальное HA и вертикальное VA, что и символизируется двумя опорными стержнями - носителями этих двух составляющих, пересекающихся в точке А (рис.1.10в). Тогда
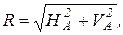
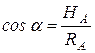 .
.
| а | 
| б | 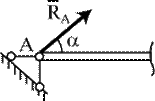
| в | 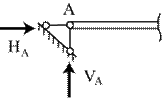
|
| Рис.1.10 |
Итак, если на балку действует нагрузка, расположенная в одной плоскости, то для неподвижного состояния балки с ее основанием необходимо наложить
| а б | 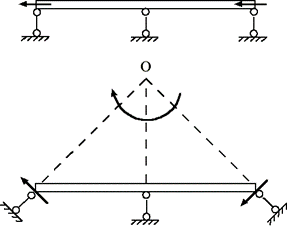 Рис.1.11
Рис.1.11
|
на нее три связи.
Это условие является необходимым, но не достаточным. Например, в случае, когда балка соединена с основанием при помощи трех опорных стержней, параллельных друг другу (рис.1.11а). Балка под действием нагрузки будет перемещаться в направлении, параллельном опорной плоскости, т. е. в горизонтальном (теорема о поступательном движении тела).
Также недопустимо для конструкций, которые должны быть неподвижными при любых нагрузках, соединение с основанием при помощи трех стержней, направления которых пересекаются в одной точке (здесь это точка О), т.к. возможен мгновенный поворот балки в плоскости вокруг точки О (теорема о поступательном движении тела) (рис.1.11б).
Таким образом, недопустимо соединение балки (тела) с основанием при помощи трех шарнирно-подвижных опор, направления которых были бы параллельны друг другу или пересекались в одной точке.
| а б в | 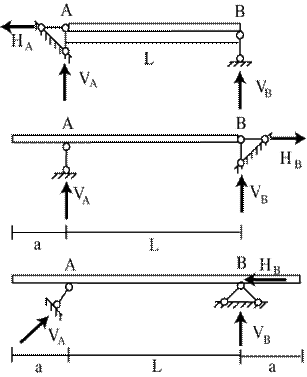 Рис.1.12
Рис.1.12
| В инженерной практике чаще всего балки соединяются с основанием при помощи указанных выше опор или их сочетаний. Наиболее широко распространены следующие типы балок: однопролетная балка (рис.1.12а), имеющая по концам шарнирные опоры; расстояние между опорами L называется пролетом балки; консольная (рис.1.12б, в) балка, имеющая один или два свободных конца. |
В опорах балок, изображенных на рис.1.12а-в, от заданной плоской системы сил возникает три реакции опор.
Деформации элементов конструкций обычно малы, и ими пренебрегают при составлении уравнений равновесия. Это выражают аксиомой отвердевания.
Аксиома 6 (принцип отвердевания). Если деформируемое тело находится под действием некоторой системы сил в равновесии, то равновесие не нарушится, если это тело отвердеет, т.е. станет абсолютно твердым.
С помощью этой аксиомы устанавливается, в частности, связь между условиями равновесия сил, приложенных к твердому и деформируемому телам. Из принципа следует, что условия равновесия, являющиеся необходимыми и достаточными для абсолютно твердого тела, являются необходимыми, но не достаточными для деформируемого тела. Достаточные условия равновесия деформируемых тел устанавливаются в курсах сопротивления материалов и теории упругости.
Теорема о переносе вектора силы вдоль линии действия
Теорема. Действие силы на твердое тело не изменится от переноса вектора силы вдоль своей линии действия.
Пусть в точке А твердого тела приложена сила 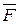 (рис.1.13а). К этой силе добавим систему сил, эквивалентную нулю, на ее линии действия, причем (рис.1.13а). К этой силе добавим систему сил, эквивалентную нулю, на ее линии действия, причем 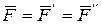 (рис.1.13б). Тогда система сил (рис.1.13б). Тогда система сил 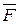 и и 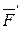 , согласно аксиоме 1, эквивалентна нулю, и, согласно аксиоме 2, ее можно отбросить. Останется одна сила , согласно аксиоме 1, эквивалентна нулю, и, согласно аксиоме 2, ее можно отбросить. Останется одна сила 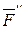 , равная заданной силе , равная заданной силе 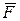 , приложенная в точке В (рис.1.13в). Сила , приложенная в точке В (рис.1.13в). Сила 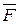 приложена в точка А. Она эквивалентна такой же по модулю и направлению силе приложена в точка А. Она эквивалентна такой же по модулю и направлению силе 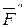 , приложенной в точке В, где точка В - любая точка линии действия силы , приложенной в точке В, где точка В - любая точка линии действия силы 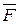 . .
| а б в | 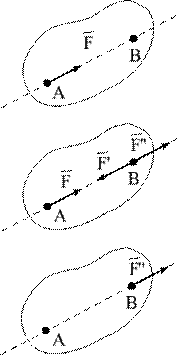 Рис.1.13
Рис.1.13
|
Векторные величины, которые можно прикладывать в любой точке линии действия, называют скользящими. Сила, приложенная к абсолютно твердому телу, есть вектор скользящий. Таким образом, аксиома 1 равносильна допущению о том, что силы, действующие на твердые тела – скользящие.
| <== предыдущая лекция | | | следующая лекция ==> |
| Основы охраны труда. Правовые основы законодательства. | | | Основные виды законодательства, установленного государством в отношении предприятий. Антимонопольное законодательство. |
Дата добавления: 2019-12-09; просмотров: 711;










