Движение частиц в прямоугольной потенциальной яме
& Литература: [1], [2], [7], [8].
 Проанализируем движение частицы в прямоугольной потенциальной яме, изображенной на рисунке 19.1.
Проанализируем движение частицы в прямоугольной потенциальной яме, изображенной на рисунке 19.1.
В каждой из областей I, II, III (рис.19.1) реализуется свободное движение. Так что можно использовать формулы (18.6) и (18.7).
В области I, где U = ¥, для обеспечения конечности Y-функции следует положить A = 0.
Тогда Y1 = B exp (¥ x) = 0. (19.1)
В области II
Y2 = A2 exp (i k2 x) + B2 exp (–i k2 x), (19.2)
где k2 = 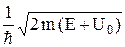 . (19.3)
. (19.3)
В области III Y3 = A3 exp(–g x), (19.4)
где g = 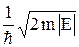 . (19.5)
. (19.5)
Из полученных решений для отдельных областей нужно «сшить» единую Y-функцию, удовлетворяющую стандартным условиям и имеющую непрерывную производную везде, кроме точки x = 0.
Условие сшивания в точке x = 0 дает A2 = – B2 .
Условия сшивания в точке x = a с учетом последнего равенства принимают вид: A2 2 i sin (k2 a) = A3 exp (–g a), (19.6)
A2 2 i cos (k2 a) = – 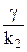 A3 exp (–g a). (19.7)
A3 exp (–g a). (19.7)
При отличных от нуля A2 и A3 соотношения (19.6) и (19.7) эквивалентны равенству tg (k2 a) = – k2 / g. (19.8)
Оно имеет место лишь при определенных значениях E. Именно эти значения и составляют энергетический спектр.
Уравнение (19.8) можно решить, например, графическим методом или численно на компьютере. Анализ решения приводит к следующим заключениям:
§ минимально возможное значение энергии (энергия основного состояния) E0 > – U0 в полном соответствии с соотношением неопределенностей Гейзенберга;
§ число возможных значений энергии конечно и растет с ростом параметра U0 a2;
§ при условии 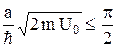 решений не существует, то есть в случае достаточно узкой и мелкой ямы финитное движение невозможно.
решений не существует, то есть в случае достаточно узкой и мелкой ямы финитное движение невозможно.
Для бесконечно глубокой потенциальной ямы (U0 ® – ¥) соотношение (19.8) дает: E + U0 » En = 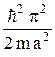 (n + 1)2 , (19.9)
(n + 1)2 , (19.9)
где n –– квантовое число (n = 0, 1, 2,…).
Волновая функция в этом случае при 0 £ a £x имеет вид:
Y = 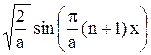 . (19.10)
. (19.10)
Вне указанной области она равна нулю.
Движение микрочастицы в потенциальной яме качественно отличается от движения классической частицы:
§ энергетический спектр микрочастицы дискретен;
§ уровень минимально возможной энергии выше дна потенциальной ямы;
§ микрочастицу можно обнаружить вне ямы вблизи ее края, если яма здесь имеет конечную глубину;
§ внутри ямы есть точки (узлы волновой функции), недоступные для микрочастицы.
При n ® ¥ различия в поведении микрочастиц и классических частиц исчезают. В этом проявляется принцип соответствия.
? Контрольные вопросы
1. Какие конкретные системы моделирует задача о прямоугольной потенциальной яме?
2. Какие значения принимает потенциальная функция в различных областях ямы, и какой вид для них имеет волновая функция?
3. Какие свойства волновой функции используются при нахождении энергетического спектра микрочастицы в прямоугольной потенциальной яме?
4. Расскажите об энергетическом спектре микрочастицы в прямоугольной потенциальной яме. Почему энергетический спектр электронов в металле называют квазинепрерывным, и почему его дискретность оказывается существенной?
5. Сравните поведение микрообъекта и классической частицы в потенциальной яме.
|
19.1.Для потенциальной ямы, изображенной на рисунке 19.2, нарисуйте графики волновых функций микрочастиц, обладающих энергиями E1 и E2.
19.2.  Решите уравнение Шредингера для микрочастицы, находящейся в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками и найдите энергетический спектр.
Решите уравнение Шредингера для микрочастицы, находящейся в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками и найдите энергетический спектр.
| 0, если 0 £ x £ a, 0 £ y £ b, 0 £ z £ c. ¥, если x < 0, x > a, y < 0, y > b, z <0, z > c. |
19.3.  Найдите волновую функцию и энергетический спектр частицы, находящейся в потенциальном поле, определяемом следующим образом:
Найдите волновую функцию и энергетический спектр частицы, находящейся в потенциальном поле, определяемом следующим образом:
19.4.
 |
На рисунках 19.3 и 19.4 изображены графики действительной части волновой функции электрона в одномерной прямоугольной потенциальной, показанной на рис. 19.1. Чем принципиально отличаются состояния с указанными Y-функциями? Что можно сказать об энергии этих состояний? Почему различаются расстояние между узлам (рис. 19.4) в яме и вне ямы? Что означает различие амплитуды колебаний Y-функции (рис. 19.4) в яме и вне ямы?
§20. Прохождение частицы через потенциальный барьер.
Туннельный эффект
& Литература: [1], [2], [7], [8].
Прохождением через потенциальный барьер называют движение частицы в области пространства, где потенциальная функция имеет максимум. В качестве примеров подобных движений можно назвать: перекатывание шарика через горку, вырывание электрона из металла электрическим полем (холодная эмиссия), вылет a-частицы из тяжелого ядра (a-распад) и другие.
Укажем основные идеи и этапы решения задачи о прямоугольном потенциальном барьере, изображенном на рисунке 20.1.
Барьер имеет ширину a и высоту U0. Энергия частицы – E.
Для каждой из указанных на рисунке областей I, II, и III решение уравнения Шредингера имеет вид волновой функции свободного движения:
Yj = Aj exp (i kj x) + Bj exp–i kj x), (20.1)
где j = 1, 2, 3; k1 = k3 = 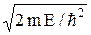 , (20.2)
, (20.2)
k2 = 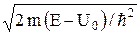 . (20.3)
. (20.3)
Цель расчетов – найти коэффициент отражения барьера
R = |B1|2 / |A1|2, (20.4)
а также коэффициент прозрачности D = 1 – R. (20.5)
 Эти коэффициенты представляют собой вероятности того, что частица, соответственно, отразится от барьера или что она преодолеет его.
Эти коэффициенты представляют собой вероятности того, что частица, соответственно, отразится от барьера или что она преодолеет его.
Произвольные постоянные Aj и Bj должны обеспечивать для волновой функции выполнение стандартных условий, а также непрерывность производной. Соответствующие условия на границах x = 0 и x = a называют условиями сшивания.
Положим для определенности, что частицы попадают на барьер только слева (рис.20.1). Тогда B3 = 0. Условия сшивания в точке x = 0 принимают вид:
A1 + B1 = A2 + B2, (20.6)
k1 A1 – k1B1 =k2 A2 – k2B2 , (20.7)
а в точке x = a:
A2 exp (i k2 a) + B2 exp (–i k2 a) = A3 exp (i k1 a) , (20.8)
k2 A2 exp (i k2 a) – k2 B2 exp (–i k2 a) =k1 A3 exp (i k1 a) . (20.9)
Исключая из системы (20.8) и (20.9) вначале A2, а затем B2, получим
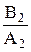 =
= 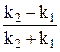 exp (2 i k2 a). (20.10)
exp (2 i k2 a). (20.10)
Проделав аналогичные процедуры с (20.6) и (20.7), найдем
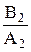 =
= 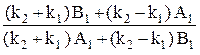 . (20.11)
. (20.11)
Приравнивая (20.10) и (20.11), вычислим отношение
R = 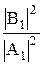 =
= 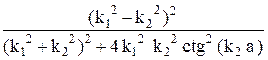 . (20.12)
. (20.12)
Заметим, что формула (20.12) справедлива как для случая E < U0 (высокий барьер), так и для случая E > U0 (низкий барьер).
Из (20.12) следует, что
D = 1 – R = 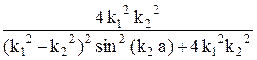 . (20.13)
. (20.13)
На практике пользуются приближенной формулой для коэффициента прозрачности, которая получается из (20.13), если положить k1 = k, k2 = i k,
a k >> 1: D ≈ exp (– 2 a k) = exp 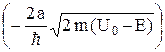 . (20.14)
. (20.14)
 В отличие от классической частицы микрообъект может преодолеть даже высокий (E < U0) потенциальный барьер с вероятностью, определяемой формулой (20.13) (или (20.14)). Энергия E при этом остается постоянной, то есть работа над частицей не совершается. Преодоление микрочастицей высокого потенциального барьера без совершения работы называют туннельным эффектом.
В отличие от классической частицы микрообъект может преодолеть даже высокий (E < U0) потенциальный барьер с вероятностью, определяемой формулой (20.13) (или (20.14)). Энергия E при этом остается постоянной, то есть работа над частицей не совершается. Преодоление микрочастицей высокого потенциального барьера без совершения работы называют туннельным эффектом.
Преодоление потенциального барьера произвольной формы можно рассматривать как последовательное прохождение множества узких почти прямоугольных барьеров шириной dx и высотой U(x) – E (рис. 20.2). Перемножив вероятности прохождения этих барьеров, найденные по формуле (20.14), получим выражение для искомого коэффициента прозрачности:
D ≈ exp 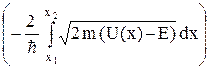 . (20.15)
. (20.15)
Пределы интегрирования x1 и x2 (рис.20.2) являются корнями уравнения
U(x) – E = 0.
? Контрольные вопросы
1. Расскажите о потенциальных барьерах для классических частиц и для микрообъектов. Какие величины характеризуют преодоление барьеров?
2. Расскажите о туннельном эффекте.
3. Какой вид имеет волновая функция в различных областях прямоугольного потенциального барьера?
4. Какие условия сшивания используются при решении задачи о прямоугольном потенциальном барьере?
5. Сравните преодоление потенциального барьера классической частицей и микрообъектом.
6. Как подсчитать коэффициент прозрачности для барьера произвольной формы?
7. Приведите примеры проявления туннельного эффекта? Имеет ли он место для макроскопических тел?
|
21.3Получите выражения (20.12) и (20.13) для коэффициента отражения и для коэффициента прозрачности прямоугольного потенциального барьера.
21.4Получите из (12.13) приближенную формулу (12.14).
21.5Электрон проходит через потенциальный барьер, создаваемый полем E. Максимальное значение потенциальной энергии превышает энергию электрона на величину U0. Определите коэффициент прозрачности барьера D. D = exp 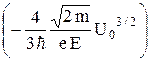 .
.
Дата добавления: 2021-11-16; просмотров: 620;











