Основы теории теней. Тени точки, отрезка прямой линии, плоской фигуры.

Этапы построения теней. Факельное и солнечное освещение. Тени собственная и падающая. Лучевая плоскость. Обертывающая лучевая поверхность. Граница (контур) собственной и падающей теней. Действительные и мнимые тени. Свойства теней. Правила построения теней. Падающая тень точки. Зависимость тени от положения точки в пространстве. Построение теней (падающих на горизонтальную и фронтальную плоскости проекций, ось Х). построение теней, падающих на плоскости общего положения. Последовательность построения тени отрезка линии. Построение тени отрезка линии.

Для придания двумерному изображению наглядности, большей выразительности прибегают к построению собственных и падающих теней. Особенно широко используются тени при оформлении архитектурных проектов.

Построение теней включает два этапа:
– построение границ теней (геометрию теней);
– графические приемы выявления светотени (отмывка, тушевка и т. п.).

На лекциях по архитектурной графике рассматривается геометрия теней, на практических занятиях – графические приемы, наиболее часто используемые в практике ландшафтного проектирования.

При построении теней обычно предполагают, что свет распространяется прямолинейно. Освещение называют факельным, если источник света удален от объекта на незначительное расстояние. Лучи света при этом образуют связку прямых, центром которых служит источник света (фонарь, прожектор и т. п.) Если же источник света бесконечно удален, то освещение называют параллельным или солнечным, т. к. центр связки световых лучей (солнце или луна) находится в «бесконечности», и лучи идут практически параллельно друг другу. Второй случай наиболее распространен.

Тенью в архитектурной графикеназывают часть пространства, через которую не проходят световые лучи. Область тени находится между собственной и падающей тенями предмета.

Собственной тенью называют неосвещенные участки объекта.

Падающей тенью называют тень объекта на плоскости проекций, на другом объекте или тень от одной части объекта на другой его части.

Лучевая плоскость – это множество световых лучей, проходящих через некоторую прямую. Множество световых лучей, касающихся данного тела (обертывающих его), называется обертывающей лучевой поверхностью. При параллельном освещении эта поверхность – цилиндрическая, при центральном – коническая (рис. 41). Линия касания обертывающей лучевой поверхности с данным телом называется границей или контуром собственной тени. Линия пересечения лучевой поверхности с плоскостью или другой поверхностью образует границу или контур падающей тени.

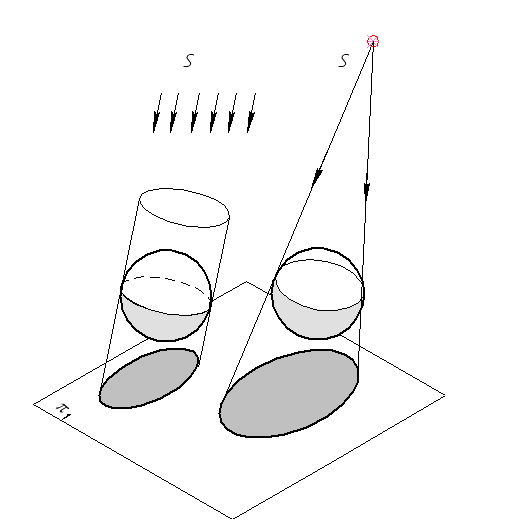
Рис. 41. Обертывающие лучевые поверхности – цилиндрическая
и коническая
Тени, расположенные на передней полуплоскости p₁ и верхней полуплоскости p₂, называют действительными; тени, расположенные за фронтальной плоскостью p₂ – воображаемыми, или мнимыми.

Для построения теней необходимо наличие двух проекций предмета, полностью определяющих его форму.

Тени при параллельном освещении моделируют параллельные проекции. Свойства этих проекций порождают следующие свойства теней:

тень точки на плоскость есть точка пересечения светового луча, проходящего через эту точку, с плоскостью;
тень от прямой на плоскость или поверхность представляет собой линию пересечения лучевой плоскости, образованной лучами света, проходящими через прямую, с плоскостью или поверхностью;
тень прямой параллельна самой прямой и равна ей по величине, если прямая параллельна плоскости, на которую падает тень;
тень прямой совпадает по направлению с проекцией светового луча, если прямая перпендикулярна к плоскости проекций;
при одностороннем освещении плоской фигуры одна из ее сторон окажется освещенной, а другая будет находиться в собственной тени.

Рассмотрим некоторые правила построения теней при солнечном освещении на примерах теней точки, прямой и плоской фигуры.

В архитектурном проектировании принято постоянное параллельное (стандартное) направление освещения. На рис. 42 представлено наглядное изображение и эпюр образования направления стандартного освещения – S(S^/,S^//). pЭто направление представляет собой диагональ куба, которая наклонена к плоскости ₁ под углом 35° 16' 16", а в проекциях на p₁ и p₂ угол наклона к оси X равен 45°.

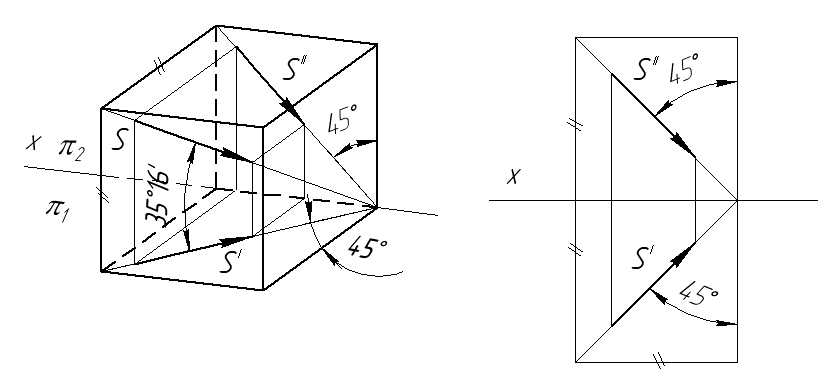
Рис. 42. Наглядное изображение и эпюр образования стандартного освещения
В дальнейшем, если не указаны другие условия, построение теней будут выполняться для параллельного стандартного освещения.

2. Падающей тенью точки является точка пересечения луча, проходящего через нее, с поверхностью, на которую падает тень. Так тень от точки на плоскость есть точка пересечения светового луча, проходящего через нее, с этой плоскостью. Фактически тенью точки является след прямой, проведенной через точку параллельно направлению освещения. Можно рассмотреть три различных положения точки и соответственно возможных варианта построения падающей тени точки:

– тень от точки падает на горизонтальную плоскость проекций p₁ (рис. 43);

– тень от точки падает на ось ^ Х (рис. 44);

– тень от точки падает на фронтальную плоскость проекций p₂ (рис. 45).

Рассмотрим последовательность построения теней точек при их различном положении в пространстве. На рис. 43, 44, 45 приведены наглядные изображения и ортогональные проекции построений теней точек А, В и С.

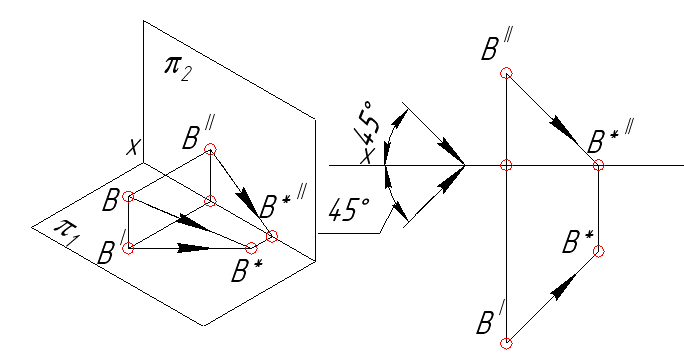
Рис. 43. Тень от точки падает на горизонтальную плоскость проекций p₁

Точка С является пограничной точкой (точкой излома тени). Тень от точки С падает на ось X.

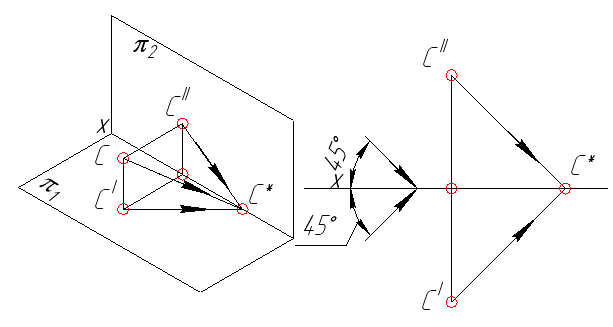
Рис. 44. Тень от точки падает на ось ^ Х

Мнимая тень точки А – (А*) находится на плоскости p₁, но за осью Х, то есть во второй четверти проекционного пространства. Действительной тенью точки А будет являться точка А*, лежащая на плоскости p₂.

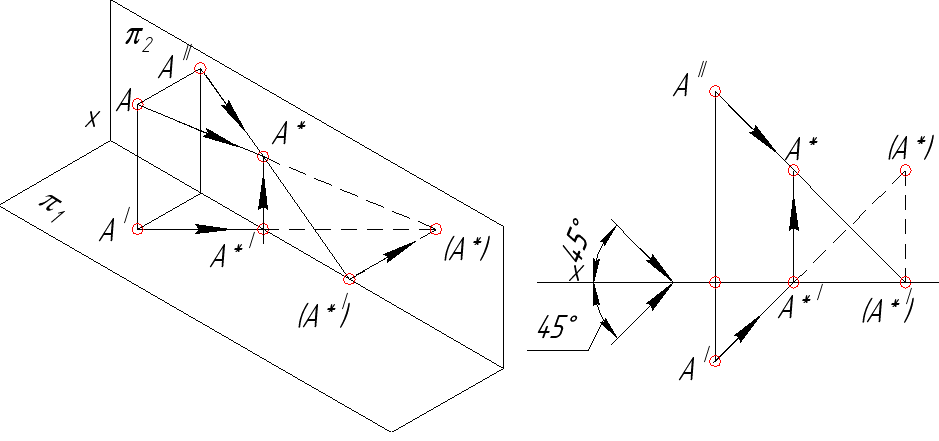
Рис. 45. Тень от точки падает на фронтальную плоскость проекций p₂

Очень часто тень от точки падает не на плоскости проекций, а на плоскости общего положения. В этом случае определение положения тени точки сводится к решению задачи, рассмотренной на лекции 2 (рис. 6). Через точку А (рис. 46) проводят световой луч и находят точку пересечения этого луча с плоскостью общего положения АВСD. Для этого через световой луч проводят плоскость частного положения, например, горизонтально проецирующую плоскость α. Строят линию пересечения плоскости заданной – BCDE и плоскости дополнительной – α. Линия 12 – линия пересечения двух плоскостей. Точка пересечения светового луча с линией 12 и является тенью точки на плоскости общего положения.

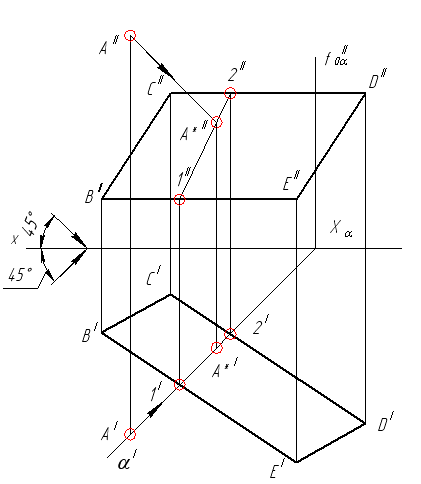
Рис. 46. Тень от точки А на плоскость общего положения

На рис. 47 представлен эпюр построения падающей тени при стандартном освещении прямой общего положения EF. Точка K - точка излома тени. Следует отметить соответствие построения теней точек Е и F (рис. 47) теням точек А (рис. 45) и B (рис. 43).

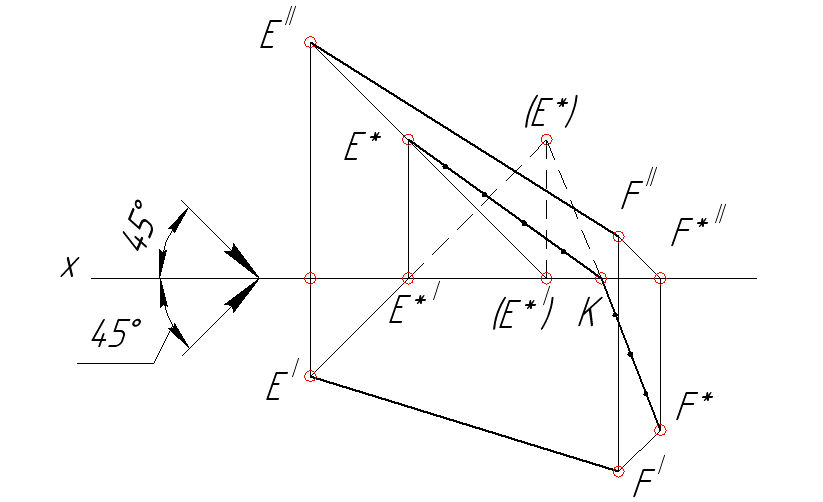
Рис. 47. Эпюр построения тени отрезка

Аналогично можно построить тень от любой плоской фигуры, например, от треугольника ^ АВС (рис. 48). Строим тень от каждой вершины треугольника. Соединив мнимые тени точек А и В с тень точки С, получим тень треугольника на горизонтальной плоскости проекций. На пересечении этой тени с осью X находим точки перелома тени – K и L.

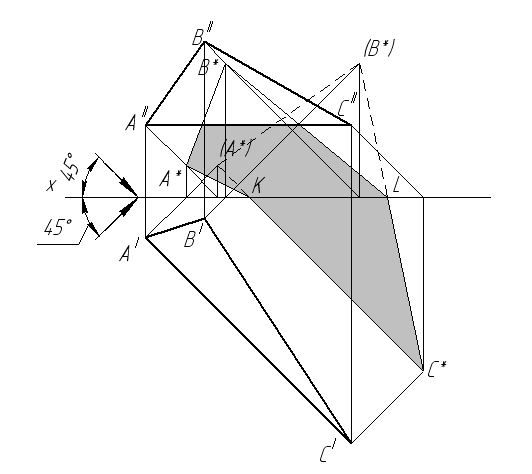
Рис. 48. Построение тени плоскости треугольника на плоскости проекций

ТЕНИ В ПЕРСПЕКТИВЕ

Изображение теней придает перспективе дополнительную выразительность и объемность. Направление световых лучей в отличие от комплексного чертежа может быть произвольным. При этом возможны три случая расположения параллельных световых лучей, идущих от солнца: лучи направлены от наблюдателя к объекту, лучи направлены от объекта к наблюдателю, лучи параллельны картинной плоскости (фронтальное положение лучей). При этом угол наклона лучей может быть произвольным в каждом из этих случаев. Для построения теней в перспективе необходимо знать перспективную проекцию луча, а также его вторичную перспективную проекцию. На рис.8.1 – 8.3 показано построение теней на предметную плоскость от горизонтального отрезка в каждом из вышеперечисленных случаев. Параллельные лучи будут иметь общую точку схода. Точка схода вторичных проекций лучей F₁^т находится на линии горизонта. Точка схода перспективной проекции лучей F^т в первом случае находится ниже линии горизонта (рис.8.1), во втором случае (рис.8.2) – выше линии горизонта, в третьем случае (рис.8.3) – точка схода отсутствует. Перспективная проекция тени A^т от точки A находится в пересечении вторичной проекции светового луча, направленного из вторичной проекции точки A₁^/ в точку схода F₁^т, с перспективной проекцией светового луча, направленного из точки A^/ в точку схода F^т. Аналогичным образом строится тень от точки B, что позволяет построить тень от отрезка по двум точкам.

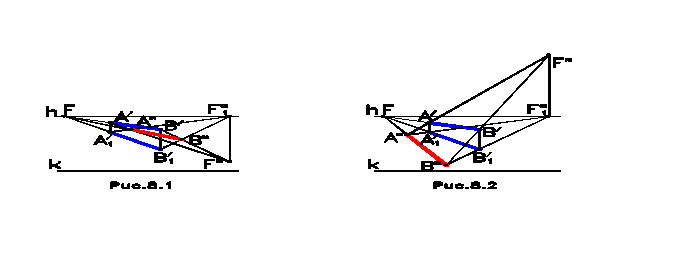
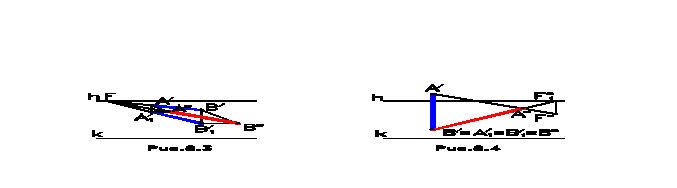
Тень от горизонтальной прямой AB на горизонтальную плоскость также является горизонтальной прямой A^тB^т, которая параллельна исходному отрезку AB, и следовательно, имеет ту же точку схода F. Тень от вертикальной прямой на горизонтальную плоскость совпадает с направлением вторичной проекции светового луча (рис.8.4).

На практике чаще всего используется первый случай направления световых лучей, т.к. большая часть объекта в этом случае освещена и перспектива выглядит наиболее выразительно.

Из всех способов построения теней, известных по теням на комплексном чертеже, в перспективе используются только два: способ лучевых сечений и способ обратных лучей. Остальные способы не используются, т.к. приводят к сложным построениям.

Последовательность построения теней такая же, как и на комплексном чертеже: выявляется контур собственной тени, затем строится падающая тень от контура собственной тени каждого геометрического образа на предметную плоскость (на комплексном чертеже на стену), затем падающие тени от одного геометрического образа на другой.

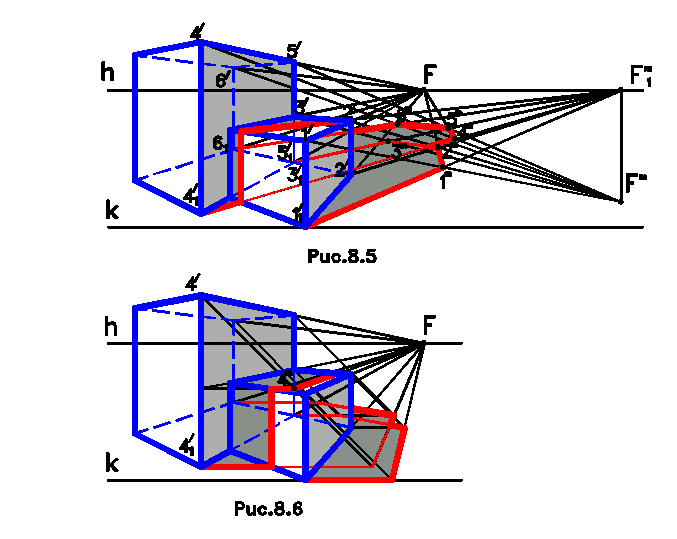
На рис.8.5 показано построение теней на примере двух параллелепипедов. От контура собственной тени 1^/ - 2^/ - 3^/ - 1₁^/ - 2₁^/ -3₁^/ малого параллелепипеда построена тень на предметную плоскость как от вертикальных и горизонтальных прямых. Затем построена тень от контура собственной тени 4^/ - 5^/ - 6^/ - 4₁^/ - 5₁^/ - 6₁^/ большого параллелепипеда на предметную плоскость. Контуром падающей тени обоих параллелепипедов является огибающий контур обеих теней. Кроме того, тень от большого параллелепипеда падает на верхнюю горизонтальную и переднюю вертикальную грани малого параллелепипеда. Для этого строятся лучевые сечения малого параллелепипеда, полученные от пересечения лучевых плоскостей, проведенных через контур собственных теней большого параллелепипеда. Такая лучевая плоскость проведена через ребро 4^/ - 4₁^/большого параллелепипеда, и она пересекла малый параллелепипед по сечению, которое является контуром падающей. Другие участки собственной тени большого параллелепипеда дают тени только на предметную плоскость. На рис.8.6 построены тени от тех же параллелепипедов при фронтальном положении лучей.