Монотонные последовательности
Последовательность чисел  называется неубывающей (возрастающей), если каждый последующий член последовательности не меньше (больше) предыдущего члена, т.е.
называется неубывающей (возрастающей), если каждый последующий член последовательности не меньше (больше) предыдущего члена, т.е.
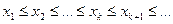
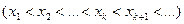 .
.
Если же каждый последующий член последовательности не больше (меньше) предыдущего члена, то последовательность называется невозрастающей (убывающей), т.е.
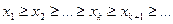
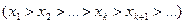 .
.
Эти четыре типа последовательностей называются монотонными.
Последовательность  , где
, где 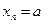 при всех
при всех 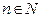 , называется стационарной. Стационарная последовательность является неубывающей, а также невозрастающей.
, называется стационарной. Стационарная последовательность является неубывающей, а также невозрастающей.
Чтобы установить, что последовательность  , например, убывает, достаточно доказать, что неравенство
, например, убывает, достаточно доказать, что неравенство 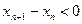 при всех
при всех 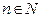 . Если же члены последовательности положительны, то последовательность будет убывать, если неравенство
. Если же члены последовательности положительны, то последовательность будет убывать, если неравенство 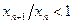 при всех
при всех 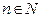 .
.
Свойство точных граней монотонных
последовательностей
1.Число  является точной верхней гранью неубывающей или возрастающей последовательности
является точной верхней гранью неубывающей или возрастающей последовательности  тогда и только тогда для каждого
тогда и только тогда для каждого 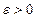 неравенство
неравенство 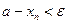 справедливо при всех
справедливо при всех 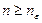 .
.
2. Число  является точной нижней гранью невозрастающей или убывающей последовательности
является точной нижней гранью невозрастающей или убывающей последовательности  , тогда и только тогда, когда для каждого
, тогда и только тогда, когда для каждого 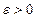 неравенство
неравенство 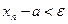 справедливо при всех
справедливо при всех 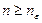 .
.
Доказательство.
1.Пусть  является точной верхней гранью неубывающей или возрастающей последовательности
является точной верхней гранью неубывающей или возрастающей последовательности  , т.е.
, т.е. 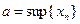 . Тогда имеем цепочку равносильных утверждений:
. Тогда имеем цепочку равносильных утверждений: 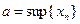
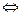
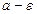 не является верхней гранью множества
не является верхней гранью множества 
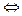
 содержит такой элемент
содержит такой элемент 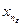 , для которого
, для которого 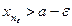
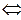
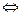
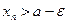 , если
, если 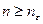 (так как последовательность
(так как последовательность  неубывающая или возрастающая, то
неубывающая или возрастающая, то 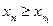 , если
, если 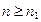 ).
).
2. Случай невозрастающей или убывающей последовательности рассматривается аналогично. ■
Примеры.
2.1.Доказать, чтоследующие последовательности  являются монотонными и найти их точные грани:
являются монотонными и найти их точные грани:
а) 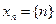 ; б)
; б) 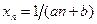 ; в)
; в) 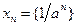 ; г)
; г) 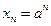 ; д)
; д) 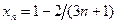 .
.
Решение
а)Последовательность 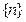 является возрастающей, так как последующий член больше предыдущего. Эта последовательность неограниченна сверху, так как неравенство
является возрастающей, так как последующий член больше предыдущего. Эта последовательность неограниченна сверху, так как неравенство 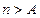 выполняется при всех
выполняется при всех 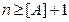 . Следовательно, эта последовательность не имеет точной верхней грани. Элемент
. Следовательно, эта последовательность не имеет точной верхней грани. Элемент 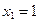 является наименьшим ее элементом.
является наименьшим ее элементом.
б) Последовательность 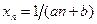 ,
, 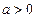 и
и 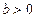 , является убывающей, так как для всех
, является убывающей, так как для всех 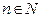 имеем:
имеем:
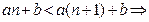
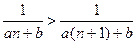 .
.
Отсюда следует, что элемент 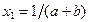 является наибольшим элементом последовательности.
является наибольшим элементом последовательности.
Докажем, что 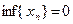 , т.е. для каждого
, т.е. для каждого 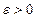 неравенство
неравенство 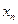
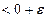 справедливо при всех
справедливо при всех  (свойство 2 в § 2.2). Имеем:
(свойство 2 в § 2.2). Имеем:
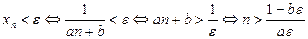
Из теоремы 2.1 следует, что неравенство 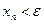 справедливо при всех
справедливо при всех  .
.
в) Последовательность 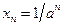 является убывающей, если
является убывающей, если 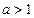 :
:
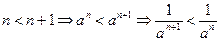 для всех
для всех 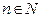 .
.
Следовательно, элемент 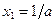 является наибольшим элементом.
является наибольшим элементом.
Докажем, что 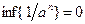 , т.е. для каждого
, т.е. для каждого 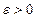 неравенство
неравенство 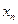
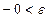 справедливо при всех
справедливо при всех  (свойство 2 в § 2.2). Имеем:
(свойство 2 в § 2.2). Имеем:
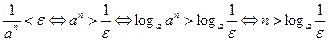 .
.
Из теоремы 2.1 следует, что неравенство 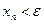 справедливо при всех
справедливо при всех  .
.
г) Последовательность 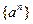 , является возрастающей, если
, является возрастающей, если 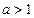 , так как последующий член больше предыдущего. Она неограниченна сверху, так как неравенство
, так как последующий член больше предыдущего. Она неограниченна сверху, так как неравенство 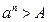 выполняется при всех
выполняется при всех 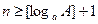 , поэтому последовательность
, поэтому последовательность 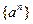 не имеет точной верхней грани. Элемент
не имеет точной верхней грани. Элемент 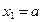 является наименьшим ее элементом.
является наименьшим ее элементом.
д) Последовательность 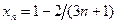 является возрастающей, так как для всех
является возрастающей, так как для всех 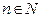 имеем:
имеем:
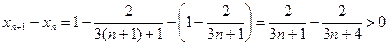 ,
,
поэтому элемент 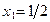 является ее наименьшим элементом.
является ее наименьшим элементом.
Докажем, что 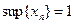 , т.е. для каждого
, т.е. для каждого 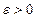 неравенство
неравенство 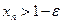 справедливо при всех
справедливо при всех  (свойство 2 в § 2.2). Имеем:
(свойство 2 в § 2.2). Имеем:
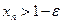
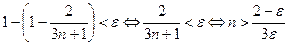 .
.
Из теоремы 2.1 следует, что неравенство 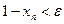 справедливо при всех
справедливо при всех  .
.
2.2. Найти такое натуральное число 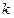 , что при всех
, что при всех 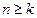 последовательность
последовательность 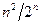 убывает.
убывает.
Решение. Имеем следующую цепочку равносильных утверждений:
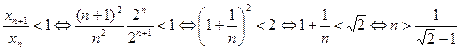 .
.
Последнее утверждение в этой цепочке является истиной при всех 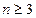 . Следовательно, отношение
. Следовательно, отношение 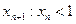 также является истиной при всех
также является истиной при всех 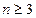 , поэтому последовательность
, поэтому последовательность 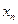 является убывающей при всех
является убывающей при всех 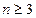 . ●
. ●
Теорема 2.2.Каждая числовая последовательность  либо содержит убывающую, либо содержит неубывающую подпоследовательность.
либо содержит убывающую, либо содержит неубывающую подпоследовательность.
Доказательство.Назовем элемент 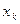 последовательности
последовательности  правильным, если все последующие члены последовательности меньше
правильным, если все последующие члены последовательности меньше 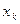 . Если элемент
. Если элемент 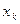 не является правильным, то будем называть его неправильным.
не является правильным, то будем называть его неправильным.
Если правильных элементов бесконечно много, то они образуют убывающую подпоследовательность: если 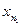 и
и 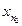 — правильные элементы и
— правильные элементы и 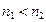 , то
, то 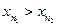 , так как
, так как 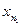 правильный элемент.
правильный элемент.
Если же правильных элементов конечное множество, то обозначим через 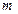 наибольший номер этих элементов. Тогда все элементы последовательности, номера которых больше
наибольший номер этих элементов. Тогда все элементы последовательности, номера которых больше 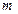 , являются неправильными.
, являются неправильными.
Рассмотрим неправильный элемент 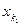 ,
, 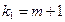 . Так как
. Так как 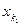 — неправильный элемент, то среди следующих за ним элементов найдется такой элемент
— неправильный элемент, то среди следующих за ним элементов найдется такой элемент 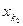 , что
, что 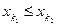 ,
, 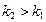 . Элемент
. Элемент 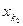 тоже неправильный (
тоже неправильный ( 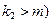 и среди следующих за этим элементов найдется такой элемент
и среди следующих за этим элементов найдется такой элемент 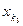 , что
, что 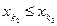
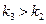 . Продолжая процесс построения элементов таким образом далее, получим неубывающую подпоследовательность
. Продолжая процесс построения элементов таким образом далее, получим неубывающую подпоследовательность 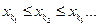 .■
.■
Задачи
2.1. Доказать монотонность последовательностей:
а) 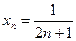 , б)
, б) 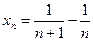 , в)
, в) 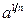 , г)
, г) 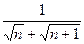 .
.
2.2. Найти точные грани следующих последовательностей  :
:
a) 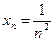 ; б)
; б) 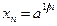 ; в)
; в) 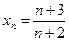 .
.
2.3. Найти точную верхнюю грань следующих последовательностей:
а) 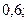
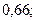
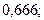
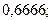
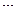 ;
;
б) 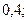
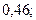
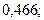
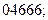
 .
.
(Указание: представить 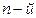 член последовательности в виде суммы
член последовательности в виде суммы 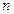 слагаемых).
слагаемых).
2.4. Найти такое натуральное число 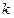 , чтобы при всех
, чтобы при всех 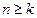 последовательность
последовательность  была монотонной:
была монотонной:
a) 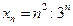 , б)
, б) 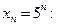
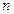 !.
!.
2.5. Доказать, что каждая последовательность содержит либо возрастающую последовательность, либо невозрастающую последовательность.
Дата добавления: 2016-06-05; просмотров: 4652;











