Состояние горных пород в земной коре

Давление вышележащих пород и тектонические процессы, протекающие в земной коре, оказывают значительное влияние на напряженное состояние горных пород.

Поэтому сведения об упругих и прочностных свойствах горных пород, определяемых при простых видах деформации, только в некоторых случаях могут быть применимы к условиям разрушения пород в процессе бурения скважин.

В реальных условиях разрушаемые во время бурения горные породы находятся в более сложном, чем при простых видах деформации, напряженном состоянии. Поэтому изучение механических свойств пород в условиях сложного всестороннего сжатия имеет большое практическое значение.

Исследование поведения горных пород в условиях всестороннего сжатия проводится с помощью приборов или установок, рассчитанных на высокие давления. Такие приборы состоят из цилиндра или «бомбы», внутри которых размещается исследуемый образец горной породы в виде или керна или прямоугольной призмы. Всестороннее давление на образец создается жидкостью, нагнетаемой в цилиндр или «бомбу».

При отсутствии тектонических движений на участке земной коры напряженное состояние горных пород осесемметрично относительно вертикали. Это позволяет охарактеризовать напряженное состояние горных пород двумя величинами в цилиндрической системе координат:

s_z = s_з и s_z = =s₁ = s₂

Вертикальные напряжения s_z зависят от веса вышележащих пород, поэтому можно записать:

s_z = - g_z,

где g - средняя плотность вышележащих пород;

z - глубина залегания пород.

В процессе сжатия вертикальным давлением горные породы в поперечном направлении деформируются не свободно. В этом случае имеет место равенство :

.

Отсюда получим:

.

Подставив значение s_z, получим формулу для упругого напряженного состояния горных пород:

.

В общем случае эта формула будет иметь вид:

.

Величина l называется коэффициентом бокового распора.

Если учесть явление релаксации, т. е. выравнивание напряжения в земной коре, то l ® 1.

В большинстве случаев можно принять, что l = 1 и s_z = s_r.

Это условие равномерного всестороннего сжатия. Напряженное состояние в этом случае будет характеризоваться средним нормальным напряжением: s₀ = s_z = s_r ,

Естественное напряжение в земной коре принято называть горнымдавлением.

Вертикальную составляющую горного давления s_z называют геостатическим или полным горным давлением,а горизонтальную составляющую s_r - боковым давлением.

Горные породы, обладающие той или иной пористостью, всегда насыщены жидкостью или газом. Давление поровой жидкости принято называть пластовымдавлением.

В нормальных условиях пластовое давление (Р) приблизительно равно гидростатическому давлению воды, т. е. Р = gвz,

Однако, возможность встречи с аномально высоким пластовым давлением с глубиной залегания увеличивается, особенно в районах активной тектонической деятельности.

Каким же образом давление жидкости в порах влияет на напряженное состояние горной породы?

За идеальную модель пористого тела прием тело с круглыми отверстиями. Вырежем единичный элемент в виде, представленном на рисунке. Сверху на эту элементарную площадь действует геостатическое давление

Р_г = gz,

Если бы все вертикальное давление воспринималось скелетом породы, то напряжение в скелете в сечении 1-1 было бы максимальным и равным

,

где Р_г - горное давление;

n Р - пластовое давление;

n - часть единичной площади, занимаемой скелетом в сечении 1-1.

Учитывая то, что поровая жидкость воспринимает на себя часть нагрузки, равной Р(1 - n), то напряжение в скелете породы будет выражаться формулой

. Если обозначить , тогда можно записать: . Совершенно очевидно, что h зависит от пористости и структуры порового пространства.

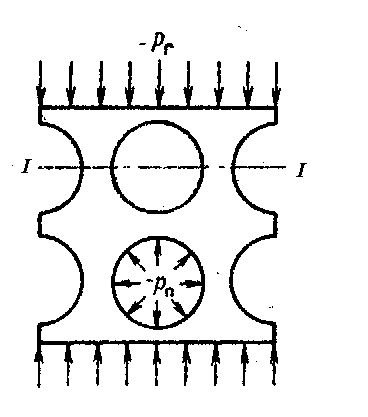Рис.19 Модель пористой породы

Из последней формулы можно сделать вывод, что с увеличением пластового давления Р наблюдается уменьшение вертикальной нагрузки на скелет. В случае, если Р = Р_г, то

s_с = - Р_г,

где Р_г - геостатическое или полное горное давление.

Следовательно, по мере приближения пластового давления Р к геостатическому напряженное состояние скелета стремится к равномерному всестороннему сжатию.