ВИДЫ ДЕФОРМАЦИЙ ГРУНТОВ И ПРИЧИНЫ, ИХ ОБУСЛОВЛИВАЮЩИЕ
Определение деформаций грунтов под действием внешних сил имеет огромное значение для практики проектирования фундаментов сооружений.
Факторами, определяющими долговечность сооружений, собственно говоря, являются не напряжения в грунте (если они не до- стигают предельных величин), а деформации оснований, их осадки, под которыми понимают обычно вертикальные смещения грун- товых оснований. Однако равномерная осадка всего сооружения не вызывает дополнительных напряжений в его конструкциях, но разность осадок отдельных частей основания Особенно сказывается на прочности фундаментов и над фундаментных строений. А так как разность осадок оснований, как показывают соответствующие наблюдения в натуре, как правило, бывает тем больше, чем больше абсолютная осадка оснований, то важно знать как величину абсо- лютной осадки, так и разности осадок отдельных частей сооруже- ний.
За последние десятилетия на базе развития теории расчета осадок грунтовых оснований (главным образом отечественными учеными) И статистической обработки результатов многочисленных замеров осадок и разности осадок различного рода сооружений нд различных напластованиях грунтов оказалось возможным разработать наиболее прогрессивный метод расчета фундаментов по предельным деформациям оснований, который при полной гарантии безопасности дает и. значительный экономический эффект.
Этот метод, в настоящее время широко применяемый в отечественной проектной практике, базируется на обязательном соблю- дении следующих основных условий:
Зрасч =S^ SnpJ I ASpac4 Sj ASnp,'
анализа результатов многочисленных наблюдений за осадками оснований сооружений и регламентируемых соответствующими нормами СНиПа.
Грунты, как было рассмотрено ранее (см. гл. II, § 4), являются сложными многофазными системами частиц, деформации которых зависят как от общего изменения их объема (уплотнения, набухания и пр.), так и от деформируемости всех компонентов (фаз), составляющих грунты (ползучести скелета, сжимаемости поровой воды, а также включений паров и газов и пр.), и их взаимодействия.
Различные виды деформаций грунтов и причины, их вызывающие, систематизированы нами в табл. 24.
Таблица 24 Главнейшие физические причины деформаций грунтов
Вид деформаций Причины деформаций
Упругие:
изменения объема Молекулярные силы упругости твердых частиц,
а также тонких пленок воды и замкнутых пузырьков воздуха
искажения формы Молекулярные силы упругости, искажение струк
турной решетки
Неупругие остаточные:
уплотнения Уменьшение пористости (компрессионные свой
ства)
набухания Расклинивающий эффект как результат действия
электромолекулярных сил ползучести Взаимные сдвиги частиц
чисто остаточные Разрушение структуры, излом частиц
На практике в одних случаях имеют первостепенное значение упругие деформации, например при динамических нагрузках (включая и сейсмические воздействия) и при расчете гибких фундаментов на совместную работу их со сжимаемым основанием, в других — неупругие (уплотнения и набухания) — при расчете, главным образом, массивных фундаментов по предельным деформациям оснований (для определения величины полной осадки грунтовых оснований и затухания осадок во времени), а иногда — чисто остаточные (при образовании колей на усовершенствованных грунтовых покрытиях и дорогах) и т. п.
§ 2. УПРУГИЕ ДЕФОРМАЦИИ ГРУНТОВ И МЕТОДЫ ИХ ОПРЕДЕЛЕНИЯ
Условия возникновения упругих деформаций в грунтах. Хотя упругость w является общим свойством всех тел природы, но грунты, представляющие собой сложные дисперсные природные образо

для вертикальных перемещений точек, лежащих на ограничивающей полупространство плоскости (z=0) при действии на полупространство сосредоточенной силы Р [см. гл. Ill, § 1, формула (III.3)]:
где коэффициент упругого полупространства
Отметим, что если рассматривается линейно деформируемое полупространство, то модуль упругости грунта Е следует заменить на модуль общей деформации (упругой и остаточной) Е0, а коэффициент Пуассона у —на коэффициент общей относительной поперечной деформации ц0.
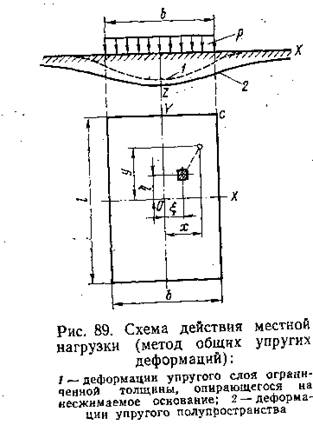
При действии на ограничивающую упругое полупространство плоскость местной равномерно распределенной по площадке F нагрузки р осадки любой точки определятся путем интегрирования выражения для вертикальных перемещений точки упругого полупространства от действия элементарной сосредоточенной силы pd^dr\ (рис. 89),
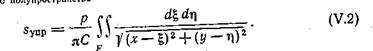
|
Обозначив координаты рассматриваемой точки через хну и используя формулу (Ш.З), получим
|

|
мы площади подошвы и местоположения рассматриваемой точки (легко табулируемый).
Выражение (V:3) показывает, что осадки однородного упругого (или линейно деформируемого) полупространства прямо пропорциональны (со’/С — коэффициент пропорциональности) удельному давлению на грунт р и корню квадратному из площади У F.
Важно отметить, что опыты в натуре по изучению осадок грунтовых оснований для площадей от 0,5 до 15 м2 на однородном водонасыщенном заиленном песке мощностью около 12 м (опыты X- Р. Хакимова, 1939 г. и др.), а также опыты «Фундаментстроя» (Д. Е. Польшина и др.) на лёссовидных однородных суглинках с площадями от 0,25 до 8 м2 в пределах линейной связи между давлением и осадкой дают следующую эмпирическую зависимость:
Таким образом, теоретическая формула (V.3) при внешнем давлении, не превышающем практического предела пропорциональности, для грунтов, однородных на достаточную глубину, в общем виде полностью подтверждается опытами (хотя коэффициент пропорциональности А в некоторых случаях несколько отличается от теоретического ш'/С).
Однако зависимость осадки от величины площади загрузки, как показывают опыты в природных условиях, при большом диапазон изменения площадей выражается более сложной зависимостью.
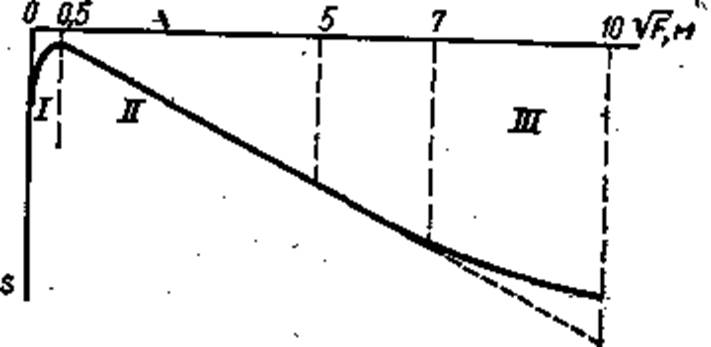
Так, на рис. 90 приведена обобщенная кривая средних результатов многочисленных опытов по изучению осадок
грунтовых оснований (примерно средней их уплотненности) при одном и том же давлении на грунт, но при разной величине площади загрузки. На этой кривой можно, различать три области: область / — малых площадей загрузки (примерно до 0,25 л*?), где при средних давлениях грунты находятся преимущественно в фазе сдвигов, причем наблюдается уменьшение осадки е увеличением площади (как раз обратное тому, что дает теория упругости для фазы ли-
нейных деформаций); область II—при площадях от 0,25-^0,50 до 25-1-50 м2 (для однородных грунтов средней плотности, а для слабых грунтовки до больших величин), где осадки строго пропорциональны V F и соответствуют при средних давлениях на грунт фазе уплотнения, т. е. весьма близки к теоретическим-, область III — для площадей, больших 25-1-50 м2, где осадки меньше теоретических, что можно объяснить возрастанием модуля упругости (уменьщением деформируемости) грунтов с глубиной. Конечно, для очень
|
Рис. 90. Зависимость осадки природных грунтов от размеров площади загрузки
рыхлых и очень плотных грунтов указанные пределы будут несколько иными.
Приведенные данные могут служить для установления пределов применимости теоретических решений, полученных для однородных массивов, к реальным грунтам, что имеет особо важное значение при разработке рациональных методов расчета осадок оснований сооружений.
Основной зависимости осадки от величины площади загрузки и действующего внешнего давления (формула (V.3)] для удобства дальнейшего использования придадим иной вид (ставший в настоящее время уже общепринятым), введя отношение длины к ширине сторон прямоугольной площади загрузки а — 1/Ь_(а следовательно, l — ab и F = ab2) и обозначив через со величину со'У а:
s™ =. (V.4)
учр------- ^ >
где © — коэффициент формы площади подошвы и жесткости
фундамента (одинаковый для всей площади загрузки или различный для разных ее точек);
в— ширина прямоугольной площади подошвы или диаметр
круглой;
р — удельное давление на грунт;
Е, ц — модули упругости (деформируемости) полупространства.
Для облегчения расчетов приведем в табл. 25 ряд значений коэффициента формы © для круга и прямоугольников с различным отношением сторон a=ilib (где I — длина, b — ширина прямоуголь-
ной площади подошвы).
Отметим, что формула (V.4) используется обычно и для опытного определения по результатам полевой пробной нагрузки (площадкой в 5000 см2) модуля общей деформации грунта Е0 кГ/см2.
Придав обозначениям для модулей общей деформируемости букву «о» в индексе, из формулы (V.4) получим
| <opb( 1 |
| Е0 |
| ’ |Ао) |
| So |
где S0-общая осадка штампа (остаточная и упругая), но в пределах линейной зависимости между осадками s0 и давлением р. .
Обычно величиной коэффициента относительной поперечной деформации ро задаются, принимая ее согласно опытным данным равной: для глин и суглинков твердых и полутвердых ро = 0,1—0,15; тугопластичных — р0 = 0,20-^0,25; пластичных и текучепластичных— р0=0,30-^0,40 и текучих —р0 = 0,45-^0,50; для супеси (в зависимости от консистенции) ро=0,15^0,30; для песков ро=0,20-ь -г-0,25.
Ранее [гл. II, формула (11.37)] было принято
Е -1
"О---- >
а0
где а0 — коэффициент относительной сжимаемости грунта;
Р — коэффициент, характеризующий боковое расширение грунта (функция р0).
Коэффициент р определим исходя из следующего. Как известно из курса сопротивления материалов, относительная деформация ez линейно деформируемой элементарной призмы при действии сжимающих напряжений по трем взаимно перпендикулярным направлениям будет равна
ez = jy-(o* + оу). (щ)
■Со Со
А так как в условиях невозможности бокового расширения грунта при сплошной нагрузке
Ох — Оу —
Цо
(Хо
-р И Oz — р, ТО
= -f (I—r^-)
С0 \ 1 — р0 /
(н2)
Множитель, стоящий в скобках, обозначают обычно р, т. е.
Р=1
2р0
1 — Цо
А так как по формуле (П.5') а0 =, то из выражения (н2) получим формулу (П.З?'):
ez
hp
(V.5)
Е0 =
1_
а0
Деформации упругого полупространства при действии местной нагрузки возникают не только непосредственно под нагрузкой (по ее подошве), но распространяются в стороны на значительные от нее расстояния, образуя «упругую лунку» (см. рис. 89). Опыты, однако, показывают, что в реальных грунтовых условиях «упругая лунка» под нагрузкой имеет значительно меньшее распространение, чем по решению теории упругого полупространства. Последнее, по- видимому, следует объяснить тем, что в работу грунта под нагрузкой включается практически далеко не весь массив грунта (полупространство), а лишь ограниченная его область.
Изложенное положение, а также в ряде случаев практики фактическое неглубокое залегание несжимаёмых скальных пород побудило ставить и решать задачу1 о напряжениях и деформациях упругого слоя ограниченной толщины, подстилаемого недеформируе- мым скальным основанием. Решению этой задачи посвящен ряд работ как отечественных ученых (М. И. Горбунова-Посадова, О. Я. Шехтер, К. К. Егорова и др.), так и зарубежных (Маргера, Совинца и др.).
. М. И. Горбунов-Посадов получил решение рассматриваемой задачи методом приближенного интегрирования общего уравнения деформаций и определения значений ряда коэффициентов мть, средних для всей площади загрузки при различной глубине слоя сжимаемого грунта h, выраженной в долях от ширины нагрузки Ь
(см.табл.25).
Таблица 25
Дата добавления: 2016-06-05; просмотров: 5921;











