Классификация систем нечеткой логики

Системами нечеткой логики называются системы, которые оперируют с нечеткими понятиями, такими как нечеткие множества, лингвистические переменные и т.п., и используют при этом нечеткую логику. Системы нечеткой логики могут быть классифицированы по трем основным типам:

1) простые системы нечеткой логики (pure Fuzzy Logic Systems);

2) нечеткие системы Такаги и Суджено (Takagi and Sugeno);

3) системы нечеткой логики с фаззификатором и дефаззификатором.
Простые системы нечеткой логики. Базовая конфигурация простой системы нечеткой логики представлена на рисунке.

Базис нечетких правил содержит набор нечетких IF-THEN (ЕСЛИ-TO) правил, а механизм нечеткого вывода на основе принципов нечеткой логики использует эти IF-THEN-правила для отображения нечетких множеств из входящего множества высказываний Х в нечеткие множества из множества высказываний Y на выходе системы.

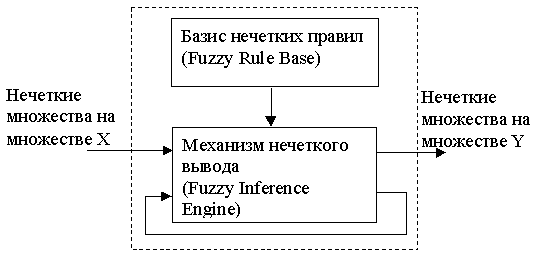
Рисунок - Простая система нечеткой логики

Практика показывает, что эти нечеткие IF-THEN-правила обеспечивают удобный механизм для представления знаний человека-эксперта.

Если присутствует обратная связь, как показано на рисунке, то мы имеем так называемую нечеткую динамическую систему, т.е. простую систему нечеткой логики, у которой входы зависят от ее выходов. Структура простой системы нечеткой логики является существенной частью систем нечеткой логики. В общем случае, когда лингвистическая информация от эксперта переводится в количественные показатели, принципы нечеткой логики используются для систематизации информации.

Главным недостатком простых систем нечеткой логики является то обстоятельство, что ее входы и выходы - нечеткие множества, тогда как в большинстве технических систем входы и выходы являются переменными, принимающими реальные значения.

Нечеткие системы Такаги и Суджено. Такаги и Суджено предложили использовать IF-THEN-правила:

L^(p): IF x₁ есть F₁^p и . . . и x_n есть F_n^p THEN y^p = C₀^p + C₁^p x₁ +. . .+ C_n^p x_n,

где F_i^p - нечеткие множества;

С_i - параметры, принимающие реальные значения;

y^p - выход системы, соответствующий правилу L^(p); p= .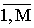

Таким образом, они рассматривали правила, у которых часть IF является нечеткой, но "четкой" является часть THEN, и выход является линейной комбинацией переменных на входе. Выход нечеткой системы Такаги-Суджено есть взвешенное среднее:

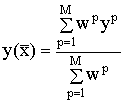
где вес w^p вычисляется как:

Конфигурация нечеткой системы Такаги-Суджено представлена на рисунке.

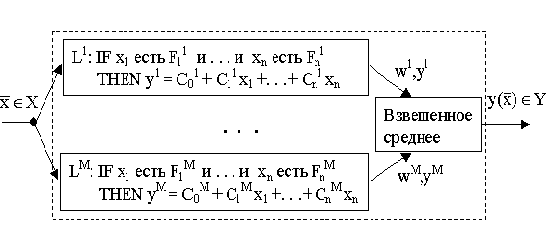
Рисунок - Система нечеткой логики Такаги-Суджено

Преимуществом систем нечеткой логики такого типа является то, что они описываются компактной системой уравнений. Для них могут быть легко разработаны методы оценки параметров и выбора порядка системы М.

Слабое место таких систем нечеткой логики заключается в том, что часть THEN в IF-THEN-правиле не является нечеткой, что не позволяет естественным образом получать нечеткие правила от человека-эксперта.