Преобразование схем

В частном случае, когда схема замещения не содержит множество замкнутых контуров и в этой схеме имеется один или несколько источников с одинаковыми ЭДС, ее можно легко привести к простейшему виду (результирующий (эквивалентный) источник ЭДС Е_S - результирующее сопротивление х_S - точка КЗ), приведенному на рис. 2.4.

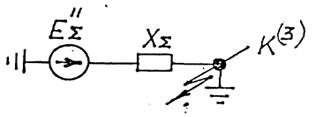
Рис. 2.4. Результирующая схема замещения, эквивалентная схеме, приведенной на рис. 2.2

Из этой схемы легко определить действующее значение периодической (вынужденной) составляющей тока трехфазного КЗ в нулевой момент времени:

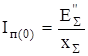. (2.1)

Схема на рис. 2.4 получается путем последовательного и параллельного сложения элементов.

Приведение более сложных схем к простейшему виду требуют дополнительных преобразований:

1) треугольника в звезду и наоборот;

2) многолучевой звезды в полный многоугольник;

3) "разрезание" треугольника с ЭДС, подключенной к вершине, по данному узлу;

4) замены нескольких генерирующих ветвей с разными по величине ЭДС, присоединенных к общему узлу, одной эквивалентной.

Разберем эти преобразования. При последовательном соединении n элементов эквивалентное сопротивление равно:

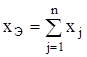. (2.2)

При параллельном соединении n элементов:

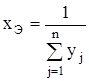. (2.3)

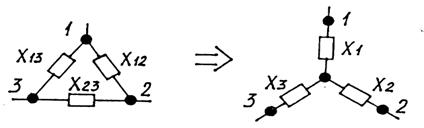
Рис. 2.5. Схемы преобразования из треугольника в эквивалентную звезду

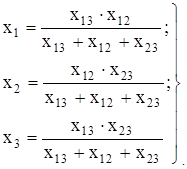(2.4)

Если требуется обратное преобразование, то формулы будут следующие:

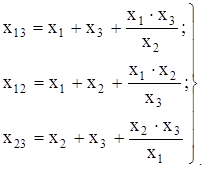(2.5)

При преобразовании многолучевой звезды в эквивалентный полный многоугольник:

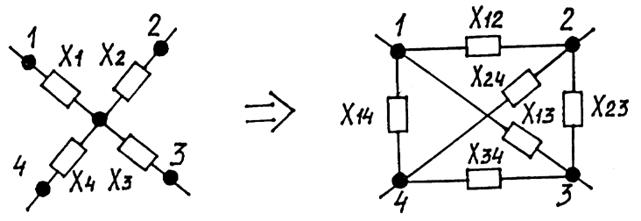
Рис. 2.6. Схемы преобразования из многолучевой звезды в эквивалентный полный многоугольник (с диагоналями)

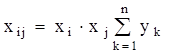. (2.6)

Например, необходимо определить сопротивления х₁₃ и х₁₂:

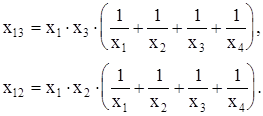
Таким образом определяются все сопротивления полного многоугольника.

Часто используется преобразование звезды с ЭДС в треугольник с последующим "разрезанием" узла (узлов) с ЭДС. Рассмотрим этот случай.

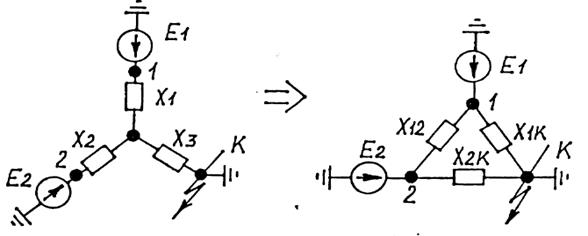
Рис. 2.7. Преобразование звезды в треугольник

После такого преобразования (см. рис. 2.7), "разрежем" по узлам 1 и 2 и получим схему (см. рис. 2.8).

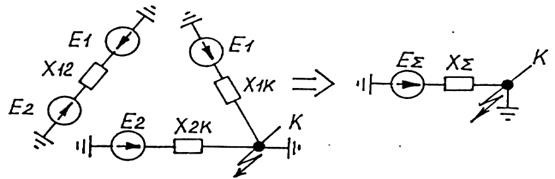
Рис. 2.8. Схема с "разрезанием" по узлам с ЭДС и последующим ее преобразованием к простейшему виду

Как видно из схемы, сопротивление х₁₂ никак не будет влиять на величину тока КЗ. Схема замещения теперь преобразуется к простейшему виду путем замены двух генерирующих ветвей с разными по величинам ЭДС, присоединенных к общему узлу К, одной эквивалентной - по формуле:

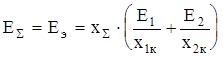, (2.7)

где 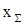- результирующее (эквивалентное) сопротивление двух параллельных ветвей х_S = х_1к · х_2к /(х_1к+х_2к).

Формулу (2.7) можно после преобразования записать (для двух параллельных ветвей):

.

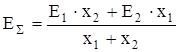В общем виде при n параллельных ветвях выражение эквивалентной ЭДС запишется:

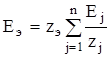, (2.8)

где 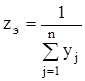- эквивалентное сопротивление параллельных ветвей.

Теперь преобразуем приведенную на рис. 2.9 схему замещения к простейшему виду, используя все рассмотренные виды преобразований (самостоятельно).

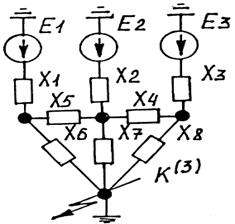
Рис. 2.9. Схема замещения, которую необходимо преобразовать к простейшему виду