Применение метода симметричных составляющих к расчету

Несимметричных КЗ

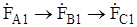С целью упрощения расчетов несимметричных режимов в трехфазной сети предложен метод симметричных составляющих. Любую несимметричную трехфазную систему векторов (токов, напряжений) можно представить в виде трех симметричных систем. Одна из них имеет прямую последовательность чередования фаз ( ), вторая - обратную ( ), а третья система называется системой нулевой последовательности, которая состоит из трех равных векторов, совпадающих по фазе . Указанные системы векторов приведены на рис. 8.2.

Рис. 8.2. Графическое определение полных фазных величин трехфазной несимметричной системы через известные симметричные составляющие прямой, обратной и нулевой последовательностей

Таким образом, для каждой фазы можно записать:

(8.1)

Если известны величины и направления векторов прямой, обратной и ну-

левой последовательностей фазы А, то можно записать:

В выражениях (8.2; 8.3; 8.4) a- оператор поворота единичного вектора, (в показательной форме он равен e^j120°, а в комплексном виде а= =-0,5+j0,87).

Умножение какого либо вектора на оператор а означает поворот первого на 120° против движения часовой стрелки. Если же вектор умножить на a², то это означает поворот первого на 240° против часовой стрелки. Основные свойства оператора а можно записать в следующем виде:

(8.5)

Из уравнений (8.2; 8.3; 8.4) видно, что при использовании метода симметричных составляющих достаточно вычислить значения симметричных составляющих только одной какой-либо фазы (как правило, фазы А), по которым вычисляются симметричные составляющие двух других фаз, а затем и полные значения соответствующих фазных величин:

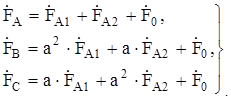(8.6)

Таким образом, вместо одной несимметричной схемы рассчитываются три, но значительно более простые, что дает существенное упрощение вычислений.

Симметричные составляющие любой из фаз можно получить, если будут известны полные фазные величины. Покажем это, например, для фазы А.

Выражение для определения составляющей нулевой последовательности получим путем сложения всех уравнений системы (8.6):

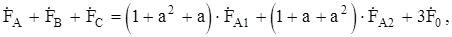
откуда

(8.7)

Для определения составляющей обратной последовательности 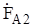второе и третье уравнения системы (8.6) умножим соответственно на а²и a и затем, сложив все три уравнения, получим:

(8.8)

Выражение для определения составляющей прямой последовательности 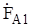получим путем умножения второго и третьего уравнений системы (8.6) соответственно на аиa² с последующим сложением уравнений (как в предыдущем случае):

(8.9)

Уравнения (8.7, 8.8, 8.9) дают возможность определения графическим путем по известной векторной диаграмме полных фазных величин фазные величины симметричных составляющих при анализе несимметричных режимов в аварийных ситуациях.

Геометрические суммы векторов прямой и обратной последовательностей всех трех фаз равны нулю, то есть эти системы являются уравновешен- ными, а система нулевой последовательности - неуравновешенная, так как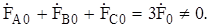

Несимметричные токи, протекающие по фазам трехфазной симметричной цепи, создают на сопротивлениях фаз несимметричные падения напряжения. Эти падения напряжения можно разложить на симметричные составляющие (в зависимости от вида КЗ):

(8.10)

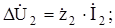(8.11)

(8.12)

где 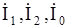- симметричные составляющие токов прямой, обратной и нулевой последовательностей соответственно;

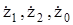- полные сопротивления соответственно прямой, обратной и нулевой последовательностей элемента электрической цепи. Величины этих сопротивлений в общем случае различны.

Протекающие по обмоткам статора генератора токи прямой, обратной и нулевой последовательностей создают магнитные потоки тех же последовательностей, а последние наводят в статоре соответствующие ЭДС. Вводить эти ЭДС в расчет нецелесообразно, так как они пропорциональны (в случае ненасыщенной магнитной системы) токам отдельных последовательностей, а их значения необходимо еще определить. Поэтому в расчет вводят только те ЭДС, которые известны или не зависят от внешних условий цепи статора генератора. Известными являются ЭДС только прямой последовательности. ЭДС, обусловленные токами обратной и нулевой последовательностей, вводят в схему замещения в виде падений напряжения на соответствующем сопротивлении генератора с обратным знаком [2].

В симметричных трехфазных цепях с ненасыщенными магнитными системами отдельных элементов может быть применен принцип наложения, предполагающий, что отдельные симметричные составляющие действуют независимо друг от друга [5]. Это обстоятельство позволяет составлять схемы замещения для каждой последовательности отдельно. Свернутые относительно точки КЗ эти результирующие схемы замещения приведены на рис. 8.3.

Рис. 8.3. Результирующие схемы замещения прямой (а), обратной (б) и нулевой (в) последовательностей

Обычно схемы замещения составляются для фазы А, которую называют особой фазой.

В соответствии со вторым законом Кирхгофа можно записать следующие выражения для определения симметричных составляющих напряжения в месте КЗ:

(8.13)

где 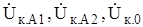- симметричные составляющие напряжения для фазы А в месте КЗ;

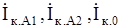- симметричные составляющие тока (за положительное направление принято направлять токи к точке КЗ);

- результирующие полные сопротивления прямой, обратной и нулевой последовательностей цепи КЗ;

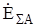- фазная эквивалентная суммарная ЭДС прямой последовательности источников, питающих цепь КЗ.

При симметричном металлическом трехфазном КЗ напряжение в месте повреждения равно нулю, то есть 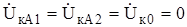, и при таком виде КЗ будут протекать только токи прямой последовательности. При несимметричном КЗ фазные напряжения будут несимметричные, а значит их можно разложить на симметричные составляющие.

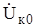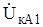Протекание токов обратной и нулевой последовательностей условно можно рассматривать как результат возникновения в месте КЗ напряжений соответствующих последовательностей. При протекании тока по цепи от места КЗ к источнику питания напряжения нулевой и обратной последовательностей уменьшаются соответственно от и до нуля, а напряжение прямой последовательности возрастает от до 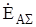(см. рис. 8.3).

Система уравнений (8.13) содержит шесть неизвестных величин: три составляющие напряжения и три составляющие тока. Недостающие для определения этих величин три уравнения будут получены из, так называемых, граничных условий, которыми характеризуется определенный вид КЗ.

Задача нахождения токов и напряжений при заданном несимметричном КЗ сводится к вычислению симметричных составляющих этих величин для фазы А. После того как последние будут найдены, фазные величины токов и напряжений вычисляются либо по выражениям (8.2), (8.3), (8.4), либо (8.6).

Таким образом, для расчета несимметричных токов и напряжений необходимо составлять схемы замещения прямой, обратной и нулевой последовательностей с соответствующими сопротивлениями отдельных элементов.