Уравнение равновесия моментов

Кроме электромагнитного вращающего момента М, развиваемого якорем двигателя, к его валу могут быть приложены момент холостого хода М_о, полезный момент М₂ на валу двигателя и динамический момент М_дин.

Момент холостого хода М_оопределяется потерями на трение в подшипниках, якоря о воздух, щеток о коллектор, венти­ляционными потерями и потерями в стали.

Полезный момент М₂ - это противодействующий мо­мент рабочей машины, приводимой в действие данным двигателем; этот момент зависит от нагрузки машины.

Динамический момент возникает при всяком измене­нии скорости вращения вала двигателя и определяется формулой

,

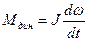где J - момент инерции вращающихся частей двигателя и рабочей машины; ω - угловая скорость вращения.

Если скорость двигателя повышается, то динамический момент увеличивает тормозной момент на валу двигателя, а если она умень­шается, например при остановке двигателя, то динамический момент уменьшает общий тормозной момент двигателя,

Согласно уравнению равновесия моментов, вращающий и тор­мозной моменты в любых условиях работы двигателя находятся во взаимном равновесии, т. е. равны друг другу по величине, но направлены в противоположные стороны:

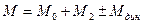
При установившемся режиме работы скорость вращения двига­теля постоянна, а динамический момент равен нулю. Если сумму моментов М_о + М₂ назвать статическим моментом сопротивления на валу двигателя М_ст то

.

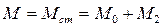В установившемся режиме работы вращающий момент двигателя и статический момент сопротивления на его валу находятся во взаим­ном равновесии.

Мощность, развиваемую якорем, называют электромагнитной:

.

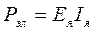Из механики известно, что эта же мощность может быть выражена произведением вращающего момента на угловую скорость:

Р_э = Мω

Тогда Е_Я1_Я = Мω. Отсюда

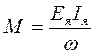
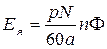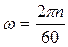Но так как , а , то

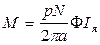, Н м.

Так как выражение 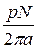для данной машины величина постоянная, то его можно обозначить как коэффициент С_м. Тогда

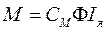Н м.

На практике применяют следующую формулу момента:

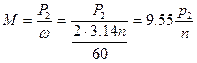Н м,

где Р₂ – мощность двигателя на валу, Вт; n – скорость вращения вала, об/мин.