Электрическая цепь с параллельным соединением ветвей

Будем считать заданными проводимость резистивного элемента g =1/r и комплексные проводимости индуктивного и емкостного элементов:

.

Кроме того, задана величина 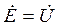, равная напряжению, приложенному к каждому из элементов схемы.

По первому закону Кирхгофа можно записать:

.

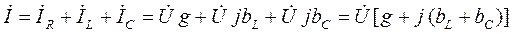Сумма комплексных проводимостей всех параллельных ветвей равна комплексной проводимости данной цепи:

.

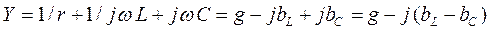Обратная величина комплексной проводимости - это комплексное сопротивление:

.

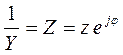Поэтому в показательной форме комплексная проводимость Y равна:

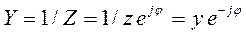
и в тригонометрической форме:

,

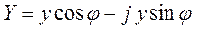где 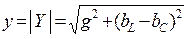– модуль комплексной проводимости цепи, или полная проводимость цепи,

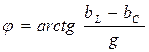– аргумент комплексной проводимости цепи.

На комплексной плоскости слагаемые комплексной проводимости могут быть изображены в виде векторов для двух случаев: b_L > b_C и b_L < b_C. В первом случае комплексная проводимость цепи имеет индуктивный характер, во втором - емкостной.

Комплексное значение тока 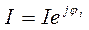можно рассчитать следующим образом:

,

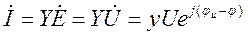а из этого следует, что действующее значение тока в неразветвленной части цепи равно:

.

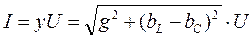Приведем векторные диаграммы напряжения и токов рассматриваемой цепи для двух случаев: b_L > b_C и b_L < b_C:

Если комплексная проводимость цепи имеет индуктивный характер, то общий ток отстает по фазе от напряжения, то есть 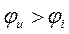, и наоборот, если комплексная проводимость цепи имеет емкостной характер, то общий ток опережает по фазе напряжение, то есть .

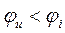Комплексная мощность анализируемой цепи

,

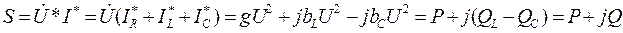где S - полная мощность [В*А], P - активная мощность [Вт], Q - реактивная мощность [вар].