Поведение наполненного и ненаполненного полимера
Композиционный материал (КМ) представляет собой гетерогенную многофазную систему, состоящую из компонентов, которые резко отличаются друг от друга по своим деформационным и прочностным свойствам, поэтому поведение КМ в поле механических сил резко отличается от поведения однородного материала (сталь, бронза).
Если однородное тело оказывается в поле действия механических сил, то в нем возникает напряженное состояние. По мере увеличения внешней нагрузки уровень напряжения в объеме также возрастает. Т.к. тело однородное, то на всем протяжении от места приложения нагрузки и возникновения напряжения до его разрушения будет сохраняться однородное напряженное состояние, т.е. во всех точках величина напряжения будет одинакова.
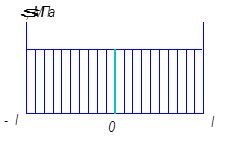
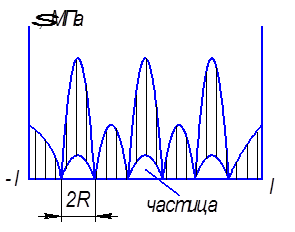
Если в непрерывной поточной среде имеются включения наполнителя, то эпюра распределения напряжений имеет следующий вид:
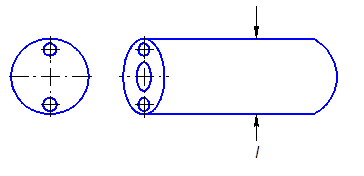
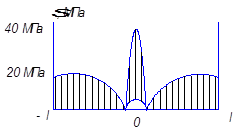
l – толщина образца
R – радиус сферы-наполнителя
На границе раздела фаз будет скачок напряжения, что определяется различными деформационно-прочностными свойствами полимеров.
Наполнитель, обладая более высоким модулем упругости, деформируется меньше, чем матрица, следовательно слой связующего, прилегающего к наполнителю, деформируется меньше. Снижение напряжения происходит по параболе. Т.к. прочность наполнителя больше, чем прочность матрицы, то наполнитель легко выдерживает действующую на него нагрузку. Тогда если модуль упругости наполнителя больше, чем модуль упругости матрицы в 2 раза, то напряжение, развивающееся в наполнителе будет в 2 раза больше, чем в матрице.
Напряжение, возникающее в наполнителе количественно оценивается в различных точках с помощью уравнения:
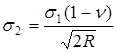 , где
, где
n ‑ коэффициент Пуассона, характеризующий отношение поперечной деформации к продольной
R – радиус частицы
σ1 – напряжение в матрице
σ2 – напряжение, возникающее в наполнителе
Уменьшение напряжения в объеме композита определяется деформационными свойствами наполнителя, в частности – его модулем упругости. Чем больше модуль упругости наполнителя, тем меньше напряжение испытывает армированная матрица.
Величина напряжения в неармированной матрице в соответствии с законом Гука пропорционально модулю матрицы:
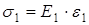 , где
, где 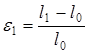 ,
,
l0 – начальная длина
l1 – конечная длина при приложении напряжения
Если при введении частиц наполнителя деформация матрицы будет определяться действующим напряжением, которое будет как у ненаполненных пластиков, то деформация наполнителя будет определяться:
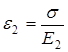
Т.к. жесткий наполнитель не дает матрице растягиваться, то ε1 = ε2.
Отсюда в наполненном композите: 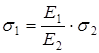
Т.е. действующее напряжение обратно пропорционально модулю упругости наполнителя.
Обычно в качестве наполнителя применяют вещества, у которых модули упругости в 10000 раз больше, чем у матрицы.
Большое значение для прочностных свойств КМ оказывает не только величина модуля упругости, но и форма частиц. Она определяет площадь поверхности контакта наполнителя с матрицей.
Сопоставляя круглую частицу с частицей в форме эллипса, можно убедиться, что нагрузка, воспринимаемая частицей вытянутой формы значительно выше, чем сферической.
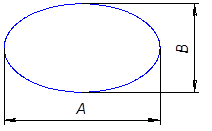
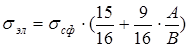
Чем более вытянута А, тем большую часть нагрузки воспринимает вторичная фаза.
Идеальным вариантом наполнителя являются вытянутые сферы вдоль оси тела, диаметр которого меньше длины. Эти наполнители способны полностью воспринимать внешнюю нагрузку. Благодаря высокой поверхности контакта вторичная фаза доминирует, облегчая работу матрицы. Если в матрице имеется несколько частиц, то эпюра напряжения будет иметь следующий вид:
Изменение фронта трещин при встрече с частицей, если материал не армирован и его подвергнуть растяжению, то в нем появится напряжение. Когда оно достигает критической величины, то в нем возникает трещина, которая называется «магистральной». Материал в этом случае разрушается. В наполненном материале, если он подвергнут растяжению, то развивающаяся частица натыкается на частицу наполнителя и огибает ее. Фронт длины трещины увеличивается, а армированная матрица при этом напряжении не разрушается.
2.2. Критическая длина волокна. Эпюры напряжений
Появление в матричной фазе длинных элементов с поперечным размером много меньше длины значительно сказывается на механическом сопротивлении системы. Волокна и полимерная матрица соприкасаются по поверхности наполнителя, который усилие от матрицы. Это усилие трансформируется в усилие волокна.
Чем длиннее волокно, тем больше поверхность контакта и сильнее взаимодействие фаз. Если представить, что внешняя нагрузка стремится увлечь волокно из матрицы, действуя на него, то на границе раздела появляются касательные напряжения. Одновременно напряжение в волокне трансформируется в растяг, т.е. нормальное напряжение.
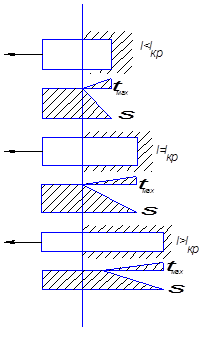
τ ‑ касательные напряжения, развивающиеся в волокне
s ‑ растягивающее (нормальное) напряжение
lкр ‑ критическая длина волокна
Критическая длина – длина, на которой прочностные свойства используются полностью. Если волокно короткое (l < lкр), то напряжения небольшие. При достаточно большой длине волокна (l = lкр) касательные напряжения достигают максимума и при дальнейшем изменении длины волокна не изменяются. Наибольшее касательное напряжение имеет место на самом конце волокна и на длине lкр доходит до нуля. На длинных волокнах, начиная с этой длины, касательные напряжения отсутствуют.
Количественная зависимость между прочностными показателями волокна, его геометрическими характеристиками и напряжениями, возникающими на границе разделов:
1) Нагрузка, вызывающая напряжение сдвига волокна диаметра d и длиной l определяется:
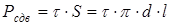 (2.1.)
(2.1.)
2) Усилие сдвига с учетом сохранения статистического равновесия в системе трансформируется в усилие растяжения волокна:
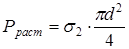 (2.2)
(2.2)
s2 ‑ нормальное растяжение волокна
3) Условие статистического равновесия:
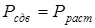 (2.3)
(2.3)
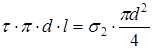 (2.4)
(2.4)
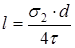 (2.5)
(2.5)
Учитывая, что в полимерной матрице волокно окружено первичной фазой со всех сторон, то длина должна быть в 2 раза больше:
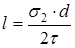 (2.6)
(2.6)
Экспериментально установлено, что τ, которое может выдержать полимерная матрица, составляет некоторую часть от ее прочности:
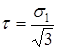 (2.7)
(2.7)
Отсюда (6) идет в (7):
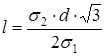 (2.8)
(2.8)
σ2 – нормальное напряжение в волокне, которое растягивает его и может вызвать растрескивание системы. Если σ1 меньше прочности волокна, то растрескивания системы не произойдет.
Адгезионные и химические силы сцепления, как показывает опыт, составляют одну треть от необходимых и реализованных функциональных сил, поэтому для определения критической длины волокна с учетом сил трения и шероховатости используют следующую зависимость:
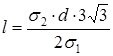 (2.9)
(2.9)
Лекция 5.
Дата добавления: 2021-11-16; просмотров: 527;











