Сопротивление однонаправленного композиционного материала.

Рассмотрим механическое поведение полимерной матрицы, в которой расположены элементарные однонаправленные волокна.

Однонаправленные композиционные материалы имеют площадь поверхности матрицы (рабочей) F₁, у армирующей фазы – F₂.

Относительное удлинение:

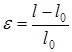_(2.10)

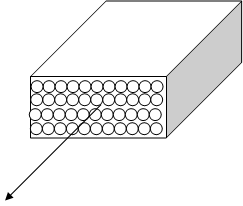
Т.к. при армировании модуль упругости наполнителя намного больше модуля упругости матрицы, т.е. Е₂ > Е₁, то при одноосном растяжении вдоль напряжения армирования деформация композиционного материала будет определяться более жестким наполнителем:

ε₁ = ε₂ = ε (2.11)

Т.о. физическая модель поведения подобного композита будет выглядеть следующим образом:

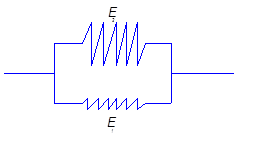
Е₁ – модуль упругости матрицы

Е₂ – модуль упругости наполнителя

В соответствии с законом Гука нагрузка, вызывающая деформацию равна:

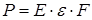(2.12)

Нагрузка складывается из двух составляющих:

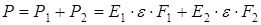(2.13)

Разделим обе части этого уравнения на сумму площадей:

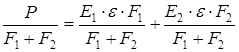(2.14)

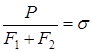
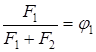
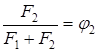
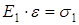
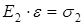
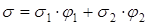(2.16),

где

φ₁ – объемная доля матрицы

φ₂ – объемная доля наполнителя

Если (6) разделить на ε, то получим:

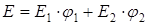(2.17)

Уравнения (6) и (7) – уравнения смеси Фойхта.

Если действие нагрузки на однонаправленный композит перпендикулярно ориентации волокна, то модель механического поведения будет связана с одним напряжением композиционного материала, т.е.:

σ₁ = σ₂ = σ (2.18)

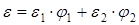(2.19)

Т.к. напряжение σ постоянно, то после деления обеих частей уравнения (9) на σ, получаем:

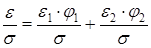(10)

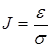‑ податливость системы

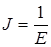
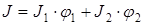(2.19)

Отсюда 1/Е:

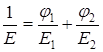(2.20)

Отсюда:

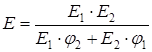– формула Райеса(2.13)

Геометрическая интерпретация однонаправленного композиционного материала механического поведения и смесевых композиционных материалов могут быть аппроксимированы линейной и нелинейной зависимостями.