Общая оценка риска проекта
Таблица 10.3.14.
| Риски, Si | Удельные веса, Wj | Вероят- ность, Pj | Балл, Wi ּ Pi | ||||
| S1 | 0,133 | 10,91 | |||||
| S2 | 0,133 | 10,64 | |||||
| S3 | 0,133 | 9,98 | |||||
| S4 | 0,133 | 9,04 | |||||
| S5 | 0,067 | 3,15 | |||||
| S6 | 0,067 | 2,55 | |||||
| S7 | 0,067 | 2,35 | |||||
| S8 | 0,067 | 2,14 | |||||
| S9 | 0,067 | 2,01 | |||||
| S10 | 0,033 | 0,49 | |||||
| S11 | 0,033 | 0,40 | |||||
| S12 | 0,033 | 0,26 | |||||
| S13 | 0,033 | 0,23 | |||||
| Итого: | 1,0 | X | 54,15 | ||||
Общая оценка риска проекта 54,15 балла, что свидетельствует о средней рискованности рассматриваемого проекта.
Количественная оценка риска проекта в целом может быть выполнена с помощью статистических методов.
СТАТИСТИЧЕСКИЕ МЕТОДЫ ИЗМЕРЕНИЯ ИНВЕСТИЦИОННЫХ РИСКОВ
Расчет среднеквадратического отклонения.
Смысл метода заключается в оценке степени отклонения потока денежных средств для данного инвестиционного проекта от ожидаемого. Чем больше отклонение, тем более рискованным считается проект.
Пример 10.4.Допустим, мы рассматриваем два инвестиционных проекта I и II, по которым оценены возможные денежные потоки при разных состояниях экономики (табл. 10.4.1.).
Таблица 10.4. 1.
Денежные потоки инвестиционных проектов
| Состояние экономики | Денежные потоки, д.е. | |||||||
| I | Вероятность | II | Вероятность | |||||
| Глубокий спад | 0,1 | 0,1 | ||||||
| Средний спад | 0,2 | 0,2 | ||||||
| Нормальное | 0,4 | 0,4 | ||||||
| Небольшой подъем | 0,2 | 0,2 | ||||||
| Рост | 0,1 | 0,1 | ||||||
| Ожидаемое значение | ||||||||
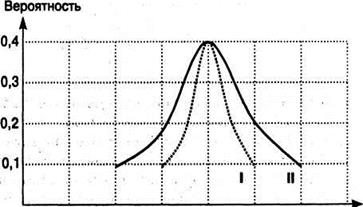
Доход, д.е.
Рис. 10.1.График дисперсии для результатов с неодинаковой вероятностью
Таким образом, из рис. 10.1. видно, что отклонение величины денежного потока от наиболее вероятного значения больше по варианту II, т.е. для него больше и риск. Математически это отклонение (разброс, дисперсия) оценивается средним квадратическим отклонением.
Проекты I и II (рис. 10.2) характеризуются примерно одинаковым среднеквадратическйм отклонением, т.е. Степень риска у них одинаковая, но величина ожидаемого дохода у проекта II выше (Дож2 > Дож1). значит, он эффективнее.
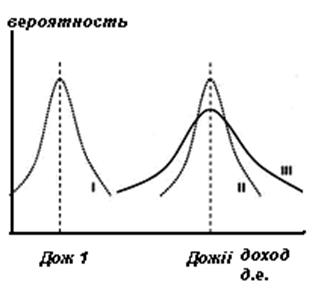
Рис. 10.2.График дисперсии для различных проектов
Проекты II и III характеризуются одинаковой величиной ожидаемого дохода. Однако вероятность его получения у проекта III ниже, кроме того, он и более рискован, так как величина отклонения от ожидаемого дохода у него выше. Поэтому следует выбрать проект II как менее рискованный, но приводящий к такому же ожидаемому результату, что и проект III.
Среднеквадратическое отклонение(δ) является наиболее распространенным показателем оценки уровня инвестиционных рисков. Расчет этого показателя позволяет учесть возможные колебания ожидаемого показателя.
Последовательность расчетов такова.
1. Расчет среднего ожидаемого значения показателя.
Среднее ожидаемое значение — то значение показателя, которое связано с неопределенной ситуацией. Оно является средневзвешенным всех возможных результатов реализации инвестиционного проекта, где вероятность каждого результата используется в качестве веса соответствующего значения, т.е. это как бы средневзвешенное значение всех возможных результатов:
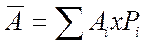
2. Расчет показателя вариации (разброса). Этот показатель измеряет дисперсию (разбросанность) значений [ возможных вариантов реализации инвестиционного проекта вок-4 величины ожидаемого результата. Чем больше вариация, тем боль-; дисперсия (разбросанность) по сравнению с ожидаемым результатом, тем больше риск проекта:
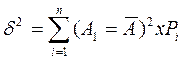
3. Расчет среднего квадратического отклонения (стандартной девиации):
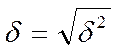
Среднее квадратическое отклонение показывает, на сколько в среднем в абсолютном выражении каждый возможный вариант реализации инвестиционного проекта отклоняется от средней величины. Этот показатель характеризует абсолютную величину риска. Чем выше среднее квадратическое отклонение а, тем выше риск.
Пример 10.5.Сравнить два инвестиционных проекта по уровню риска на основе расчета среднеквадратического отклонения. Основные параметры возможных вариантов реализации проектов приведены в табл. 10.4.2. и 10.4.3.
Таблица 10.4.2.
Распределение вероятностей ожидаемых доходов по вариантам сравниваемых инвестиционных проектов
| Характеристика возможной ситуации | Проект I | Проект II | ||||||
| Расчетный доход, д.е. | Вероятность | Расчетный доход, д.е. | Вероятность | |||||
| оптимистическая | 0,15 | 0,20 | ||||||
| наиболее вероятная | 0,60 | 0,50 | ||||||
| пессимистическая | 0,25 | 0,30 | ||||||
Решение:
Таблица 10.4.3.
Расчет среднего квадратического отклонения
| Характеристика ситуации | Вероятность | Средний ожидаемый доход, д.е. | Показатель вариации, д.е. | |||||
| расчетный доходА | АixPi | AI- 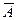
| 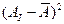
| 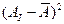 PI PI
| ||||
| ПРОЕКТ 1 | ||||||||
| Оптимистическая | 0,15 | 38,4 | ||||||
| Наиболее вероятная | 0,60 | 21,6 | ||||||
| Пессимистическая | 0,25 | -24 | ||||||
| В целом А =64 |  б2=204
б=14,2 б2=204
б=14,2
| |||||||
| ПРОЕКТ II | ||||||||
| Оптимистическая | 0,20 | 369,8 | ||||||
| Наиболее вероятная | 0,50 | 264,5 | ||||||
| Пессимистическая | 0,30 | -67 | 1346,7 | |||||
В целом А =77  б2= 1981
б=44 б2= 1981
б=44
| ||||||||
Так как б„ = 44 > б, = 14,2 проект II характеризуется большим уровнем риска.
Дата добавления: 2021-11-16; просмотров: 616;











