Понятие множества. Способы задания. Виды множеств. Примеры

Понятие множества. Способы задания. Виды множеств. Примеры

Понятие множества. Способы задания. Виды множеств. Примеры

Под множеством понимают совокупность объектов, «собранных» вместе по какому-то принципу. Основным вопросом здесь является не природа этих объектов (называемых элементами или точками), а их принадлежность или непринадлежность данному множеству. Порядок следования элементов также не важен.

Если а есть один из объектов множества А, мы говорим, что а есть элемент А, или а принадлежит А, а если не принадлежит – то a – не является элементом множества А.

Замечание 2.1(1). То, что объекты, образующие множество, называются точками ничего не говорит об их истинной природе. Точками будут как точки числового множества расположенные на числовой прямой между, скажем, числами 2 и 4, так и неповторимые яркие индивидуальности, составляющие множество студентов 1 курса ВЕИП отделения дистанционного обучения.

Обозначения: Множества обозначают, как правило, заглавными латинскими буквами, элементы (точки) множества – строчными латинскими буквами. 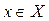означает, что элемент (точка) x принадлежит множеству X, 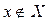, соответственно, не принадлежит (иногда непринадлежность обозначают чертой над знаком принадлежности ).

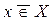Если мы хотим описать множество, мы делаем это, открыв фигурные скобки. Например, X={множество студентов 1 курса ВЕИП отделение дистанционного обучения}.

Способы задания множества:

1) Простым перечислением элементов

A={красный, желтый, зеленый}, описывающее цвета огней светофора

Очевидно, что перечисление элементов удобно

только в том случае, когда множество элементов мало или произвольный элемент характеризуется свойством, которое легко описать.

2)Заданием вида элемента

Часто при перечислении множества используется

описание характеристического свойства элементов этого множества. Например, С = {1³,2³,3³,..., n³,...} описывает множество кубов всех натуральных чисел, а S = {1²,2²,3²,... ,n²} описывает множество квадратов всех положительных чисел, которые меньше или равны n.

3) Заданием некоего общего характеристического свойства элементов множества R={множество действительных чисел} (более подробно об определении множества действительных чисел см п.4.1)

Другой пример: А = {x| x – четное число}. Знак | (или : заменяет обороты «такой что», «такие что», «обладающий свойствами»)

В общем случае множество задается именно путем указания характеристического свойства, т.е. свойства, которому удовлетворяют элементы данного множества, и только они. Для задания обычно используются фигурные скобки, а внутри них приводится характеристическое свойство, описывающее множество. Таким образом, множество {х : х обладает свойством Р} предполагается содержащим только те объекты, которые имеют свойство Р. Например, {х : х — футболист, играющий за РФ} — множество, состоящее из всех футбольных игроков, защищающих честь России на разнообразных турнирах. Запись {х : х —- гражданин России} описывает множество всех граждан России. Способ задания множества должен быть адекватным, т.е. должен полностью определять множество. Это не представляет труда, если объекты множества перечислены. Рассмотрим, однако, множество А = {х : х — высокий студент данного курса} или В = {х : х — хороший студент данного курса}. Если различным студентам курса предложить определить множества A и В, они могут сделать это неоднозначно, выбирая в качестве элементов как множества А, так и множества В не одних и тех же людей. При рассмотрении множества С = {х : х — привлекательная (или красивая) студентка группы} выбрать элементы множества С не только трудно, но не стоит даже пытаться это сделать. Однако, если множество А = {х : х — студент данной группы, рост которого выше 180см} и В = {х : х — студент данной группы, средний балл которого не ниже 4}, то можно сказать определенно, является ли данный студент элементом А или В, так что А и В действительно есть множества.

Множество может вообще не содержать никаких элементов. Тогда оно называется пустым множеством и обозначается Ø. Например, множество клетчатых крокодилов пусто, поскольку вы не найдете ни одного крокодила, который был бы клетчатым.

Множество может состоять только из одного элемента. Такое множество называется одноточечным (одноэлементным). X = {x}. Например, множество президентов Российской Федерации представлено ровно одним человеком.

Множество может содержать конечное число элементов, например, множество студентов вашего курса. Такое множество называется конечным.

Кроме того, множество может содержать бесконечное число элементов – бесконечное множество. В свою очередь бесконечное множество может быть счетным, то есть его элементы можно занумеровать в (бесконечную) последовательность. Примером может служить, скажем, множество натуральных чисел (каждое число задает и свой номер). А также оно может быть несчетным, таково, например, множество действительных чисел (о числе элементов множества подробнее см. тему 6.2.)

Замечание 2.1(2)

Множество нельзя задавать совсем уж произвольно. Рассмотрим известный исторический пример – «парадокс брадобрея». В некотором городе брадобрей бреет всех тех, кто не бреется сам. Принадлежит ли сам брадобрей множеству тех, кого он бреет?

Есть два основных направления «борьбы» с такого рода ситуациями:

- «наивная теория множеств» Г.Кантора, в которой запрещаются все действия и операции, ведущие к парадоксам.

- аксиоматический, при котором множество есть нечто, удовлетворяющее набору аксиом (системы Цермело-Френкеля, Гёделя-Бернайса)