Определение 2.2.(3)

Множества равны, если они содержат одни и те же элементы, порядок элементов, как уже отмечалось, роли не играет.

Иначе говоря,

A=B , если для любого x выполняется: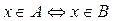

Например, если А ={2,4,6}, а В = {х : х есть четное положительное целое число, которое меньше 7}, тогда А и В — равные множества.

Как уже упоминалось, если не оговаривается обратное, порядок следования элементов в множестве не имеет значения, как и наличие повтора элементов (то есть множество однозначно определяется только элементами, которые оно содержит) , поэтому A={1,2,3,4,5}, B={2,3,1,4,5}, C={1,1,2,3,3,3,5,4,4,4,4}, A = B = C.

Можно определить равенство множеств и следующим образом:

A=B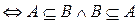

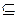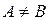Если A B и то говорят, что A - собственное подмножество множества B.

Таким образом, доказательство равенства множеств А и В состоит из двух

этапов:

1) Доказать, что А есть подмножество В.

2) Доказать, что В есть подмножество А.

Замечание 2.2.(2). Рассматривая множества и действия над ними, обычно имеют в виду существование некоторого основного (базового, универсального) множества, из которого черпают примеры множеств. Мы будем обозначать его Ω (это обозначение принято в теории вероятностей, к изучению которой мы перейдем во втором семестре). В теории множеств его обозначают какой-либо заглавной латинской буквой, например М или U.

В некотором смысле основное множество Ω и пустое множество Ø представляют собой противоположности, поскольку пустое множество не содержит элементов, а универсальное множество содержит "все" элементы.

2.2.Операции над множествами. Формула двойственности

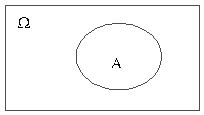Рис.2.2.(1)

Множества удобно изображать в виде рисунка, который называется кругами Эйлера (в теории множеств) или диаграммами Венна(Вьенна) (в логике). На рисунке 2.2.(1) основное множество (пространство)W изображено в виде прямоугольника, а произвольное множество A, заключено в эллипс. Сами элементы (точки) на кругах Эйлера не изображаются, а информация о соотношении между их множествами содержится в расположении границ соответствующих областей.

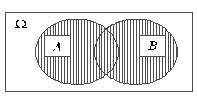
Суммой (объединением)двух множествАиB(обозначается AUB или А+В) называется множество, состоящее из всех элементов, принадлежащих по крайней мере одному из множеств А или B, возможно и обоим, но по крайней мере одному – точно.

 

Рис.2.2.(2)

Приведем пример объединения множеств. Пусть множество А - множество россиян, а множество B – множество студентов, тогда AUB есть множество всех людей, являющихся либо гражданами РФ, либо студентами (возможно, и то и другое, но хотя бы одно условие должно быть выполнено)

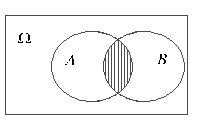
Рис.2.2.(3)

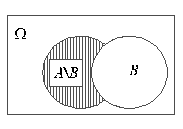
Произведением (пересечением) A∩B (или АВ, А×В )множеств А и B называется множество, состоящее из всех тех точек, которые принадлежат и А и B. В нашем примере это множество учащихся в высших учебных заведениях россиян

 

 

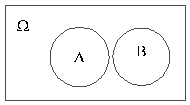Если у множеств нет общих точек (см рис.2.2.(4)), их

Рис. 2.2.(4) их пресечение пусто A∩ B = Ø

 

 

Разностью А\B или А-B событий А и B называется событие, состоящее из всех исходов события А, не благоприятствующих событию B. Диаграмма Венна разности событий А и Bизображена на рисунке 2.2.(5).

Рис.2.2.(5)

В условиях рассмотренного выше примера множествоА\B состоит из тех россиян, которые в данный момент студентами не являются

 

Симметрической разностью А∆В называется событие, состоящее из всех исходов, входящих в события А и В по-отдельности, но не принадлежащие им обоим (на рис. 2.2.(3)) – незаштрихованная область внутри А и В). А∆В = AUB \ A∩B. Это, соответственно, россияне – не студенты и студенты – не россияне.

 

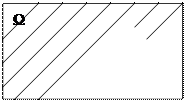
Множество 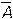= W \ A = С_ΩА, состоящее из всех точек , не принадлежащих множеству А (но принадлежащих определенному основному множеству Ω) дополнением множестваА (до множества (пространства) Ω). (заштрихованная область вне множества А на рис. 2.2.(6)).

 

 

 

Рис. 2.2.(6)

 

 

Замечание. Существенно, что мы находимся все время в рамках одного и того же основного множества – Ω, поскольку без него операцию дополнения просто не определить.

Пример 2.2.(1)

А={1,2,3,4,5,6}

B={0,2,4,6,8,10}

C={9,10}

Ω={0,1,2,3,4,5,6,7,8,9,10}

AUB = {0,1,2,3,4,5,6,8,10}

A∩B = {2,4,6}

A∩C = Ø

А\ B = {1,3,5}

А∆В = {0,1,3,5,8,10}

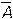= {0,7,8,9,10}

Примеры 2.2.(2)

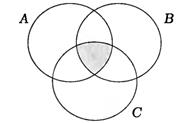закрашенная область – множество A ∩B ∩C

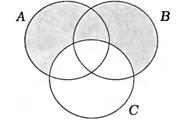закрашенная область – множество (AUB)\ C

Непосредственно из введенных определений следуют равенства: AU 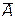=W; A∩ 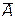=Æ; 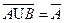∩ 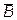; 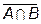= 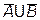. Два последних равенства называются формулами Де Моргана.

Теорема 2.2. Первая формула Де Моргана (Первая формула двойственности)

∩

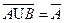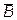
Доказательство

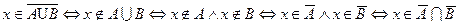
Аналогичное доказательство второй формулы Де Моргана оставим в качестве упражнения.

Системы множеств