Кинетика периодической адсорбции.

Периодическая адсорбция является нестационарным процессом массообмена между потоком разделяемой газовой смеси и неподвижным слоем адсорбента. В общем случае этот процесс характеризуется последовательным массопереносом адсорбтива из ядра потока к поверхности частиц адсорбента (внешний массоперенос) и от этой поверхности - внутрь частиц (внутренний массоперенос). В отдельных случаях процесс может лимитироваться либо внешним, либо внутренним массопереносом.

Расчет адсорберов периодического действия основывают на закономерности изменения во времени степени насыщения адсорбента и концентрации адсорбтива в газовой фазе в каждом сечении слоя адсорбента. Это пространственно - временное распределение поглощаемого компонента между фазами можно представить следующим образом. При входе газового потока с постоянной начальной концентрацией адсорбтива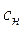(кг/м3) в слой свежего адсорбента с концентрацией поглощаемого компонента (адсорбата) с_т=0адсорбируемый компонент начинает поглощаться первым рядом гранул адсорбента, затем вторым, третьим и т.д. С течением времени вовлекается в работу много последовательно расположенных рядов частиц адсорбента, однако, каждый последующий ряд омывается потоком газа с концентрацией адсорбтива 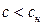, так как часть его уже поглощена предыдущими рядами.

После предельного насыщения частицы первого ряда выключаются из процесса поглощения, и газ с концентрацией 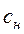начинает омывать частицы второго ряда, затем третьего и т.д. Таким образом, с течением времени по высоте слоя адсорбента Н образуются три зоны (рис.6.3): 1 - зона отработанного адсорбента (высота Н₁), где достигнута предельная емкость (концентрация) 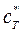(т.е. находящаяся в равновесии с газовым потоком концентрации 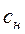); 2 - работающая зона (высота Н₂), где предельная емкость еще не достигнута, и процесс адсорбции продолжается; 3 - зона не включенного еще в работу адсорбента (высота Н₃).

Насыщение первого ряда частиц адсорбента происходит с падающей скоростью, так как по мере приближения к предельному значению 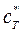непрерывно уменьшается движущая сила процесса.

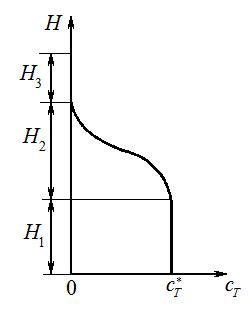
Рис.6.3. Кривая распределения концентрации адсорбата по высоте

слоя адсорбента.

Кинетика адсорбции описываются уравнениями материального баланса, кинетики и изотермы. Запишем уравнение материального баланса без учета коэффициента продольного перемешивания:

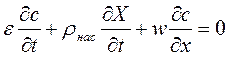(6.11)

Величины с и Х взаимосвязаны. Если процесс протекает при условиях близких к равновесным (равновесная адсорбция), то их связь представляет собой изотерму адсорбции. Решение уравнения (6.11) с учетом вида изотермы (6.10) позволяет найти 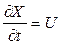, которая является скоростью перемещения по слою точки, имеющий концентрацию с:

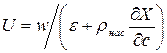(6.12)

где 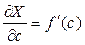- производная функции изотермы в точке с концентрацией с.

Полученное соотношение (6.12) позволяет проанализировать изменение профиля концентрации при его перемещение по слою, т.е. соотношение (6.12) позволяет определить движение фронта сорбции по слою адсорбента.

Необходимо отметить, что скорость движения фронта сорбции всегда меньше средней скорости движения сплошной (подвижной) фазы. На рис.6.4. представлены кривые движения фронта сорбции для различных изотерм.

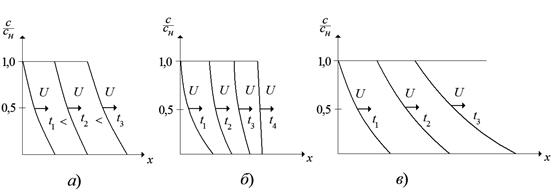
Рис.6.4. Движение фронта сорбции по слою адсорбента при линейной изотерме адсорбции (а); при выпуклой изотерме адсорбции (б); при вогнутой изотерме адсорбции (в).

При линейной изотерме все точки поля концентрации перемещаются с одинаковой скоростью. В случае выпуклой изотерме точки с большей концентрацией будет перемещаться по слою с большей скоростью. В результате этого происходит выравнивание поля концентраций. При вогнутой изотерме адсорбции, наоборот, точки поля концентрации, отвечающие малым значениям концентраций, движутся быстрее точек, соответствующих большим значениям концентраций и поле концентраций вытягивается.

Расчет распределения концентраций в слое адсорбента с учетом продольного перемешивания представляет большие трудности. Известно, что продольное перемешивание обуславливает растяжение поля концентраций в работающем слое адсорбента.