Основное уравнение центробежных машин (уравнение Эйлера)

Основное уравнение определяет напор, создаваемый машиной.

В настоящее время существует две теории, с помощью которых получают основное уравнение центробежных машин – вихревая
и струйная теории.

Рассмотрим струйную теорию Эйлера.

При протекании жидкости через канал между лопатками колеса каждая частица жидкости участвует в двух основных движениях: относительном – вдоль линии канала со скоростью w и переносном
с окружной скоростью 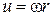, где w – угловая скорость вращения колеса,
r – радиус окружности, на которой находится в данный момент частица жидкости.

Абсолютная скорость c частицы складывается геометрически
из скоростей переносного и относительного движений:

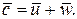(6.19)

В данном случае скорости переносного движения различны
для различных точек.

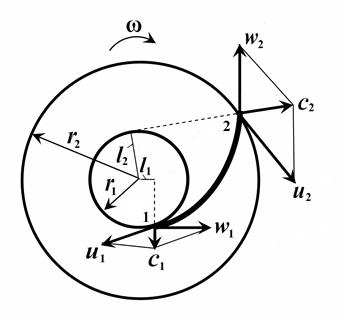
Будем считать, что траектория частицы жидкости совпадает
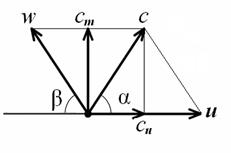
с очертанием профиля лопатки. Такую картину наблюдали бы, если бы число лопаток было бесконечно велико, а их толщина была бесконечно малой. Это означает, что относительная скорость 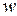является касательной во всех точках к профилю лопатки. Переносная скорость u направлена
по касательной к окружности.

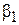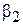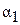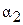Индексами 1 обозначим величины, относящиеся к входному сечению, а индексами 2 – к выходному. Углы и (между касательной к окружности и касательной к лопатке) называются углами входа и выхода лопаток, углы и (между касательной к окружности и абсолютной скоростью) – углами входа и выхода жидкости (рис. 6.6).

Рис. 6.6. Картина скоростей рабочего колеса центробежного насоса

Для вывода основного уравнения центробежных машин воспользуемся теоремой о моменте количества движения. Для нашего случая она может быть сформулирована следующим образом: изменение
в единицу времени момента количества движения относительно оси колеса равна крутящему моменту на валу машины.

Крутящий момент на валу машины определяется как:

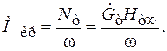(6.20)

Здесь – мощность на валу машины, w – угловая скорость вращения вала, 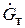– весовая подача машины, 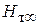– теоретический напор машины при бесконечном числе лопаток.

Момент количества движения жидкости в единицу времени

на входе жидкости в рабочее колесо:

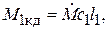
на выходе:

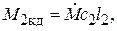
изменение:

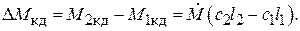(6.21)

Здесь 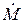– массовая подача жидкости.

В выражении (6.21) неизвестные величины 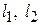заменим через известные. С этой целью общую скорость 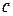разложим на две составляющие:

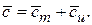(6.22)

Здесь 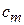– меридианальная (радиальная) скорость, проходящая через центр рабочего колеса и момента не дает; 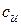– проекция абсолютной скорости на направление переносной скорости u, для которой плечо r. С учетом этого перепишем уравнение (6.21):

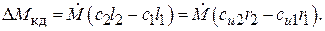(6.23)

По теореме о количестве движения:

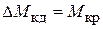или 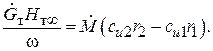(6.24)

Решая зависимость относительно 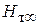, получим:

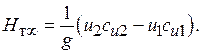(6.25)

Это и есть основное уравнение центробежных машин – уравнение Эйлера. Оно было получено Эйлером в 1754 году, а центробежный насос был изобретен в 1835 году.

С целью достижения максимального значения 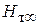рабочие колеса обычно выполняют так, что жидкость входит на лопатку почти радиально. В этом случае a₁ = 90 ° и 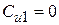. Тогда получим:

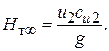(6.26)

Действительный напор H, создаваемый насосом, меньше теоретического по двум причинам:

– часть напора затрачивается на преодоление гидравлических сопротивлений внутри насоса;

– не все частицы жидкости в канале между двумя лопатками движутся по одинаковым траекториям, вследствие этого возникает циркуляция жидкости в канале.

Первое учитывается гидравлическим КПД 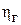, второй – коэффициентом конечного числа лопаток .

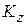В результате для действительного напора 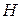получим выражение:

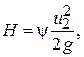(6.27)

где 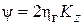f – коэффициент напора, f – коэффициент закручивания потока f = .

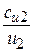Для насосов со спиралеобразным отводом жидкости из рабочего колеса 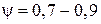, для насосов турбинного типа (с направляющим аппаратом в корпусе насоса) .

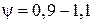По формуле (6.27) определяется, обычно, ориентировочное значение напора центробежного насоса.