Образование и движение капель и газовых пузырей. Барботаж

Диспергирование жидкости и газа в целях увеличения межфазной поверхности широко применяется в промышленной технологии (абсорбция, ректификация, экстракция и т.д.). Во всех случаях необходимо знать размеры, частоту образования и закономерности движения капель и пузырей.

Диспергирование капельных жидкостей в газовой среде. Возможны два режима диспергирования при истечении жидкости
из отверстия: капельный и струйный. В первом случае капля образуется непосредственно при истечении жидкости из отверстия. Во втором случае из отверстия вытекает струя, распадающаяся в дальнейшем
на полидисперсные капли.

Рассмотрим капельный режим истечения жидкости в газовой среде(рис. 3.10). Этот режим реализуется при небольших скоростях подачи жидкости w.

Определим диаметр капли 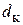в момент отрыва от сопла. Будем считать каплю сферической. Вблизи отверстия перед отрывом капли образуется более тонкая шейка .

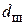а) б)

Рис. 3.10. Диспергирование:

а – образование капли; б – образование пузыря

Отрыв капли наступает в момент равенства следующих сил (вариант а):

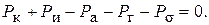(3.64)

Здесь 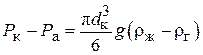– соответственно вес капли
и выталкивающая архимедова сила;

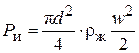– сила инерции потока жидкости;

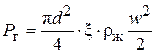– сила сопротивления при выходе жидкости
из сопла;

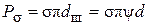– сила поверхностного натяжения.

Коэффициент местного сопротивления x при выходе жидкости
в газ 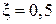, коэффициент сужения .

Из уравнения (3.64) для диаметра капли 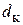получена следующая формула:

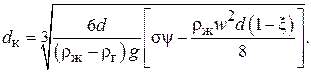(3.65)

В случае очень низких скоростей подвода жидкости w инерционной силой и силой сопротивления выхода жидкости из сопла можно пренебречь. Тогда формула (3.65) упрощается и принимает вид:

(3.66)

Зависимость (3.66) получена в предположении равенства
сил тяжести капли и подъемной архимедовой силы с силами поверхностного натяжения.

Однако зависимость (3.64) справедлива только к началу отрыва капли от сопла. Отрыв же происходит не мгновенно, а в течение некоторого времени с образованием шейки переменных размеров.

В начальный момент отрыва скорость капли меньше средней скорости истечения жидкости из сопла. В это время происходит втекание некоторой массы жидкости в каплю. Вследствие прироста массы капли её равновесие нарушается. Капля получает ускорение, её скорость становится равной и большей скорости питающей её струи, и, как следствие, происходит разрыв шейки капли.

Учет динамики процесса образования капли может дать в некоторых случаях до 30 % прибавки массы капли. Динамическая теория каплеобразования разработана и экспериментально исследована на кафедре гидравлики КГТУ (КХТИ) (Зиннатуллин Н. Х., Нафиков И. М.).

Определим частоту образования капель , исходя из объемного расхода диспергируемой фазы 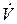и объема капель :

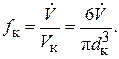(3.67)

Увеличение расхода жидкости через сопло приводит к смене режима истечения – капельное истечение переходит в струйное. Струя
в дальнейшем под действием возмущений распадается на полидисперсные капли. Следовательно, увеличение расхода жидкости приводит к потере технологического процесса. Общепринятой теории смены режимов
при истечении жидкостей из сопла не существует. Как один из вариантов определения смены режимов может быть предложено использование критериев Вебера 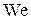и Бонда (рис. 3.11).

Здесь ,

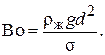
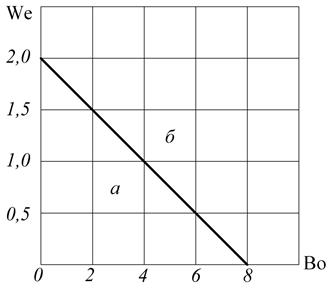
Рис. 3.11. Зависимость :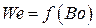

а – зона устойчивого каплеобразования;

б – зона устойчивого струеобразования

В промышленности для распыления жидкости в газовом потоке применяются различные механические устройства. Для распыления жидкости используется как кинетическая энергия самой жидкости, так
и кинетическая энергия самого газа. Ниже предлагается классификация механических распылителей:

– струйные форсунки;

– форсунки с соударяющимися струями;

– центробежные форсунки;

– центробежные распылители;

– ультразвуковые форсунки;

– распылители при соосных потоках газа и жидкости;

– распылители при подаче жидкости под углом к потоку газа.

При движении мелких капель в газовой среде можно использовать уравнения, полученные для обтекания твердых частиц. Однако
с увеличением размеров капли ситуация меняется. На жидкой границе раздела фаз касательная составляющая скорости отлична от нуля, вследствие чего внутри движущейся капли возникает циркуляция среды. Циркуляция способствует лучшему обтеканию капли по сравнению
с твердой сферой. Отрыв потока при движении капли наблюдается в более высоких значениях 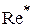. Скорость движения небольших капель при 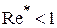может быть определена по следующей формуле:

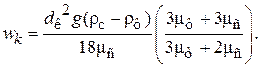(3.68)

Здесь индекс «с» – дисперсионная среда, «ф» – дисперсная фаза.

Увеличение диаметра капель приводит к их деформации
и дальнейшему их разрушению на мелкие капли (рис. 3.12). Траектории
их движения отличаются от вертикальной.

а) б) в)

Рис. 3.12. Движение капли в газовом потоке:

а – сферическая капля; б – деформированная капля;
в – крупная капля в стадии разрушения

Рассмотренные выше положения относятся к движению одиночных капель. При совместном движении капель наблюдается их гидродинамическое взаимодействие. Здесь закономерности движения изменяются, общий эффект аналогичен стесненному осаждению твердых частиц, т.е. движение капель относительно газа замедляется. Одновременно ситуация осложняется постоянной коалесценцией
и разрушением дискретных образований и их деформацией.

Образование газовых пузырей в жидкой среде. Рассмотрим образование газовых пузырей в жидкой среде (рис. 3.10, б). При небольших скоростях подачи газа образуются отдельные пузыри и всплывают наверх. С увеличением скорости происходит быстрое образование пузырей, и они образуют цепочку. Дальнейшее увеличение приведет
к образованию струи газа, которая впоследствии распадается
на отдельные пузыри.

Образование отдельного пузыря может быть описано уравнением (3.64). Однако силы инерции и силы сопротивления потока газа по сравнению остальными членами незначительны, поэтому их отбросим. Архимедова подъемная сила больше веса пузыря, следовательно, пузырь поднимается вверх. Для этого случая получим:

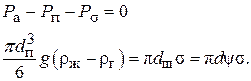
Из последнего уравнения находим :

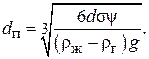(3.69)

Частота образования пузыря определяется по формуле (3.67).

С некоторого критического расхода газа начинается цепное движение пузырей. При расходе газа выше критического диаметр пузырей увеличивается согласно формуле:

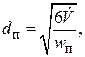(3.70)

где 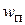– скорость всплывания пузыря.

При установившемся движении одиночного пузыря на него действует подъемная сила 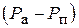и равная ей сила сопротивления жидкости. Это соотношение, как известно, для ламинарного случая всплытия пузыря дает формулу Стокса. Формула Стокса справедлива для очень маленьких пузырей порядка 1,5 мм.

Вследствие подвижности раздела фаз газовый пузырек всплывает с большей скоростью, чем твердая частица такого же размера при прочих равных условиях. Скорость ламинарного всплытия сферического газового пузырька с учётом зависимости (3.68) была получена в виде:

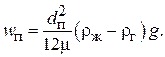(3.71)

С увеличением размера пузыря из-за неравномерности давления
по окружности пузырь всё больше деформируется, отклоняясь
от сферической формы. Для больших пузырей влияние сил поверхностного натяжения становится малым по сравнению с динамическим воздействием жидкой среды, и пузырь приобретает неустойчивую форму (рис. 3.13).

Траектория всплытия больших пузырей отличается от вертикальной. Возможно всплытие таких пузырей по спирали, их дробление
и коалесценция. ПАВ упрочняет межфазную поверхность, и скорость движения пузырей уменьшается, приближаясь к величине, рассчитанной по формуле Стокса.

Рис. 3.13. Формы всплывания пузырей различных размеров:

1 – мм; 2 – 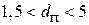мм; 3 – мм; 4 – мм

Барботаж. Прохождение газа в жидкость через множество отверстий называется массовым барботажем. При малых скоростях газа в режиме всплытия отдельных пузырей к ним применимы закономерности, полученные ранее. При расходах газа, превышающих критический , происходит стесненное движение пузырей, и эти закономерности нарушаются. При дальнейшем увеличении расхода газа образуется слой пены. Ещё большее увеличение расхода газа приведет к струйному течению газа через слой жидкости.

Следует отметить, что возникающая при барботаже пена нестабильна и разрушается сразу после прекращения подачи газа.

Пена характеризуется газосодержанием e и удельной поверхностью контакта газа и жидкости a. Под газосодержанием e понимают долю объема газовой фазы в общем объеме пены.

Удельной поверхностью называют поверхность контакта фаз между газом и жидкостью в единице объема пены.

Определим эти величины. Обозначим высоту слоя пены через ,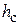
а высоту светлого (чистого) слоя жидкости через , площадь поперечного сечения аппарата – F. Тогда газосодержание e (порозность) можно определить по формуле:

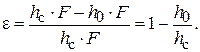(3.72)

Здесь 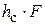– объем пены, 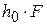– объем жидкости.

Предположим, что в пене находится n пузырей средним диаметром 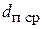. Тогда объем пены можно представить:

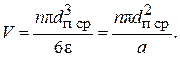
Откуда получим выражение для удельной поверхности a:

(3.73)

Значение 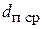можно определить по формуле (3.70), принимая вместо 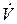его критическое значение .

Пена имеет наибольшую поверхность контакта фаз для газожидкостной системы.