Движение жидкости через неподвижный зернистый слой
При прохождении жидкости через слой зернистого материала
в качестве параметра, характеризующего движение, берется
фиктивнаяскорость 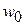 , отнесенная ко всей площади аппарата:
, отнесенная ко всей площади аппарата: 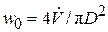 .
.
Наблюдениями установлено, что при малых скоростях движения жидкости 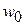 , не превышающих некоторого значения
, не превышающих некоторого значения 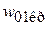 , слой неподвижен, высота слоя и порозность остаются постоянными
, слой неподвижен, высота слоя и порозность остаются постоянными 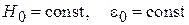 . Жидкость (газ) движется по извилистым каналам, образованным поверхностями частиц (рис. 3.2).
. Жидкость (газ) движется по извилистым каналам, образованным поверхностями частиц (рис. 3.2).
Этот режим называется режимом фильтрации.
Установим границы этого режима. С ростом скорости при достижении некоторого значения 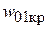 , частицы слегка отодвигаются друг от друга, объем слоя несколько увеличивается. Этот момент характеризуется тем, что сила давления потока на слой сравнима с силой тяжести всех частиц:
, частицы слегка отодвигаются друг от друга, объем слоя несколько увеличивается. Этот момент характеризуется тем, что сила давления потока на слой сравнима с силой тяжести всех частиц:
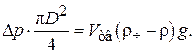 (3.5)
(3.5)
где 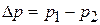 – гидравлическое сопротивление слоя,
– гидравлическое сопротивление слоя, 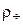 – плотность частица, r – плотность жидкой среды. Скорость
– плотность частица, r – плотность жидкой среды. Скорость 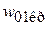 является верхним пределом существования неподвижного зернистого слоя, т.е. режима фильтрации.
является верхним пределом существования неподвижного зернистого слоя, т.е. режима фильтрации.
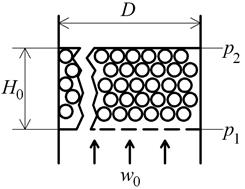
Рис. 3.2. Слой неподвижного зернистого материала
Для нижнего и верхнего живого сечений аппарата давления, соответственно, 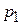 и
и 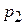 . Они общие для всех капилляров. Если мы определим сопротивление для одного капилляра, то это и будет гидравлическим сопротивлением для всего зернистого слоя. Запишем уравнение Дарси – Вейсбаха для одного капилляра:
. Они общие для всех капилляров. Если мы определим сопротивление для одного капилляра, то это и будет гидравлическим сопротивлением для всего зернистого слоя. Запишем уравнение Дарси – Вейсбаха для одного капилляра:
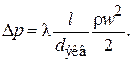 (3.6)
(3.6)
Здесь l – коэффициент сопротивления капилляра, учитывающий все виды потерь (на трение, местные), l – длина капилляра, 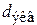 – эквивалентный диаметр капилляра, w – действительная средняя скорость движения жидкости по капилляру.
– эквивалентный диаметр капилляра, w – действительная средняя скорость движения жидкости по капилляру.
Определим неизвестные величины, входящие в (3.6), через известные.
1. Если средняя длина капилляров представляет собой высоту слоя
в 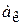 раз, то средняя длина капилляра
раз, то средняя длина капилляра 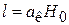 . Коэффициент кривизны капилляра
. Коэффициент кривизны капилляра 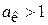 .
.
2. Как известно, 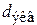 определяется как учетверенное отношение живого сечения потока на смоченный периметр.
определяется как учетверенное отношение живого сечения потока на смоченный периметр.
Для нашего случая свободное сечение слоя составляет 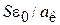 ,
,
а смоченный периметр свободного слоя – 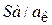 . Итак, для эквивалентного диаметра капилляра получим:
. Итак, для эквивалентного диаметра капилляра получим:
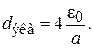 (3.7)
(3.7)
Эквивалентный диаметр может быть выражен также через размер частиц зернистого слоя 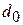 .
.
Пусть в объеме слоя V имеется n частиц. Объем частиц 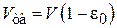 , а их поверхность –
, а их поверхность – 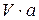 .
.
Средний объем одной частицы:
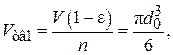 (3.8)
(3.8)
а её поверхность
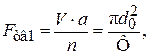 (3.9)
(3.9)
Из соотношений (3.8) и (3.9) найдем а:
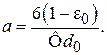 (3.10)
(3.10)
Подставим в (3.7) значение а из (3.10) и найдем:
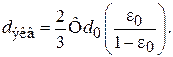 (3.11)
(3.11)
Для нахождения истинной скорости w запишем уравнение неразрывности:
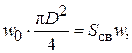 (3.12)
(3.12)
где 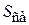 – свободное сечение слоя,
– свободное сечение слоя, 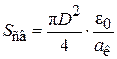 . Принимая
. Принимая 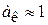 , найдем:
, найдем:
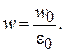 (3.13)
(3.13)
С учетом приведенных зависимостей уравнение (3.6) примет вид:
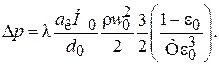 (3.14)
(3.14)
Коэффициент сопротивления l зависит от гидродинамического режима течения жидкости в капилляре, который определяется критерием Рейнольдса:
|
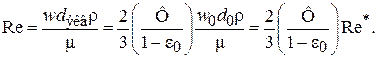 (3.15)
(3.15)
где 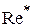 – модифицированный критерий Рейнольдса.
– модифицированный критерий Рейнольдса.
По многочисленным экспериментальным данным для всех режимов течения l можно определить по обобщенной зависимости:
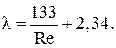 (3.16)
(3.16)
При малых значениях Re вторым членом зависимости (3.15) можно пренебречь (в формуле (3.16) обычное Re).
При 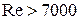 наступает автомодельный турбулентный режим.
наступает автомодельный турбулентный режим.
При этом l не зависит от Re и становится постоянным: 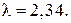
Заметим, как и для всех ламинарных течений 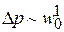 , для турбулентных
, для турбулентных 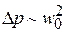 .
.
Значения e0, a, Ф находятся опытным путем и приводятся
в справочной литературе. Так, при свободной засыпке слоя шарообразных частиц 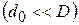 получено
получено 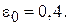
Дата добавления: 2018-05-10; просмотров: 1950;











