Характеристика зернистого слоя

ДИНАМИКА ДВУХФАЗНЫХ ПОТОКОВ

В природе и промышленности довольно часто встречаются гетерогенные многофазные системы. Рассмотрим двухфазную систему,
как наиболее простую. В таких системах различают сплошную фазу, называемую дисперсионной средой, и дисперсную фазу, распределенную
в первой в виде отдельных включений. Как дисперсионная среда, так
и дисперсная фаза могут находиться в трех агрегатных состояниях – твердом, жидком и газообразном.

Системы с подвижной дисперсионной средой подразделяются на системы «жидкость (газ) – твердое тело», «газ (пар) – жидкость», «жидкость – жидкость».

Двухфазные системы обладают высокой поверхностью контакта дисперсной и сплошной фаз, поэтому все контактные процессы (тепло-
и массообменные) протекают с большей интенсивностью.

Описание закономерностей движения двухфазных систем осложняется неоднородностью их состава и различием скорости движения фаз.

Общая задача гидромеханического расчета двухфазных систем состоит в установлении закономерностей переноса импульса при взаимном движении фаз.

Система «жидкость (газ) – твердое тело»

Характеристика зернистого слоя

В промышленной технологии многие процессы протекают
в аппаратах, заполненных зернистым материалом или насадкой. Зернистые материалы обычно имеют разнообразную форму и бывают разного размера. При заполнении жидкостью свободного пространства между частицами слоя зернистого материала поток одновременно обтекает отдельные частицы или элементы слоя и движется внутри пор и пустот, образующих систему извилистых каналов переменного сечения.

Анализ такого движения представляет собой смешанную задачу гидравлики. Однако для упрощения расчетов подобных процессов их относят к внутренней задаче (течение внутри канала).

Определим характеристики зернистого слоя.

Удельная поверхность слоя 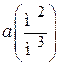представляет собой суммарную поверхность всех частиц, находящихся в единице объема, занятого слоем.

Порозность зернистого слоя e характеризует долю свободного объема между частицами и определяется следующим образом:

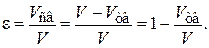(3.1)

Здесь V – полный объем, занимаемый дисперсной системой; 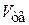– суммарный объем твердых частиц; 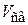– свободный объем между частицами.

В общем случае зернистый слой представляет собой совокупность большого числа частиц различной формы и размеров, точное описание, которого практически невозможно. Поэтому обычно вводятся некоторые осредненные параметры слоя. Так, частицы произвольной формы условно заменяются сферическими частицами.

За размер частицы принимают диаметр шара эквивалентного объема 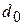или эквивалентной поверхности :

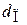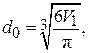
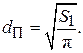(3.2)

Здесь 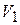и 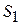– объем и поверхность одной частицы. Для характеристики отклонения формы частицы от сферической вводится Фактор формы Ф:

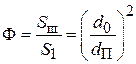. (3.3)

Здесь 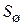– площадь поверхности шара, имеющего тот же объем, что частица с площадью поверхности .

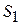Для полидисперсных зернистых слоев средний диаметр частиц определяется по формуле:

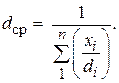(3.4)

Здесь 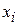– объемная или массовая (при одинаковой плотности частиц) доля частиц с диаметром .

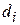Для определения 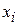производится фракционный анализ.

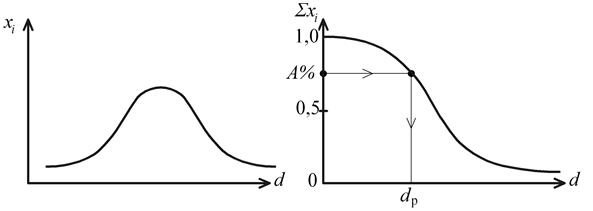
Очень часто распределение частиц по размерам следует нормальному или нормально-логарифмическому закону, что соответствует некоторым моделям. По кривой распределения строится интегральная кривая распределения. По интегральной кривой распределения можно определить расчетный диаметр для данного технологического процесса (рис. 3.1).

а) б)

Рис. 3.1. Фракционная характеристика зернистого слоя:

а – кривая распределения частиц по размерам;

б – интегральная кривая распределения частиц

Предположим, что при расчете пылеосадительной камеры
по экологическим и экономическим соображениям установили, что необходимо уловить А% технологической пыли. Тогда по ординате интегральной кривой распределения отмечаем А% и по кривой находим 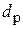. Пылеосадительная камера рассчитывается на 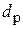. Частицы, имеющие размеры 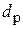и выше, будут уловлены.