Кристаллическая решетка
При описании правильной внутренней структуры кристаллов обычно пользуются понятием кристаллической решетки.
Кристаллическая решетка представляет собой пространственную сетку, в узлах которой располагаются частицы (атомы, ионы или молекулы), образующие кристалл.
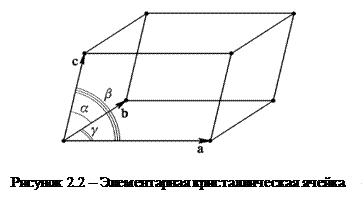
В основе кристаллической решетки лежит элементарная кристаллическая ячейка, представляющая собой параллелепипед минимального объема с характерным для данной решетки расположением атомов (рисунок 2.2). Если взять большое число одинаковых кристаллических ячеек и вплотную уложить их в определенном объеме, сохраняя параллельность ребер и граней, то мы будем иметь пример строения идеального монокристалла.
Формы кристаллов чрезвычайно разнообразны. Изучением их занимается наука кристаллография.
 |
Важнейшим геометрическим свойством кристаллов, кристаллических решеток и их элементарных ячеек является симметрия (т.е. свойство совмещаться с собой) по отношению к определенным направлениям (осям) и плоскостям.
В кристаллах число элементов симметрии ограничено. В них, как в конечных фигурах, различаются следующие элементы симметрии: зеркальная плоскость симметрии, поворотная ось симметрии (простая и винтовая), центр симметрии или центр инверсии.
Зеркальная плоскость симметрии соответствует простому отражению в плоскости, как в зеркале. Такая плоскость делит тело на две равные части, совпадающие друг с другом всеми своими точками при отражении в этой плоскости.
Простая поворотная ось симметрии - прямая линия, при повороте вокруг которой на долю окружности, равную 1/n (где n - порядок оси) фигура совмещается сама с собой всеми своими точками.
Зеркально-поворотные оси сочетают одновременно действие поворота около оси на долю окружности 1/n и отражение в перпендикулярной ей плоскости.
Центр симметрии, или центр инверсии, - особая точка внутри фигуры, при отражении в которой фигура совмещается сама с собой.
В кристаллах встречаются оси симметрии только пяти порядков: первого, второго, третьего, четвертого и шестого. Оси пятого порядка, седьмого и выше в кристаллах запрещены, так как их существование несовместимо с представлениями о кристаллической решетке.
Все вышеуказанные операции симметрии называются точечными операциями симметрии, так как они оставляют неизменной, по крайней мере одну точку фигуры.
Полную совокупность элементов симметрии, характеризующую симметрию объекта, называют классом симметрии. Всего существуют 32 точечных класса (группы) симметрии. Это показал в 1867 г. русский инженер и кристаллограф А. В. Гадолин.
В пространственной решетке к рассмотренным элементам симметрии - плоскость симметрии, ось симметрии, центр симметрии - добавляется новый элемент симметрии - трансляция Т=n1a+ n2b+n3c, где n1, n2, n3 - произвольные целые числа, a, b, c -векторы основных (примитивных) трансляций (см. рисунок 2.3).
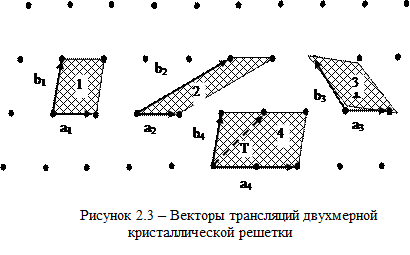
Все изображенные на рисунке пары векторов a и bявляются векторами трансляций решетки. Однако векторы a4 и b4 не являются примитивными векторами трансляций, поскольку вектор трансляции кристаллической решеткиT нельзя выразить как Т=n1a4+ n2b4 где n1 и n2 - целые числа. Все остальные пары векторов a и b можно выбрать в качестве векторов примитивных трансляций. Параллелограммы 1, 2, 3 имеют равную площадь и любой из них можно выбрать в качестве плоской примитивной ячейки.
Трансляция действует не на какую-нибудь точку решетки, а на всю решетку в целом. При перемещении решетки на трансляцию в направлении вектора трансляции решетка совмещается сама с собой всеми своими точками. В 1881 г. выдающийся русский кристаллограф Е. С. Федоров исследовал все мыслимые пространственные расположения частиц кристалла, исходя из того, что плотное заполнение пространства кристаллическими ячейками возможно только при определенной форме ячеек, и установил, что внутри 32 классов симметрии может существовать 230 различных пространственных групп (т. е. 230 типов геометрического расположения атомов в кристаллах). Несколько позже E. С. Федорова к таким же результатам пришел немецкий математик А. Шенфлис.
Французский кристаллограф О. Браве в 1848 г. положил начало геометрической теории структуры кристаллов и показал, что в зависимости от соотношения величины и взаимной ориентации ребер элементарной кристаллической ячейки может существовать 14 типов кристаллических решеток (они получили название решеток Браве).
Различают примитивные (простые), базоцентрированные, объемноцентрированные и гранецентрированные решетки Браве. Если узлы кристаллической решетки расположены только в вершинах параллелепипеда, представляющего собой элементарную ячейку, то такая решетка называется примитивной или простой, если, кроме того, имеются узлы в центре оснований параллелепипеда, то решетка называется базоцентрированной, если есть узел в месте пересечения пространственных диагоналей - решетка называется объемноцентрированной, а если имеются узлы в центре всех боковых граней - гранецентрированной.
По форме ячейки в зависимости от углов между ее гранями a, b, g и в зависимости от соотношения между величиной ребер а, b, с различают семь кристаллических систем (сингоний) (см. таблицу 2.1 ).
Приведем примеры элементарных ячеек четырнадцати простейших кристаллических решеток, принадлежащих разным кристаллическим системам (см. рисунок 2.4 ). На рисунке 2.4 и в таблице 2.1 используются следующие обозначения:
P - символ примитивной ячейки,
I - объемноцентрированной,
F - гранецентрированной,
C - с центрированными основаниями,
R - ромбоэдрической.
Таблица 2.1 - Решетки Браве
| Кубическая | P, I, F | a=b=c | a=b=g=900 | |
| Ромбическая | P, C, I, F | a¹b¹c | a=b=g=900 | |
| Тригональная | R | a=b=c | a=b=g<1200¹900 | |
| Тетрагональная | P, I | a=b¹c | a=b=g=900 | |
| Гексагональная | P | a=b¹c | a=b=900 g=1200 | |
| Моноклинная | P, C | a¹b¹c | a=g=900¹b | |
| Триклинная | P | a¹b¹c | a¹b¹g |
Решетка Браве представляет собой совокупность одинаковых и одинаково расположенных (эквивалентных) атомов или ионов, которые могут быть совмещены друг с другом путем параллельного переноса. Не следует думать, что одна решетка Браве исчерпывает собой все атомы (ионы) данного кристалла. Сложная структура кристаллов может быть представлена как совокупность нескольких решеток Браве, вдвинутых одна в другую. Это одинаково относится как к кристаллам химических элементов, так и к кристаллам сложного химического состава.
 |
Кристаллы правильной многогранной формы встречаются очень редко, так как для роста их требуются особенно благоприятные условия: отсутствие внешних помех, равномерное охлаждение со всех сторон (при росте из расплава) или же равномерный всесторонний приток вещества, отлагающегося на поверхности кристалла (при росте из раствора). Вследствие этого судить о принадлежности кристалла к той или иной кристаллической системе только по его внешней огранке, как правило, бывает довольно трудно. Однако измерение углов между соответствующими гранями кристалла, не имеющего правильной многогранной формы, может дать ответ на вопрос о принадлежности его к определенной кристаллической системе.
Периоды кристаллических решеток (расстояние между ближайшими соседями) для элементов и простейших соединений составляют всего несколько ангстрем, а для сложных неорганических и органических соединений они достигают 10-20 ангстрем. Поэтому наблюдать кристаллическую решетку непосредственно, с помощью оптического или даже электронного микроскопа не представляется возможным. Исключение из этого составляют кристаллы весьма сложных органических соединений - глобулярных белков и вирусов, период решетки которых достигает нескольких сотен ангстрем. Такие кристаллы можно наблюдать с помощью электронного микроскопа.
Не увенчались успехом также попытки доказать решетчатую структуру кристаллов с помощью дифракции света, так как длина световой волны в103-104 раз больше периода решетки. Лишь открытие явления дифракции рентгеновских лучей в кристаллах (1912 г.) явилось прямым доказательством существования кристаллической решетки. С помощью метода рентгенографииможно установить геометрические параметры кристаллической решетки данного кристалла, т. е. найти ребра и углы элементарной ячейки. Таким образом, расшифровка кристаллической структуры вещества имеет сейчас прочную экспериментальную базу - рентгеноструктурный анализ - и не встречает принципиальных затруднений.
Дата добавления: 2021-11-16; просмотров: 627;











