Классификация состояний электронов в атоме
Состояние электрона в атоме определяется четырьмя квантовыми числами: главным n, орбитальным l, магнитным ml и спиновым ms.
Главное квантовое число n определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения, начиная с единицы:
n=1, 2, 3,…
Для атома водорода главное квантовое число определяет энергию атома в стационарном состоянии E(n):
E(n)= R/n2,
где R=13,6 эВ - универсальная постоянная Ридберга.
Состояние электрона в атоме водорода описывается волновой функцией ψ, удовлетворяющей стационарному уравнению Шредингера
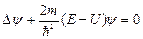 ,
,
где 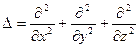 - оператор Лапласа, m - масса частицы, U - потенциальная функция частицы в силовом поле, в котором она движется.
- оператор Лапласа, m - масса частицы, U - потенциальная функция частицы в силовом поле, в котором она движется.
Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z=1), имеет следующий вид:
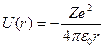 ,
,
где r - расстояние между электроном и ядром.
Решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней
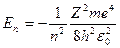 .
.
Самый нижний уровень E1, отвечающий минимальной возможной энергии - основной, все остальные - возбужденные (En > E1). При E<0 движение электрона является связанным - он находится внутри гиперболической потенциальной ямы.
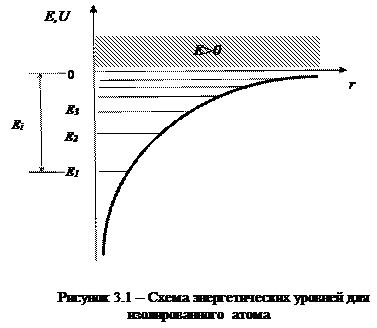 |
Из рисунка 3.1 следует, что по мере роста главного квантового числа n энергетические уровни располагаются теснее и при n=∞ Е∞=0.
При E>0 движение электрона является свободным; область непрерывного спектра E>0 (заштрихована на рисунке 3.1) соответствует ионизированному атому.
Энергия ионизации атома водорода
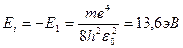 .
.
Орбитальное квантовое число l определяет орбитальный момент количества движения электрона pl:
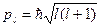 .
.
Квантовое число l может принимать лишь следующий ряд целочисленных значений: l=0,1,2,…(n-1); всего n значений.
Магнитное квантовое число ml определяет ориентацию орбитального момента количества движения pl относительно избранного направления Н(см. рисунок 3.2). Вектор pl может ориентироваться относительно направления Н лишь так, что его проекция на это направление кратна ħ:
plН = mlħ.
Число ml может принимать следующий ряд дискретных значений (всего 2l+1 значений):
ml= -l, -(l-1), …, 0,1,2,…,l.
Спиновое квантовое число ms определяет ориентацию собственного момента количества движения электрона (см. рисунок 3.3) относительно избранного направления Н. Вектор ps может ориентироваться относительно направления Н лишь так, что его проекция на это направление равна (ms может принимать лишь два значения: 1/2 и -1/2.):
psН = msħ.
 |
Поскольку при движении электрона в атоме существенны волновые свойства электрона, квантовая механика вообще отказывается от классического представления об электронных орбитах. Согласно квантовой механике, каждому энергетическому состоянию соответствует волновая функция, квадрат модуля которой определят вероятность обнаружения электрона в единице объема. Вероятность обнаружить электрон в различных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность (густота) которого характеризует вероятность нахождения электрона в различных точках объема атома.
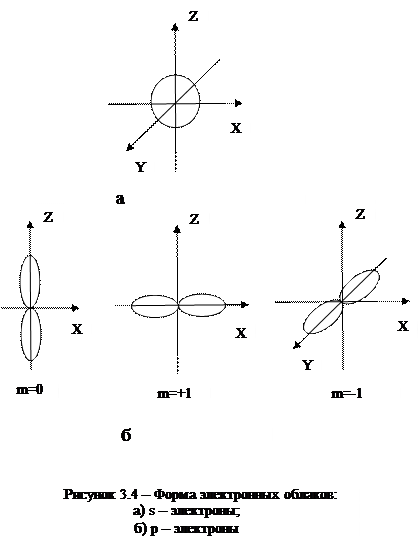
Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число ml характеризует ориентацию облака в пространстве.
Состояние электрона, характеризующееся квантовыми числами l=0, называют s-состоянием, l=1 - р-состоянием, l=2 - d-состоянием, l=3 - f-состоянием и т.д. Электроны, находящиеся в этих состояниях, называются соответственно s-, p-, d-, f- и т.д. электронами.
Значение главного квантового числа указывается перед условным обозначением орбитального квантового числа. Например, электроны в состояниях с n=2 и l=0 и l=1 обозначаются соответственно символами 2s и 2p.
На рисунке 3.4 показана форма электронных облаков и их ориентация для s и p электронов. Распределения плотностей для s-электронов обладают сферической симметрией, тогда как для p-, d-, f-электронов они имеют выраженные направленные области концентрации электронной плотности.
Согласно принципу Паули, в одном и том же атоме, не может быть более одного электрона с одинаковым набором четырех квантовых чисел. Поэтому максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом, равно
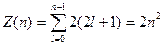 .
.
 |
Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой. В каждой оболочке электроны распределяются по подоболочкам, соответствующим данному l. Поскольку орбитальное квантовое число принимает значения от 0 до n-1, число подоболочек равно порядковому номеру n оболочки. Количество электронов в подоболочке определяется магнитным и спиновым квантовыми числами: максимальное число электронов в подоболочке с данным l равно 2(2l+1). Обозначения оболочек, а также распределение электронов по оболочкам и подоболочкам представлены в таблице 3.1.
Таблица 3.1- Обозначения оболочек и распределение электронов по оболочкам и подоболочкам
| Главное квантовое число n | |||||||||||||||
| Символ оболочки | K | L | M | N | O | ||||||||||
| Максималь-ное число электронов в оболочке | |||||||||||||||
| Орбитальное квантовое число l | |||||||||||||||
| Символ подоболочки | 1s | 2s | 2p | 3s | 3p | 3d | 4s | 4p | 4d | 4f | 5s | 5p | 5d | 5f | 5g |
| Максималь-ное число электронов в подоболочке |
Все уровни s являются невырожденными. Это означает, что каждому из них отвечает единственное состояние электрона в атоме. В соответствии с принципом Паули в таком состоянии могут находиться два электрона, отличающиеся друг от друга направлением своих спинов.
Уровни p являются трехкратно вырожденными: каждому из них отвечает не одно, а три состояния, отличающееся друг от друга магнитным квантовым числом ml. При l=1 оно может принимать следующие три значения: ml= -1;0;+1. Так как в каждом состоянии может находиться два электрона, то для полного комплектования уровня p требуется 6 электронов.
Уровни d имеют пятикратное вырождение, так как при l=2 магнитное квантовое число ml может принимать следующие пять значений: ml= -2; -1; 0;+1;+2. На этом уровне может разместиться 10 электронов.
В общем случае уровень с орбитальным квантовым числом l имеет 2l+1 - кратное вырождение и на нем может разместиться 2(2l+1) электронов.
Дата добавления: 2021-11-16; просмотров: 640;











