Основные соотношения для магнитных цепей

В основу расчета магнитных цепей положен один из фундаментальных законов теории электромагнитного поля – закон полного тока в интегральной форме:

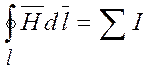, (2.21)

где 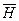– вектор напряженности магнитного поля в произвольной точке замкнутого контура l;

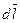– вектор элемента контура в точке, направленный по касательной к контуру;

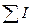– суммарный ток, пронизывающий замкнутый контур «l».

Рассмотрим одноконтурную магнитную систему, состоящую из ферромагнитного сердечника с прямолинейными участками разного поперечного сечения (например, с тремя участками) и воздушным зазором 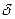(рис. 2.15), которая на одном из участков обхвачена катушкой, имеющей W витков, по которым протекает ток I.

Рис. 2.15

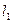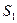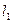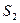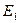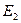Нанесем в магнитопроводе среднюю линию и будем считать, что на первом участке (от точки А до точки В) длиной (по средней линии) поперечное сечение имеет размер , на втором (от точки В через С до D) длина средней линии , а поперечное сечение имеет размер , на третьем участке (от D до и от до А) длина средней линии равна 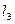, а поперечное сечение 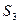и, наконец, на участке воздушного зазора длиной δ поперечное сечение 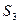(при малой величине δ считают, что весь магнитный поток прилегающего участка проходит в воздухе через сечение, равное сечению этого участка, т.е. пренебрегают вытеснением потока за пределы прилегающего участка).

Отметим, что воздушные зазоры вводятся в замкнутые магнитные системы для обеспечения линейности характеристик устройств (воздух имеет большое магнитное сопротивление).

Очевидно, что напряженность магнитного поля одинакова в пределах каждого участка средней линии, поэтому вместо (2.21) можно записать

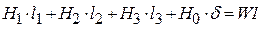или

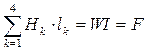. (2.22)

Обобщая полученный результат, для произвольного контура магнитной цепи получим уравнение

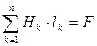, (2.23)

где F = WI – намагничивающая или магнитодвижущая сила, измеряемая в амперах (ампервитках).

Ее направление определяется правилом правого винта (буравчика).

Произведение 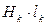в (2.23) рассматривается как разность скалярных магнитных потенциалов или падение магнитного напряжения на коротком участке контура магнитной цепи:

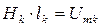. (2.24)

С учетом (2.24) уравнение (2.23) принимает вид:

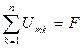(2.25)

и представляет собой аналог второго закона Кирхгофа для контура электрической цепи. Пользуясь такой аналогией, можно изобразить рассматриваемую магнитную цепь так, как показано на рис. 2.16.

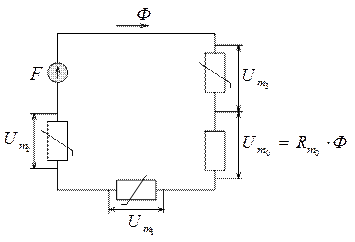
Рис. 2.16

По аналогии с электрическими цепями можно записать закон Ома для любого участка цепи в виде

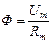, (2.26)

где 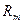– магнитное сопротивление участка магнитной цепи, нелинейно зависящее от магнитного потока.

Магнитная индукция 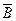и напряженность магнитного поля 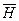связаны соотношением

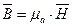, (2.27)

где – абсолютная магнитная проницаемость магнитопровода (сердечника);

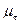– относительная магнитная проницаемость;

– магнитная постоянная или магнитная проницаемость вакуума.

В том случае, когда магнитная цепь имеет разветвление (рис. 2.17), дополнительно применяют интегральную форму выражения принципа непрерывности магнитного поля:

,

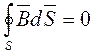согласно которому поток вектора магнитной индукции 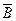через любую замкнутую поверхность равен нулю. Отсюда следует уравнение для узла магнитной цепи

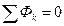. (2.28)

Рис. 2.17

Выражение (2.28) можно рассматривать как первый закон Кирхгофа для магнитной цепи.

Таким образом, основными расчетными соотношениями при исследовании магнитных цепей являются (2.23), (2.24) и (2.28).

Закон Ома (2.26) используется редко из-за трудностей в определении 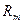. Магнитное сопротивление 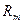можно определить для участков воздушных зазоров, где имеем

, .

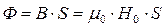Тогда магнитное сопротивление воздушного зазора равно

и имеет размерность .