ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Общие сведения

Электротехнические устройства, установки и системы постоянного тока имеют большое практическое применение на транспорте (двигатели подъемных механизмов, трамваев, троллейбусов, электровозов, электрокаров), при электрохимическом получении металлов (электролизные ванны), в космической технике, в радиоэлектронике, компьютерной технике и т.д. Применение высоковольтных ЛЭП постоянного тока большой протяженности экономически оказывается более целесообразно, чем ЛЭП переменного тока.

Первые шаги электротехники были связаны с освоением энергии постоянного тока, которая вырабатывалась гальваническими элементами.

В настоящее время основными источниками постоянного тока (ИПТ) являются выпрямительные преобразователи (выпрямители), химические аккумуляторы, электромашинные генераторы постоянного тока.

Развиваются и совершенствуются новые виды ИПТ: источники, преобразующие лучистую энергию Солнца при помощи фотоэлементов, являющихся основными источниками электрической энергии космических аппаратов;

- магнитогидродинамические генераторы (МГД-генераторы);

- имеются сообщения о создании в США электрохимических ИПТ для электромобилей, в которых электрическая энергия получается в результате реакции кислорода атмосферного воздуха с бензиновым топливом.

В электротехнике решаются две задачи:

- синтез электротехнических устройств;

- анализ этих устройств.

Задача синтеза решается при создании новых устройств конструкторами. Это наиболее сложная задача. Анализ работы электроустройств чаще всего необходимо проводить уже при их эксплуатации, поэтому существуют типовые задачи анализа.

Как правило, задача анализа состоит в определении токов и напряжений на всех участках электрической цепи. При этом конфигурация цепи и параметры ее элементов (ВАХ источников и потребителей энергии, электрические сопротивления токопроводов и др.) считаются известными.

Как уже отмечалось, при анализе (расчете режима работы) электрической цепи необходимо эту цепь представить и изобразить графически схемой, в которой элементы электрической цепи представлены в виде соединений идеализированных элементов — резистивного R, индуктивного L, и емкостного С, а источники электрической энергии представляются как последовательное соединение ЭДС и внутренних сопротивлений этих источников.

Однако при анализе электрических цепей постоянного тока, пассивными элементами схем являются только резистивные элементы, т.к. сопротивления индуктивных элементов ( 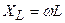) постоянному току равны нулю, а сопротивления емкостных элементов ( 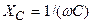)при этом равны бесконечности, так что емкостные элементы разрывают электрические цепи постоянного тока.

Законы Кирхгофа

Законы Кирхгофа лежат в основе анализа электрических цепей.

2.2.1 Первый закон Кирхгофа. Алгебраическая сумма токов в узле электрической цепи равна нулю. Математически это записывается так:

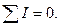(2.1)

Всем токам, направленным от узла, в уравнении (2.1) приписывается одинаковый знак, например, положительный, тогда все токи, направленные к узлу, войдут в уравнение с отрицательным знаком.

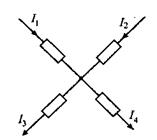
Рис. 2.1. Иллюстрация к первому закону Кирхгофа

На рисунке 2.1 показан узел, в котором сходятся четыре ветви. Уравнение (2.1) в этом случае принимает вид:

– I₁ – I₂ + I₃ + I₄ = 0.

Первый закон Кирхгофа отражает тот факт, что в узле электрический заряд не накапливается и не расходуется. Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени.

2.2.2 Второй закон Кирхгофа. Алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме напряжений на элементах этого контура:

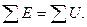(2.2)

Если в рассматриваемом контуре отсутствуют ЭДС, то уравнение (2.2) принимает вид:

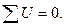(2.3)

Обход контура совершается в произвольно выбранном направлении. При этом ЭДС и напряжения, совпадающие с направлением обхода, берутся с одинаковыми знаками, например, со знаками «+».

Например, для схемы (рис. 2.2) имеем

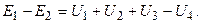
Второй закон Кирхгофа можно применять и для контуров, которые состоят не только из участков схемы, но и из напряжений между какими-либо точками схемы.

Так для контура 4-5-3-6-4, состоящего из участка цепи 4-5-3 и напряжения 4-6-3, можно составить уравнение

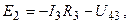
где U₄₃ – напряжение между точками 4 и 3 схемы, В.

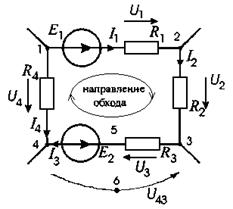
Рис. 2.2. Иллюстрация ко второму закону Кирхгофа