Из упорядоченного в неупорядоченное состояние
Еще до возникновения статистической термодинамики и даже до перехода к молекулярно-кинетическим представлениям о природе теплоты были известны два основных закона термодинамики, которые обобщали известные к тому времени опытные факты. Один их них - первое начало термодинамики - являлся фактически законом сохранения энергии и формулировался следующим образом: количество теплоты Q, сообщенное системе (например, газу), равно сумме приращения ее внутренней энергии 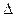 U и совершенной механической работы A:
U и совершенной механической работы A:
Q = 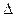 U + A. (2.4.2)
U + A. (2.4.2)
Этот закон, однако, ничего не говорил о направлении протекания тепловых процессов. Например, ему не противоречит замерзание некоторого объема воды, помещенного в раскаленную печку. Необратимость тепловых процессов отражает специальный закон -второе начало термодинамики,имеющий несколько эквивалентных формулировок, таких как:
- тепло не может самопроизвольно перетекать от холодного тела к горячему;
- нельзя построить вечный двигатель 2-го рода, который совершал бы полезную работу только за счет охлаждения теплового резервуара;
- энтропия замкнутой системы является неубывающей функцией, т. е. при любом реальном процессе она либо возрастает, либо остается неизменной.
Понятие энтропии, введенной в термодинамику Клаузиусом, носило первоначально искусственный характер. Знаменитый французский ученый А. Пуанкаре писал по этому поводу:
«Энтропия представляется несколько таинственной в том смысле, что величина эта недоступна ни одному из наших чувств, хотя и обладает действительным свойством физических величин, потому что по крайней мере в принципе вполне поддается измерению».
По определению Клаузиуса, энтропией называется такая физическая величина, приращение которой 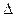 S равно количеству тепла
S равно количеству тепла 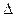 Q, полученному системой, деленному на абсолютную температуру
Q, полученному системой, деленному на абсолютную температуру
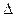 S =
S = 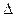 Q / T. (2.4.3)
Q / T. (2.4.3)
Если два тела, имеющие разные температуры Т1 и Т2 (Т1>Т2), привести в тепловой контакт, то изменение энтропии этой системы 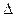 S будет складываться из изменения энтропии первого тела
S будет складываться из изменения энтропии первого тела 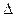 S1 и изменения энтропии второго тела
S1 и изменения энтропии второго тела 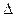 S2:
S2: 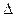 S =
S = 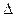 S1 +
S1 + 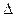 S2. Пусть первое тело, как более горячее, отдает второму небольшое количество тепла
S2. Пусть первое тело, как более горячее, отдает второму небольшое количество тепла 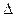 Q, тогда
Q, тогда 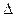 S1 = -
S1 = - 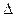 Q/T1,
Q/T1, 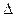 S2 =
S2 = 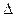 Q/T2,
Q/T2, 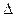 S =
S = 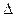 Q (1/T2 - 1/T1) >0. Таким образом, при перетекании тепла от горячего тела к холодному энтропия системы, действительно, возрастает. А.Пуанкаре отмечал:
Q (1/T2 - 1/T1) >0. Таким образом, при перетекании тепла от горячего тела к холодному энтропия системы, действительно, возрастает. А.Пуанкаре отмечал:
«Энтропия является, следовательно, величиной, в некотором роде измеряющей эволюцию данной системы или по крайней мере указывающей направление этой эволюции».
Физическая сущность понятия энтропии была «вскрыта» статистической механикой. Оказалось, что энтропия S - это не что иное как умноженный на постоянную Больцмана k = 1,38 × 10-23 Дж/К натуральный логарифм вероятности Р данного состояния макроскопической системы
S = k lnP. (2.4.4)
При таком определении энтропии становится понятным, что возрастание энтропии замкнутой системы - это всего лишь естественный переход системы в наиболее вероятное состояние. С понятием вероятности состояния, а следовательно, с энтропией связано представление об упорядоченности системы. Чем больше порядок в системе (например, все молекулы идеального газа находятся в одной точке пространства), тем меньше ее энтропия и меньше вероятность такого состояния. Наоборот, чем меньше упорядочена система - тем больше ее энтропия, больше вероятность такого состояния. Таким образом, статистический смысл второго начала термодинамики заключается в том, что изолированные системы самопроизвольно переходят из упорядоченного в неупорядоченные состояния. М.Планк писал:
« Принцип сохранения энергии ограничивает течение явлений природы, допуская только превращения энергии, а не созидание или уничтожение ее. Второе начало в этом отношении идет еще дальше и допускает не все виды превращений, а только определенные превращения при определенных условиях».
Дата добавления: 2018-05-10; просмотров: 1503;











