Альфа-бета-процедура

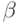Теоретически, это эквивалентная минимаксу процедура, с помощью которой всегда получается такой же результат, но заметно быстрее, так как целые части дерева исключаются без проведения анализа. В основе этой процедуры лежит идея Дж. Маккарти об использовании двух переменных, обозначенных и (1961 год).

Основная идея метода состоит в сравнении наилучших оценок, полученных для полностью изученных ветвей, с наилучшими предполагаемыми оценками для оставшихся. Можно показать, что при определенных условиях некоторые вычисления являются лишними. Рассмотрим идею отсечения на примере рис. 3.6. Предположим, позиция А полностью проанализирована и найдено значение ее оценки 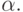Допустим, что один ход из позиции Y приводит к позиции Z, оценка которой по методу минимаксаравна z. Предположим, что 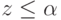. После анализа узла Z, когда справедливо соотношение , ветви дерева, выходящие из узла Y, могут быть отброшены (альфа-отсечение).

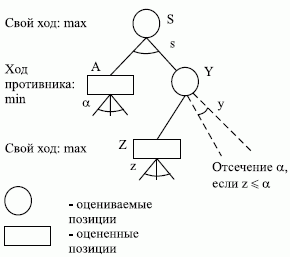
Рис. 3.6.- отсечение

Если мы захотим опуститься до узла Z, лежащего на уровне произвольной глубины, принадлежащей той же стороне, что и уровень S, то необходимо учитывать минимальное значение оценки 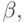получаемой на ходах противника.

Отсечение типа 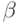можно выполнить всякий раз, когда оценка позиции, возникающая после хода противника, превышает значение 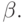Алгоритм поиска строится так, что оценки своих ходов и ходов противника сравниваются при анализе дерева с величинами и 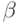соответственно. В начале вычислений этим величинам присваиваются значения и , а затем, по мере продвижения к корню дерева, находится оценка начальной позиции и наилучший ход для одного из противников.

Правила вычисления и 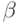в процессе поиска рекомендуются следующие:

1. у MAX вершины значение равно наибольшему в данный момент значению среди окончательных возвращенных значений для ее дочерних вершин;

2. у MIN вершины значение 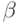равно наименьшему в данный момент значению среди окончательных возвращенных значений для ее дочерних вершин.

Правила прекращения поиска:

3. можно не проводить поиска на поддереве, растущем из всякой MIN вершины, у которой значение 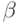не превышает значения всех ее родительских MAX вершин;

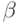4. можно не проводить поиска на поддереве, растущем из всякой MAX вершины, у которой значение не меньше значения всех ее родительских MIN вершин.

На рис. 3.7 показаны отсечения для конкретного примера. Таким образом, -алгоритм дает тот же результат, что и метод минимакса, но выполняется быстрее.

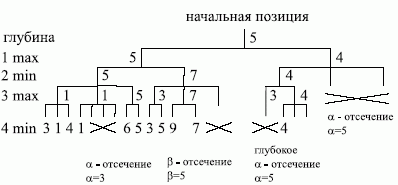
Рис. 3.7.a-b отсечение для конкретного примера

Использование алгоритмов эвристического поиска для поиска на графе И, ИЛИ выигрышной стратегии в более сложных задачах и играх (шашки, шахматы) не реален. По некоторым оценкам игровое дерево игры в шашки содержит 10⁴⁰ вершин, в шахматах 10¹²⁰вершин. Если при игре в шашки для одной вершины требуется 1/3 наносекунды, то всего игрового времени потребуется 10²¹ веков. В таких случаях вводятся искусственные условия остановки, основанные на таких факторах, как наибольшая допустимая глубина вершин в дереве поиска или ограничения на время и объем памяти.

Многие из рассмотренных выше идей были использованы А. Ньюэллом, Дж. Шоу и Г. Саймоном в их программе GPS. Процесс работы GPS в общем воспроизводит методы решения задач, применяемые человеком: выдвигаются подцели, приближающие к решению; применяется эвристический метод (один, другой и т. д.), пока не будет получено решение. Попытки прекращаются, если получить решение не удается.

Программа STRIPS (STanford Research Institut Problem Solver) вырабатывает соответствующий порядок действий робота в зависимости от поставленной цели. Программа способна обучаться на опыте решения предыдущих задач. Большая часть игровых программ также обучается в процессе работы. Например, знаменитая шашечная программа Самюэля, выигравшая в 1974 году у чемпиона мира, "заучивала наизусть" выигранные партии и обобщала их для извлечения пользы из прошлого опыта. Программа HACHER Зуссмана, управляющая поведением робота, обучалась также и на ошибках.