РОЗРАХУНКИ ПРИПУСТИМИХ ЗУСИЛЬ І МОМЕНТІВ

При розробці технології потрібно знати припустимі зусилля і моменти прокатки для кожної кліті. За звичай ці параметри вказуються у технологічній інструкції, але не завжди точно, оскільки вони дещо залежать від сортаменту продукції і настройки приводу, які змінюються. Тому для точного визначення припустимих параметрів прокатки потрібно їх визначати для кожного випадку окремо.

Для визначення припустимої сили прокатки в клітях дуо рекомендується використовувати добре апробовану методику А.І.Целікова, яка ґрунтується на таких передумовах:

- валок вважається балкою змінного перетину;

- ця балка спирається на шарнірні опори;

- рівнодіюча зусилля прокатки прикладена до центру бочки.

Розрахункова схема наведена на рис. 6.1.

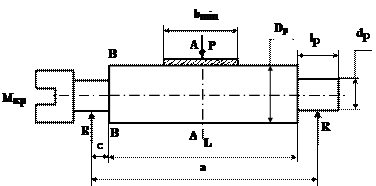Рисунок 6.1 – Розрахункова схема валкового комплекту дуо

Небезпечними перетинами у валка є центр бочки (пер. А-А) і місце переходу бочки в шийку з боку привода (пер. В-В).

Припустима сила прокатки по перетину А-А:

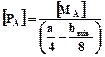(6.1)

де 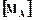- припустимий момент згину в перетині А-А, МНмм;

b_min – мінімальна ширина розкату, що прокатується, мм.

,

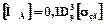де 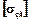- припустима напруга на згин для металу валка, МН/мм².

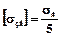. (6.2)

Для навчальної мети рекомендуються такі значення межі міцності:

а) для валків із чавуну: σ_в = 350÷400 МПа;

б) для валків із литої вуглецевої сталі: σ_в = 500÷600 МПа ;

в) для валків із кованої вуглецевої сталі: σ_в = 600÷650 МПа ;

д) для валків із кованої легованої сталі: σ_в = 700÷750 МПа .

При реальних розрахунках σ_в визначається з урахуванням виду термообробки, розміру валків (масштабний фактор) і якості обробки поверхні валків (див. наприклад [11]).

Припустима сила прокатки по перетину В-В:

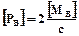, (6.3)

де 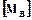- припустимий момент згину в перетині В-В, МНмм:

,

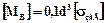де 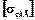- припустима напруга згину в перетині В-В, МНмм. Оскільки в перетині В-В має місце складний опір (напруга згину від сили прокатки Р і напруга кручення від моменту двигуна М_кр), то 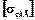визначається по еквівалентній напрузі. Для стальних валків еквівалентна напруга розраховується по 4-й теорії міцності:

,

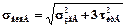де напруга кручення дорівнює:

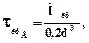МПа. (6.4)

Отже в цьому випадку:

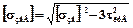,(6.5)

оскільки еквівалента напруга не може перевищувати припустиму по (6.2).

Для валків із чавуну еквівалентна напруга визначається по теорії міцності Мора:

.

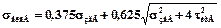В цьому разі для визначення припустимої 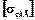потрібно вирішити квадратне рівняння:

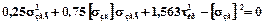
Одним із коренів цього рівняння буде :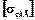

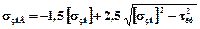(6.6)

Приклад розрахунку припустимої сили прокатки для чорнової кліті дуо ТЛС 2250. Вихідні дані: D_p = 940мм, L_б = 2500мм; d_p = 640мм; l_р = 690мм; b_min = 1100мм; М_кр = 0,958МНм, матеріал – чавун.

Припустима напруга на згин для металу валка:

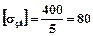МПа.

Припустимий момент згину в перетині А-А:

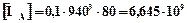Нмм.

Припустима сила прокатки по перетину А-А:

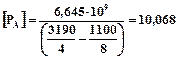МН,

де відстань між вісями натискних гвинтів а знаходиться з того, що реакції R прикладені до середини шийок валків: .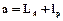

Напруга кручення в перетині В-В:

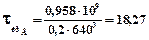МПа.

Припустима напруга на згин в перетині В-В:

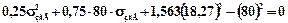
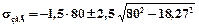
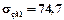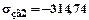МПа; МПа.

Очевидно, що 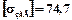МПа.Момент згину в В-В:

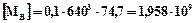Нмм.

Припустима сила прокатки по перетину В-В:

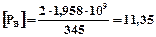МН.

Отже в даному випадку припустима сила прокатки [Р] = 10,1 МПа. Але слід мати на увазі, що цей параметр в клітях дуо суттєво залежить від моменту прокатки. Так, при максимальному моменту прокатки для цієї кліті 2,32МНм (Див. додаток В), 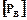= 7,1МН. Отже і [Р] = 7,1МН. А оскільки момент прокатки у кожному проході різний, то і припустима сила прокатки буде різна.

На відміну від клітей дуо, у клітей кварто [Р]залежить тільки від параметрів валкової системи. В небезпечних перетинах намає складного напруженого стану і тому сила [Р] визначається тільки по напругам згину опорного валка. На рис. 6.2 - розрахункова схема:

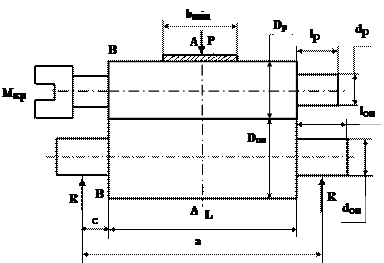Рисунок 6.2 – Розрахункова схема валкового комплекту кварто

При визначенні припустимої сили [Р]по перетину А-А слід мати на увазі, що всі 100% сили прокатки сприймаються опорними валками. В деяких підручниках, наприклад [12], помилково вказується, що опорні валки сприймають приблизно 39/40 цієї сили, а робочі – 1/39. Але шийки опорних валків не спираються на натискні гвинти, і тому робочі валки не передають нагрузку на станини.

Припустима сила [Р]по перетину А-А визначається по (6.1), але

замість b_man слід підставляти L_б, оскільки опорний валок контактує з робочим по всій довжині бочки опорного валка. Припустима сила прокатки по перетину В-В визначається по (6.3), але 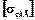буде дорівнювати .

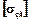Приклад розрахунку припустимої сили прокатки для чистової кліті кварто ТЛС 3000. Вихідні дані: D_p = 900мм, (D_оп)_min=1500ммL_оп = 3000мм; d_оп = 950мм; l_оп = 690мм; матеріал опорних валків – легована сталь.

Припустима напруга на згин для металу валка:

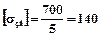МПа.

Припустимий момент згину в перетині А-А:

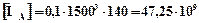Нмм,

де діаметр опорних валків слід брати мінімальний, після всіх переточок. Припустима сила прокатки по перетину А-А:

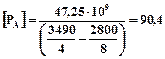МН,

де відстань між вісями натискних гвинтів а знаходиться з того, що реакції R прикладені до середини шийок валків: .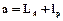

Момент згину в В-В:

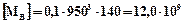Нмм.

Припустима сила прокатки по перетину В-В:

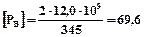МН.

Отже в даному випадку припустима сила [Р] = 69,6МН, і вона не залежить від параметрів прокатки.

При визначенні припустимих моментів слід розрізняти припустимий момент по напругам кручення у приводному кінці робочого валка [М_кр]і припустимий момент прокатки по потужності двигуна (або двигунів при цндивідуальному приводі).

Перший знаходиться досить просто:

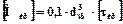Нм, (6.7)

де d_пр – діаметр приводного кінця валка (по дну шлицевих пазів, якщо вони є);

[τ_кр] – прпустима напруга на кручення металу валка:

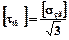, МПа. (6.8)

Зрозуміло, що 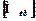повинен витримувати і шпиндель.

Значно складніше визначається припустимий момент прокатки по потужності двигуна. Відомо, що для можливості прокатки повинно виконуватись співвідношення:

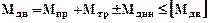,(6.9)

де М_дв – момент, що розвивається двигуном (або двигунами), МНм;

М_пр – момент прокатки (пластичної деформації металу), МНм;

М_тр – момент тертя в підшипниках валів, МНм;

М_дін – динамічний момент приводу, МНм;

[М_дв] – припустимий момент двигуна у даному проході, МНм.

Методи визначення М_пр розглядаються у наступному розділі. Момент тертя у клітях дуо:

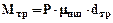,(6.10)

де μ_пш – коефіцієнт тертя в підшипниках. Орієнтовно можна використовувати наступні значення [12]:

Для підшипників з текстолітовими вкладишами – 0,01÷0,03

Для підшипників гідродинамічних – 0,003

Для підшипників кочення з конічними роликами – 0, 01÷0,02

d_тр – діаметр тертя в підшипниках. Для підшипників ковзання він дорівнює діаметру шийки, а у підшипників кочення - середньому між зовнішнім і внутрішнім діаметрами підшипника.

У клітей кварто основні втрати на тертя відбуваються в підшипниках опорних валків, але оскільки привід йде через робочі валки, то:

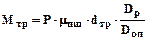(6.11)

Динамічний момент привода :

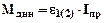,(6.12)

де ε₁₍₂₎ – кутове прискорення (уповільнення) валків, с^-1;

І_пр - момент інерції деталей приводу, приведений до вісей робочих валків, кгм².

Як відомо, момент інерціі, це:

,

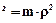де m – маса тіла, що обертається, кг;

ρ – радіус інерції, м. Радіус інерції – це радіус еквівалентного циліндра (або кулі), вистроєного навколо даної вісі, який має такий же мометн інерції і масу відносно цієї вісі, що і дане тіло. Наприклад, для суцільного однорідного циліндра:

,

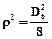де D_ц – геометричний діаметр циліндра.

У технічних системахі одиниць замість моменту інерції використовувався т.з. маховий момент, рівний GD², де G– вага деталі в кгс, а D– геометричний діаметр деталі, м. Іноді маховим моментом називають параметр mD², де m – маса деталі, в кг. Співвідношення між моментом інерції в системі Si і маховим моментом: 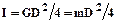, оскільки чисельні величини GD² в кгс·м² і mD²в кг·м² рівні. Ці співвідношення приходиться використовувати при визначенні моменту інерції якоря двигунів, оскільки у більшості довідників він наведений у махових моментах.

Момент інерції тіла складної форми визначається розбиттям його на частки з простими формами:

,

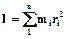деr_i – радіус інерції і-тої частки. Таким чином для знаходження І складного по геометії тіла потрібно визначити моменти інерції його частин відностно даної вісі і скласти їх. Моменти великої кількості тіл елементарних форм можна знайти по довіднику [13].

Моменти інерції всіх мас, що обертаються, слід привести до валу двигуна, якщо привід груповий, або двигунів, коли він індивідуальний. Приведенні відбувається по балансу кінетичної енергії. Наприклад, для кліті кварто з індивідуальним приводом (рис.6.3):

Рисунок 6.3 – Схема індивідуального приводу кліті кварто

,

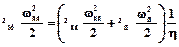де І_пр – момент інерції приводу, приведений до валу двигуна, кгм²;

І_дв – момент інерції деталей на валу двигуна (якоря 4, муфти, промвала 3, шпинделя 2, робочого валка), кгм²;

І_оп – момент інерції опорного валка 1, кгм²;

ω_дв – частота обертання вала двигуна, с^-1;

ω_оп – частота обертання опорного валка, с^-1;

η – к.к.д. приводу.

Звідси:

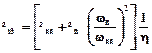. (6.13)

Наприклад: визначити момент інерції групового приводу чистової кліті ТЛС 2800 (рис.6.4).

Рисунок 6.4 – Схема групового приводу кліті кварто

Момент інерції приводу складається з суми моментів інерції робочих валків 1, приведених до вісі робочих валків моментів опорних валків 2, моментів муфт з лопаттю 3, які з′єднують робочі валки із шпінделями, моментів шпінделів 3 та шестеренних валків 4, моторної муфти 5 і моменту інерції якоря двигуна 6.

Для визначення моменту інерції робочого валка по його креслен-

ню ця деталь розбивається на ряд менших частин з простими формами (циліндри і конуси). Розраховуються моменти інерції цих частин і визначається їх сума, яка і є моментом інерції всієї деталі. Наприклад, момент інерції бочки:

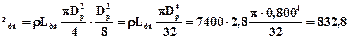кгм²,

де ρ = 7400кг/м³ – щільність матеріалу валка – чавуну.

Аналогічно вираховуються моменти інерції інших деталей приводу. В результаті:

1. Момент інерції робочого валка І_р = 1007,6кгм²;

2. Момент інерції опорного валка І_оп = 9392,1кгм²;

3. Момент інерції муфти з лопаттю І_мл =292,5кгм²;

4. Момент інерції шпінделя І_шп = 908,5кгм²;

5. Момент інерції шестеренного валка І_шв = 1575,8кгм²;

6. Момент інерції моторної муфти І_м = 17397,1кгм²;

7. Момент інерції якоря двигуна:

І_яд = 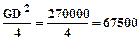кгм²,

де GD² = 270тс·м² – маховий момент якоря у технічній системі одиниць.

Приведений до валу двигуна момент інерції робочого і опорного валків:

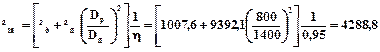кгм²,

де к.к.д механічної передачі η = 0,95.

Момент інерції приводу чистової кліті стана 2800:

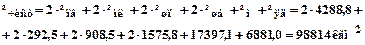
Сумарний момент по (6.9) не повинен перевищувати припустимий [М_дв], який в змозі розвинути двигун при даній швидкості. Найбільший момент двигуну потрібно розвивати при розгоні з металом у валках, причому цей момент буде постійним:

,

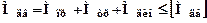У такому разі двигуни як постійного струму, так і синхронний, будуть працювати у режимі змінної потужності (рис. 6.5):

Рисунок 6.5 – Змінення параметрів приводу у режимі змінної потужності

При роботі у першій зоні регулювання, де ω ≤ ω_н, зменшення кутової швидкості відбувається за рахунок зменшення напруги у силовому ланцюзі. Струм якоря при цьому незмінний, потужність росте пропорційно моменту. При переході у другу зону регулювання, коли ω > ω_н,підвищення швидкості досягається зменшенням напруги у ланцюзі збудження, що веде до зменшення магнітного потоку [15]. Тому для збереження моменту на валу двигуна струм якоря повинен зростати пропорційно швидкості, отже віддавана потужність повинна зростати. Але потужність любого двигуна обмежена і припустима межа зростання N характеризується коефіцієнтом перевантаження. Тому:

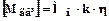, (6.14)

де М_н – номінальній момент двигуна, МНм;

k - коефіцієнт перевантаження. Для прокатних двигунів на початку розгону k = 2,5÷3,0; на максимаьній швидкості по умовам комутації – 1,5. При розрахунках беруть середню величину 2,0÷2,25.

η– к.п.д. лінії приводу. Визначається розрахунком.

Оскільки у другій зоні регулювання струм якоря значно перевищує номінальний, на який розрахована система охолодження двигуна, то обмотка не буде перегріватись тільки завдяки паузам при прокатці. Але чи достатня для цього тривалість пауз - перевіряється розрахунком двигуна на перегрівання.

При недостатній потужності двигуна можлива робота у режимі постійного струму (рис. 6.6).

		ω

Рисунок 6.6 – Змінення параметрів приводу у режимі постійного струму

Якщо струм якоря не змінювати, то при переході у другу зону

регулювання момент двигуна буде зменшуватись зворотньо пропорційно збільшенню швидкості і припустимий момент буде:

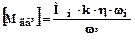, (6.15)

де ω_і – максимальна швидкість у даному проході.

Отже в цьому режимі перегрівання обмотки буде тільки за рахунок коефіцієнта перевантаження k. Тепловий режим буде менш напруженим, але й цикл прокатки збільшиться через зменшення припустимих обтисків при зменшенні припустимих моментів.

У синхронних двигунів змінення швидкості обертання ротора відбувається за рахунок змінення частоти коливань струму. Але момент у них залежить від кутової швидкості також по (6.14, 6.15).