Именно эти три фактора и приводят к особенностям проявления высших гармоник в трехфазных цепях.

В определённой степени здесь мы сталкиваемся с явлениями, которые были рассмотрены в случае питания трёхфазных цепей от источника с несимметричной системой ЭДС и разложения этой системы на симметричные составляющие.

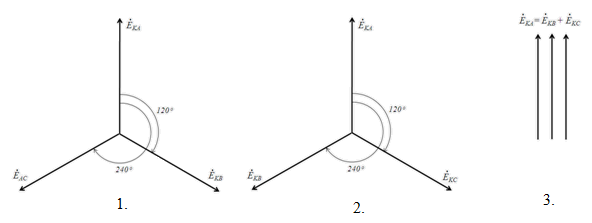
Рис.64

Если не касаться конструктивных особенностей трехфазных трансформаторов, что является прерогативой курса электрических машин, а ограничить рассмотрение этих устройств только анализом электромагнитных процессов в них с точки зрения теоретической электротехники, работу трехфазных трансформаторов, как уже было отмечено, можно свести к совместной работе трех рассмотренных ранее однофазных трансформаторов на общую электрическую цепь. Обмотки этих трансформаторов соединяются либо по схеме «звезда», либо по схеме треугольника, при этом вторичные обмотки каждого из них входят как составная часть фаз «A», «B» и «C» в единую сеть в качестве фазных ЭДС 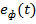, либо фазных напряжений 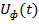. Упрощенная схема замещения вторичной обмотки трансформатора (источника вторичного питания) в случае соединения фаз обмоток по схеме «треугольник» представлена на рис. 65.

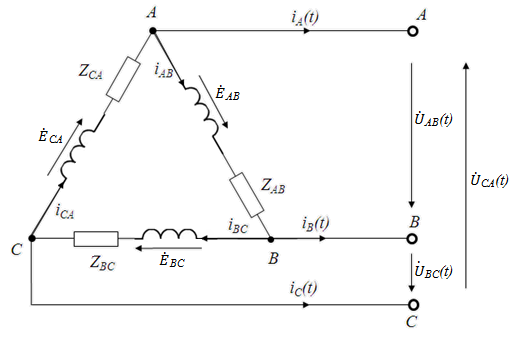
Рис. 63.

Рассмотрим работу трансформатора на холостом ходу. В этом случае 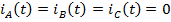, т.е. линейные токи на всех гармониках отсутствуют. Фазные токи формируются фазными ЭДС. Понятно, что .

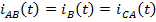Как было отмечено, постоянные составляющие в фазных ЭДС, как и четные гармоники в кривых токов и напряжений отсутствуют.

В соответствии со вторым законом Кирхгофа для замкнутого контура «треугольника» на каждой К-той гармонике имеем (*)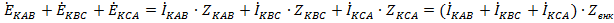

Понятно, что внутренние сопротивления каждой обмотки во всех фазах одинаковы, т.е. 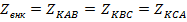. Напряжения на фазах (в данном случае линейные напряжения) отличаются от соответствующих ЭДС на величину падения напряжения на внутренних сопротивлениях, т.е.

,

,

(**)

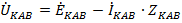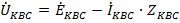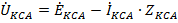Понятно, что для симметричных систем прямого и обратного чередования фаз фазные ЭДС на каждой гармонике одинаковы по величине и смещены друг относительно друга на 120°, т.е. их сумма равна нулю, т.е. .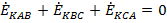

Это значит, что 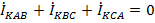, т.е. в режиме холостого хода трансформатора (источника питания) токи прямой и обратной последовательности, как это и следует из общепринятого определения режима холостого хода источника, будут равны нулю.

В то же время суммы совпадающих по фазе ЭДС и фазных токов гармоник, кратных трем, будут отличаться от нуля. При этом

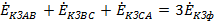и .

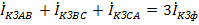Это значит, что даже на холостом ходу нагрузка отключена трехфазный трансформатор будет нагружен током третьих гармоник. По (*) этот ток равен

(***).

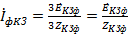Действующее значение циркулирующего в фазах тока гармоник, кратных трем, в общем случае, равно .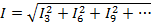

В связи с тем, что в трехфазных цепях четные гармоники отсутствуют, а влияние гармоник с номером 9 и выше ничтожно, амперметр, включенный в разрыв треугольника вторичной обмотки фактически зафиксирует только действующие значения третьей, наиболее значимой, гармоники .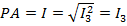

Суммарное действующее значение ЭДС третьих гармоник может быть измерено включенным в разрыв треугольника вольтметром. При этом действующее значение третьей гармоники одной фазы .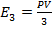

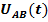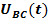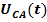В линейных напряжениях , и в соответствии с (**) в полной мере будут представлены напряжения и прямого и обратного чередования фаз. Однако, гармоники, кратные трем, в этих напряжениях будут отсутствовать. Например, для напряжения 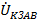в соответствии с (**) имеем 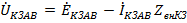(****), но в связи с (***) для фазы АВ имеем 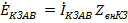, что превращает равенство (****) в ноль: ЭДС каждой фазы гармоники, кратной трем, в связи с наличием в фазе тока третьей гармоники полностью компенсируется падением напряжения на внутреннем сопротивлении фазы. Это значит, что гармоники, кратные трем, в линейном напряжении питания трехфазной цепи отсутствуют.

При этом следует четко понимать, что это утверждение относится только к случаям, когда учитываются сопротивления обмоток фаз генератора (трансформатора).

Упрощенная схема вторичной обмотки трехфазного трансформатора при соединении фаз по схеме «звезда» представлена на рис. 66.

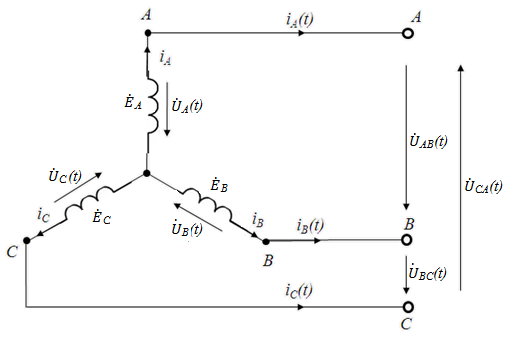
Рис. 66

Понятно, что в режиме холостого хода внешняя цепь разомкнута. Это значит, что фазные и линейные токи всех гармоник, включая и совпадающие по фазе токи гармоник, кратных трем, будут равны нулю. В этом случае режим холостого хода источника питания в полной мере соответствует смыслу этого режима.

Что касается фазных напряжени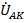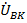й , и 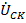, для симметричных систем прямого и обратного чередования фаз их сумма (рис. 66) равна нулю. В то же время сумма напряжений совпадающих по фазе гармоник, кратных трем будет равна утроенному напряжению третьей гармоники фазы, т.е. .

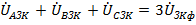Это означает, что даже в симметричной трехфазной системе потенциал нейтральной точки «N» вторичной обмотки трансформатора не будет равен нулю, что следует обязательно учитывать при формировании заземлений в цепи.

В соответствии со вторым законом Кирхгофа линейное напряжение при рассматриваемой цепи равно разности соответствующих фазных напряжений. Это относится не только к напряжениям 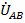, 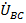и 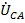, но и к каждой из гармоник, т.е. 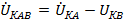, 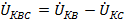и .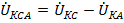

Понятно, что для симметричных систем напряжений с прямым и обратным чередованием фаз линейные напряжения для каждой из гармоник на векторной диаграмме образуют равносторонний треугольник, связанный с равновеликой трехлучевой звездой соответствующих фазных напряжений. Связь между этими напряжениями формируется обычными правилами для симметричных трехфазных систем. Например, при прямом чередовании фаз 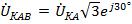, а при обратном, .

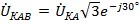Однако, совпадающие по величине и фазе фазные напряжения гармоник, кратных трем при вычитании просто взаимно уничтожаются. Это значит, что в линейном напряжении гармоники, кратные трем, отсутствуют, что приводит к тому, что соотношение между действующими значениями фазных напряжений на зажимах симметричного генератора при наличии высших гармоник 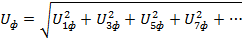и линейных 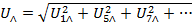в связи с отсутствием в линейных гармоник, кратных трем, оказывается 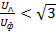. Следовательно, при фазном напряжении, например, 220В линейное напряжение на входе трехфазной цепи может оказаться заметно меньшим стандартных для этого случая 320В, что приведет, в частности, к падению мощности трехфазных двигателей.