Определение оптимального уровня денежных средств

Денежные средства предприятия включают в себя деньги в кассе и на расчётном счёте в коммерческих банках. Возникает вопрос: почему эти наличные средства остаются свободными, а не используются, например, для покупки ценных бумаг, приносящих доход в виде процента? Ответ заключается в том, что денежные средства более ликвидны, чем ценные бумаги. В частности, облигацией невозможно расплатиться в магазине, такси и т.п.

Различные виды текущих активов обладают различной ликвидностью, под которой понимают временный период, необходимый для конвертации данного актива в денежные средства, и расходы по обеспечению этой конвертации. Только денежным средствам присуща абсолютная ликвидность. Для того чтобы вовремя оплачивать счета поставщиков, предприятие должно обладать определённым уровнем абсолютной ликвидности. Его поддержание связано с некоторыми расходами, точный расчёт которых в принципе невозможен. Поэтому принято в качестве цены за поддержание необходимого уровня ликвидности принимать возможный доход от инвестирования среднего остатка денежных средств в государственные бумаги. Основанием для такого решения является предпосылка, что государственные ценные бумаги безрисковые, точнее степенью риска, связанного с ними можно пренебречь. Таким образом, деньги и подобные ценные бумаги относятся к классу активов с одинаковой степенью риска, следовательно, доход (издержки) по ним является сопоставимым.

Однако вышеизложенное не означает, что запас денежных средств не имеет верхнего предела. Дело в том, что цена ликвидности увеличивается по мере того, как возрастает запас наличных денег. Если доля денежных средств в активах предприятия невысокая, небольшой дополнительный приток их может быть крайне полезен, в обратном случае наоборот. Перед финансовым менеджером стоит задача определить размер запаса денежных средств исходя их того, чтобы цена ликвидности не превысила маржинального процентного дохода по государственным ценным бумагам.

С позиции теории инвестирования денежные средства представляют собой один из частных случаев инвестирования в товарно-материальные ценности. Поэтому к ним применимы общие требования. Во-первых, необходим базовый запас денежных средств для выполнения текущих расчётов. Во-вторых, необходимы определённые денежные средства для покрытия непредвиденных расходов. В-третьих, целесообразно иметь определённую величину свободных денежных средств для обеспечения возможного или прогнозируемого расширения деятельности.

Таким образом, к денежным средствам могут быть применены модели, разработанные в теории управления запасами и позволяющие оптимизировать величину денежных средств. Речь идёт о том, чтобы оценить:

1. Общий объём денежных средств и их эквивалентов;

2. Какую их долю следует держать на расчётном счёте, а какую в виде быстрореализуемых ценных бумаг;

3. Когда и в каком объёме осуществлять взаимную трансформацию денежных средств и быстрореализуемых активов.

В западной практике наибольшее распространение получили модель Баумола (1952 год), модель Миллера-Орра (1966 год) и модель Стоуна (1972 год). Непосредственное применение этих моделей в отечественную практику пока затруднено ввиду сильной инфляции, неразвитости рынка ценных бумаг и т.п., поэтому приведём лишь краткое теоретическое описание данных моделей и их применение на условных примерах.

Модель Баумола

Предполагается, что предприятие начинает работать, имея максимальный и целесообразный для него уровень денежных средств, и затем постоянно расходует их в течение некоторого периода времени. Все поступающие средства от реализации товаров и услуг предприятие вкладывает в краткосрочные ценные бумаги. Как только запас денежных средств истощается, т.е. становится равным нулю или достигает некоторого заданного уровня безопасности, предприятие продаёт часть ценных бумаг и тем самым пополняет запас денежных средств до первоначальной величины. Таким образом, динамика остатка средств на расчётном счёте (ось ОУ) представляет собой «пилообразный» график (рис.2.).

Q

Время

Рис.2. График изменения остатка средств на расчётном счёте (модель Баумола)

Сумма пополнения (Q) вычисляется по формуле:

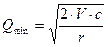, (4)

где V - прогнозируемая потребность в денежных средствах в периоде (год, квартал, месяц);

с - расходы по конвертации денежных средств в ценные бумаги;

r- приемлемый и возможный для предприятия процентный доход по краткосрочным финансовым вложениям, например, в государственные ценные бумаги.

Таким образом, средний запас денежных средств составляет Q/2, а общее количество сделок по конвертации ценных бумаг в денежные средства (k) равно:

k = V/Q (5)

Общие расходы (TC) по реализации такой политики управления денежными средствами составят:

TC=с*k+ r*Q/2 (6)

Первое слагаемое в этой формуле представляет собой прямые расходы, второе - упущенная выгода от хранения средств на расчётном счёте вместо того, чтобы инвестировать их в ценные бумаги.

Дифференцируем последнее уравнение по Q и, приравнивая первую производную к нулю, получим Qmin:

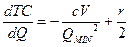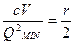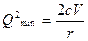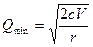, , , . (7)

Пример: Предположим, что денежные расходы компании в течение года составляют 1,5 млн. долл. Процентная ставка по государственным ценным бумагам равна 8%, а затраты, связанные с каждой их реализацией составляют 25 долл. Следовательно, Q = 30,6 тыс. долл.

Q=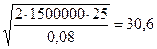

Средний размер денежных средств на расчётном счёте составляет 15,3 тыс. долл. Общее количество сделок по трансформации ценных бумаг в денежные средства за год составит:

1500000долл.:30600долл. = 49.

Таким образом, политика компании по управлению денежными средствами и их эквивалентам такова: как только средства на расчётном счёте истощаются, компания должна продать часть ценных бумаг приблизительно на сумму в 30 тыс. долл.

Такая операция будет выполняться примерно раз в неделю. Максимальный размер денежных средств на расчётном счёте составит 30,6 тыс. долл., средний - 15,3 тыс. долл.