Основное уравнение движения поезда. Вывод уравнения. Учет инерции вращающих частей поезда. Способы решения уравнения.

Из теоретической механики известно, что теорема об изменении кинетической энергии системы гласит: «Изменение кинетической энергии механической системы при некотором ее перемещении равно алгебраической сумме работ внешних и внутренних сил на этом перемещении».

В соответствии с принятыми допущениями работа внутренних сил поезда равна нулю, а сам поезд рассматривается как материальная точка с одной степенью свободы. Следовательно, можно рассматривать только внешние силы, действующие вдоль направления движения поезда. С учетом принятых допущений расчетная схема примет вид, показанный на рисунке 1.

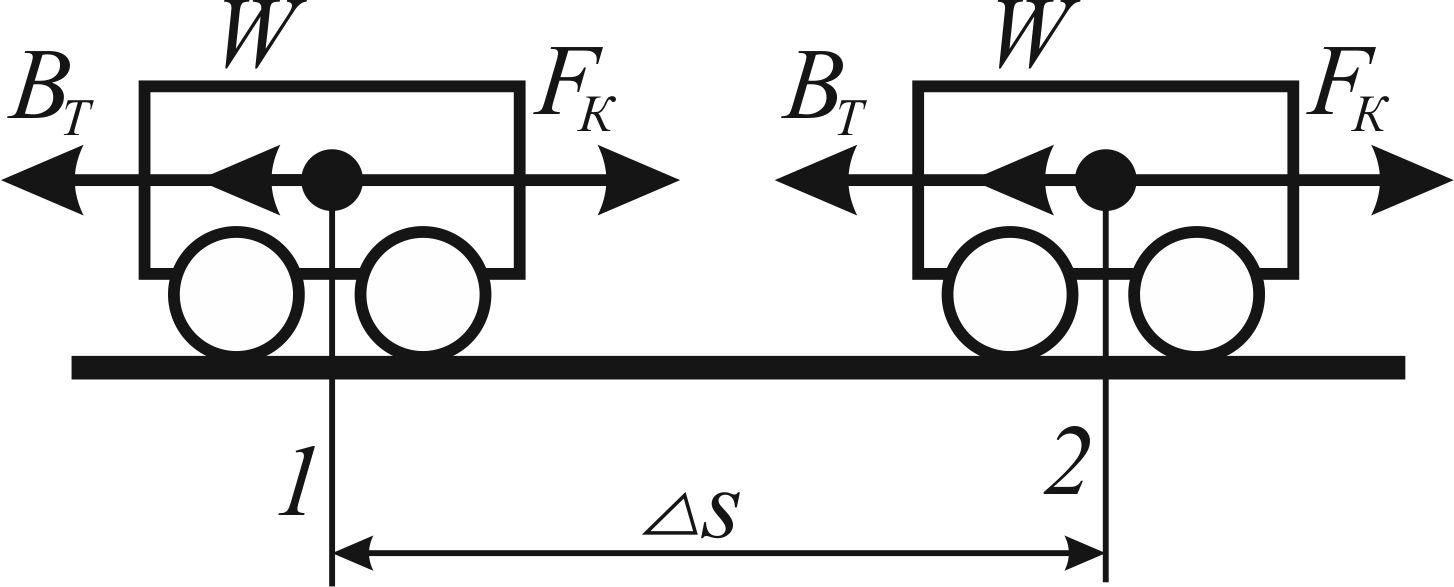
Рисунок 1. Расчетная схема перемещения поезда

1 и 2 – начальное и конечное положения центра масс поезда; Δs – путь, пройденный при перемещении из точки 1 в точку 2.

Математическая интерпретация изложенной выше теоремы имеет вид:

.

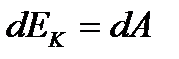Переходя от бесконечно малых величин, к малым получим:

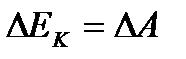
где 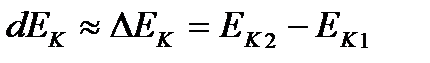- изменение кинетической энергии системы при перемещении центра масс поезда из точки 1 в точку 2 на расчетной схеме;

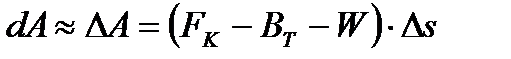- работа, совершаемая силами, действующими на поезд.

В момент перемещения поезда из точки 1 в точку 2, считаем силы действующие на него постоянными и равными их среднему значению за рассматриваемый промежуток времени.

Так как поезд состоит из поступательно движущихся и вращающихся частей, то его кинетическая энергия в каждый момент времени равна:

;

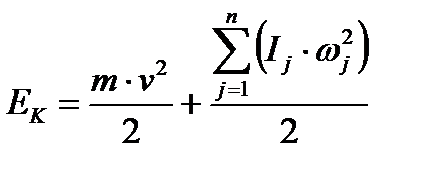где m – масса поезда; v - скорость движения поезда; I_j – момент инерции j –й вращающейся массы поезда; ω_j – угловая скорость вращения j-й вращающейся массы поезда; n - число вращающихся масс в поезде.

Очевидно, что к вращающимся массам поезда относятся следующие элементы:

- колесные пары подвижного состава;

- тяговые двигатели и осевые редукторы локомотивов и самоходного подвижного состава;

- подвагонные генераторы пассажирских вагонов.

Если пренебречь проскальзыванием колесных пар по рельсам в процессе реализации тормозных и тяговых усилий, то их угловые скорости вращения можно выразить через следующее соотношение:

;

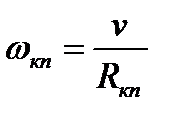где R_кп – радиус колесной пары. Стоит отметить, что радиусы колесных пар различных единиц подвижного состава отличаются.

Угловые скорости вращения тяговых двигателей и подвагонных генераторов могут определены через передаточные отношения приводных механизмов (редукторов, ременных передач и т.п.) и равны:

;

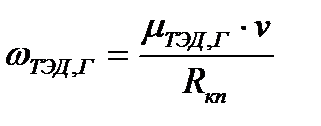где µ - передаточное число приводного механизма.

В общем виде для любой вращающейся массы поезда можно записать:

.

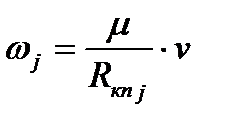При этом передаточное отношение µ для колесной пары принимаем равным 1.

Следовательно, выражение для кинетической энергии поезда можно представить в виде:

.

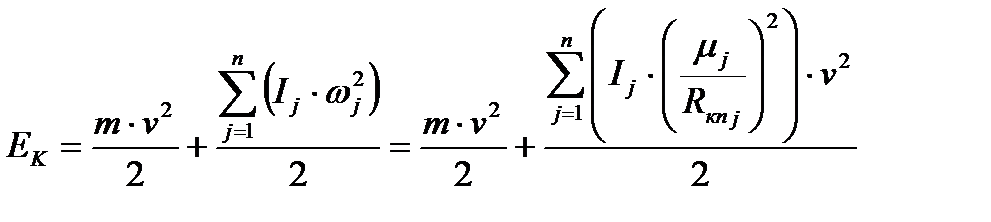Так как моменты инерции, передаточные числа приводных механизмов и радиусы колесных пар подвижного состава в процессе движения поезда, как и его масса практически не изменяются, то в выражении для энергии все составляющие кроме скорости остаются неизменными.

Введем постоянный коэффициент γ, учитывающий долю инерции, составляемую вращающимися массами поезда, и равный:

.

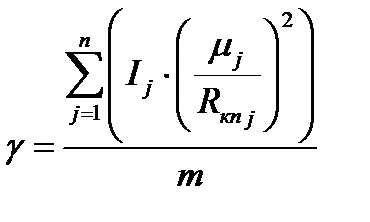Тогда выражение для кинетической энергии поезда можно записать в виде:

.

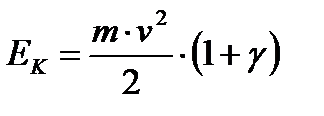Тогда изменение кинетической энергии равно:

.

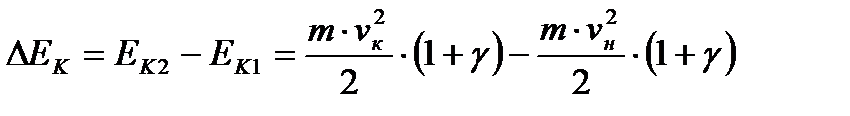Произведя элементарные преобразования, получим:

.

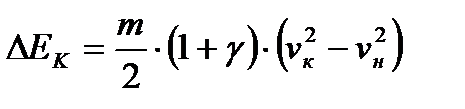Как известно из курса алгебры разность квадратов двух величин равна произведению их суммы на их разность, т.е.

.

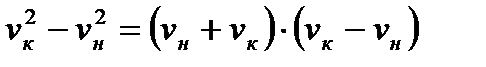Получаем следующее выражение:

.

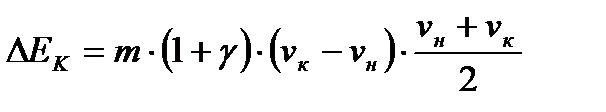Разница между начальной и конечной скоростью представляет собой изменение скорости движения поезда при прохождении им пути Δs. Т.е.

.

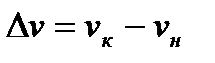Полусумма скоростей движения поезда в начале и конце рассматриваемого участка представляют собой среднюю скорость движения по участку. Т.е.

.

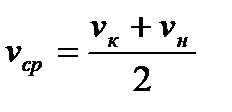Таким образом, изменение кинетической энергии поезда при прохождении рассматриваемого интервала равно:

.

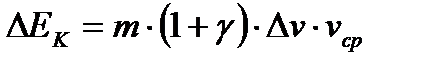С другой стороны средняя скорость на рассматриваемом интервале равна отношению пройденного пути (Δs) к затраченному на этот путь времени (Δt):

.

Приравняв изменение энергии к совершенной работе получим:

.

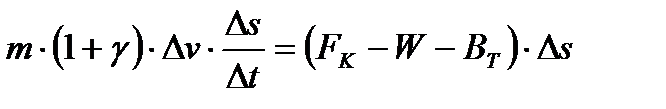Сократив Δs в левой и правой части получим:

.

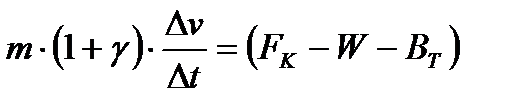После ряда преобразований, уравнение примет вид:

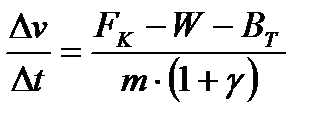
В практике тяговых расчетов, как правило, используются не абсолютные величины сил, действующих на поезд, а их удельные значения, приведенные к весу поезда (P+Q) и рассмотренные нами ранее.

Масса поезда (кг) равна силе его веса (Н), деленного на ускорение свободного падения (9,81 м/с²):

.

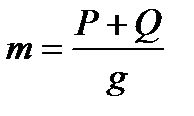Подставив вес поезда в уравнение, получим:

;

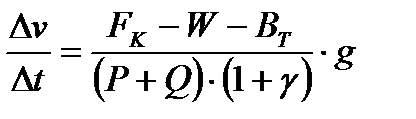или с учетом того, что

; ; ;

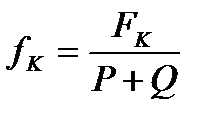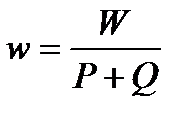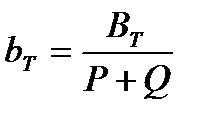введя коэффициент «единичного ускорения»:

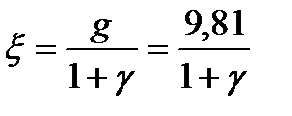(м/с²);

получим:

.

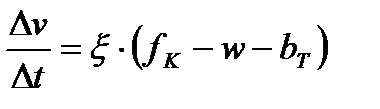Также стоит отметить, что в полученном выражении скорость измеряется в м/с, время в секундах, а удельные силы имеют размерность Н/Н.

В принятой практике тяговых расчетов, закрепленной в ПТР для поездной работы, скорость измеряется в км/ч, ускорение км/ч², а удельные силы измеряются отношением кгс/тс или Н/кН.

Для того чтобы перейти к указанной выше размерности требуется в выражении для единичного ускорения ξ ускорение свободного падения g перевести из м/с² в км/ч², а также разделить его на 1000 чтобы значение знаменателя для удельных сил представлять в тс при числителе кгс или в кН при числителе Н.

Перевод из м/с² в км/ч² осуществляется умножением на 3600² (секунды в квадрате переводим в часы в квадрате) и делением на 1000 (км переводим в м). С учетом дополнительного деления на 1000 для получения удобной размерности удельных сил получим следующее значение «единичного ускорения»:

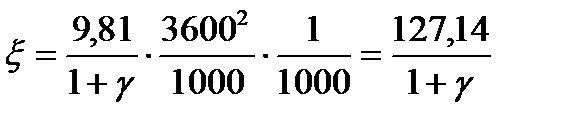(км/ч²/1000).

При переходе к данному значению «единичного ускорения» основное уравнение движения поезда не изменится.

Коэффициент инерции вращающихся частей поезда γ.

Одним из наиболее сложных вопросов в решении основного уравнения движения поезда является правильное определение коэффициента, учитывающего долю инерции вращающих масс поезда.

Как было записано ранее в общем виде выражение имеет вид:

.

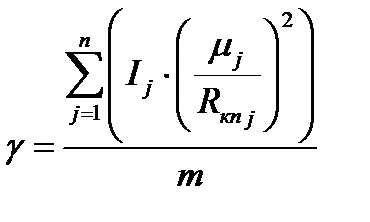Если рассматривать один грузовой вагон, то для него выражение примет вид:

;

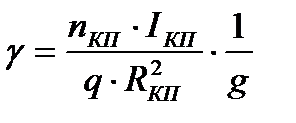где n_КП - число колесных пар у вагона; I_КП – момент инерции колесной пары относительно ее оси вращения; q – вес вагона, тс; R_КП – радиус колесной пары по кругу катания; g=9,81м/с² – ускорение свободного падения. Известно, что для стандартной колесной пары грузового вагона момент инерции составляет 1300 Нм² (не совпадает с 420 кгс), соотношение 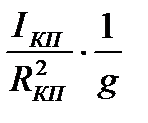составляет 420 кгс.

Как видно из выражения коэффициент во многом зависит от загрузки вагона и может колебаться в довольно широких пределах от 0,02 у полностью загруженного вагона до 0,08 у порожнего вагона. У пассажирских вагонов коэффициент составляет порядка 0,04. Для локомотивов коэффициент инерции вращающихся масс, как правило, значительно выше из-за наличия тяговых двигателей и осевых редукторов и составляет от 0,11 у пассажирских до 0,24 у грузовых локомотивов.

Когда состав состоит из разнотипных вагонов, то доля инерции вращающихся масс для него может быть определена по зависимости:

;

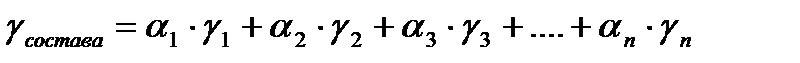где α₁-α_n –доля вагонов данного типа по весу состава; γ₁-γ_n – коэффициент инерции вращающихся частей вагона данного типа.

Для грузового поезда, состоящего из вагонов с разным числом осей принято следующее выражение:

;

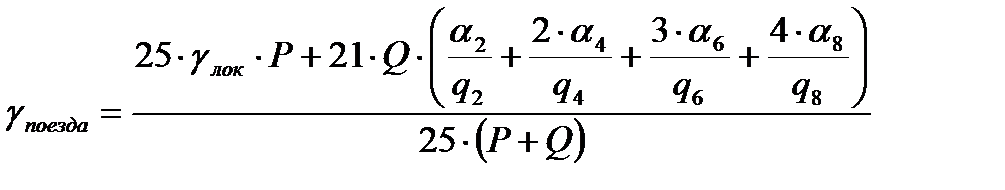где α₂, α₄, α₆, α₈ – доля соответственно 2-х, 4-х, 6-ти и 8-ми осных вагонов по весу в составе; q₂, q₄, q₆, q₈ – вес соответственно 2-х, 4-х, 6-ти и 8-ми осных вагонов.