Решение уравнения движения по интервалам скорости.

Полученное ранее основное уравнение движения поезда трансформируем следующим образом:

Время за интервал равняется пройденному пути деленному на среднюю скорость движения:

.

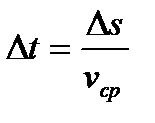Тогда 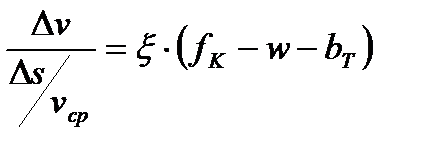или

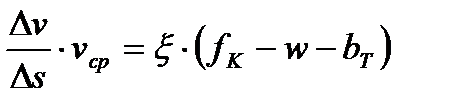
Выполняем обратные от выполненных ранее преобразований для левой части уравнения:

;

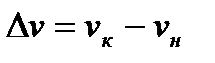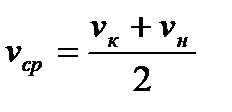; получим

.

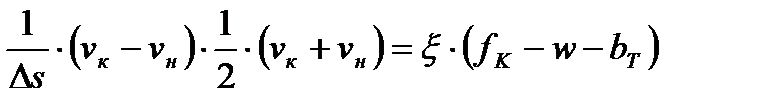Вспоминая, что 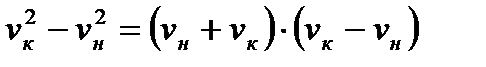получим

.

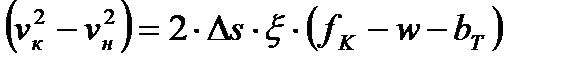Выражая из соотношения пройденный путь придем к выражению:

.

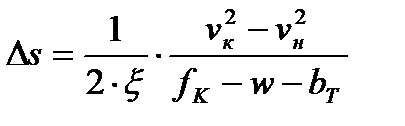В приведенном виде пройденный путь выражен в км. Чтобы получить результат в м, правую часть необходимо умножить на 1000. Тогда выражение примет вид.

.

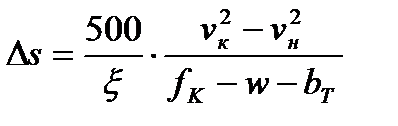При использовании данного метода построения кривой скорости используется следующий порядок.

- задаемся изменением скорости движения с шагом не более 10км/ч;

- по средней между начальной и конечной скоростью определяем удельные силы действующие на поезд;

- вычисляем пройденный путь.

- если полученный пройденный путь нас по каким-то причинам не устраивает изменяем интервал скорости;

- если интервал пройденного пути получился отрицательным, то это говорит о том, что характер изменения скорости задан неверно (поезд не разгоняется, а замедляется и наоборот);

- если интервал пройденного пути близок или равен бесконечности это говорит о том, что скорость в рассматриваемых условиях не изменяется.