Спектры периодических сигналов.

Периодическими называют сигналы, обладающие следующим свойством:

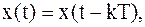
	(1)
где	T	–	период;
	k = 0, 1, 2, 3 …

Как известно из курса высшей математики, такие функции, удовлетворяющие условиям Дирихле, можно описать суммой тригонометрического ряда (ряда Фурье):

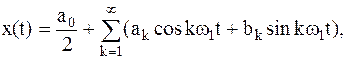
	(2)
где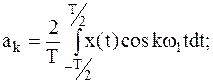

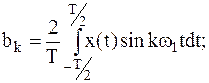
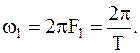
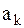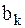Формула (2) ряда Фурье удобна с точки зрения простоты вычисления коэффициентов разложения и . Ряд Фурье можно записать иначе:

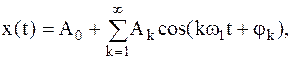
	(3)
где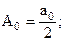

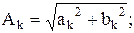
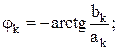
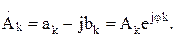
Совокупность амплитуд 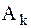называют амплитудным, а совокупность фаз 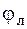– фазовымспектрами. Их можно изображать графически (рис. 1).

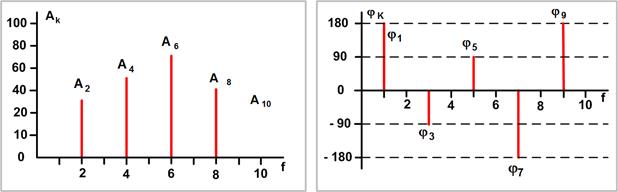
Рисунок 1 – Амплитудный и фазовый спектры

Амплитудный и фазовый спектры сигнала в совокупности определяют его форму (временную зависимость).

Наиболее компактной является запись ряда Фурье в комплексной форме:

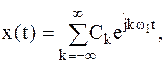
	(4)
где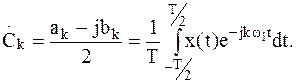

Комплексный спектр (4) можно интерпретировать как представление 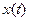в виде сумм спектральных составляющих 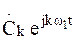, каждая из которых представляет пару гармонических колебаний с половинной амплитудой 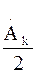на положительной 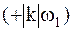и отрицательной 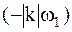частотах. Для вещественных функций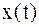 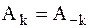– амплитудный спектр – чётная функция частоты, 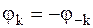– фазовый спектр – нечётная функция частоты.

Ряд Фурье является частным случаем обобщённого ряда Фурье при выборе в качестве базиса совокупности тригонометрических 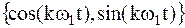или экспоненциальных 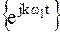функций.

Выводы

1. Математическим аппаратом спектрального анализа периодических сигналов является ряд Фурье.

2. Спектры периодических сигналов дискретные (линейчатые), представляют совокупность амплитуд и фаз гармонических колебаний.