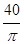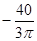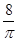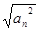Глава 4. Спектральное представление периодических сигналов
| Электрические сигналы, математическими моделями которых являются периодические функции времени, могут быть представлены в виде графического описания (рис. 6) и соответствующего ему аналитического представления. Любое периодическое несинусоидальное колебание можно разложить в бесконечный тригонометрический ряд, состоящий из постоянной составляющей и гармонических составляющих. | 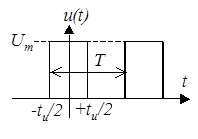
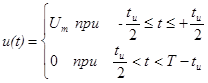
|
| Рис. 6 |
Тригонометрический ряд, называемый еще рядом Фурье (24), имеет две формы записи.
В первой форме, кроме постоянной составляющей, присутствуют лишь синусоидальные или косинусоидальные составляющие с начальными фазами, не равными нулю:
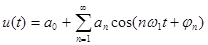 . (25)
. (25)
Во второй форме наряду с постоянной составляющей присутствуют синусоидальные и косинусоидальные составляющие, но с начальными фазами, равными нулю:
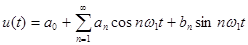 . (26)
. (26)
В обеих формах записи использованы следующие обозначения: 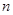 – номер гармоники;
– номер гармоники; 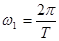 – круговая частота первой (основной) гармоники;
– круговая частота первой (основной) гармоники; 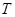 – период колебания;
– период колебания; 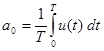 – постоянная составляющая;
– постоянная составляющая; 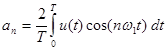 – амплитуда
– амплитуда 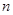 –й косинусоидальной составляющей;
–й косинусоидальной составляющей;  – амплитуда
– амплитуда 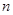 –й синусоидальной составляющей.
–й синусоидальной составляющей.
| Графическое изображение ряда Фурье (рис. 7) представляет собой спектральную диаграмму, которая дает наглядное представление о зависимости амплитуд гармоник (спектр амплитуд) и фаз гармоник (спектр фаз) от их частот. | Спектр амплитуд
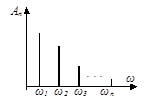
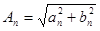
| Спектр фаз
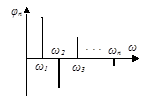
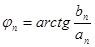
|
| Рис. 7 |
Ряд Фурье существенно упрощается, если имеет место какая–либо симметрия колебания относительно начала или осей координат. В табл. 2 приведены соответствующие упрощения.
| Табл. 2 | |||
| Кривая симметрична относительно: | |||
| 1) | оси ординат (четная функция): 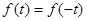 . .
| ||
| 2) | начала координат (нечетная функция): 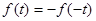 . .
| ||
| 3) | оси абсцисс при совмещении двух полупериодов: 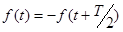 . .
| ||
| 4) | оси ординат и оси абсцисс при совмещении полупериодов: 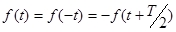 . .
| ||
| 5) | начала координат и оси абсцисс при совмещении двух полупериодов: 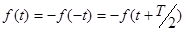 . .
|
Спектральная диаграмма (спектр) зависит от формы сигналов и их параметров. Пусть, например, необходимо построить спектральную диаграмму сигнала, графическое и аналитическое представление которого приведено на рис. 8. Параметры сигнала приведены рядом.
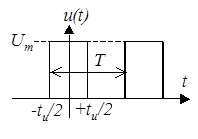
| 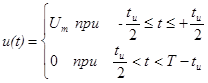
| 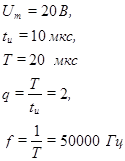
|
| Рис. 8 |
Из сопоставления графического представления сигнала (рис. 8) с табл. 2 можно сделать вывод о том, что описывающая сигнал функция является четной, следовательно, в спектре сигнала отсутствуют синусоидальные ( 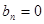 ) составляющие. Постоянная составляющая в соответствии с приведенным ранее выражением находится следующим образом:
) составляющие. Постоянная составляющая в соответствии с приведенным ранее выражением находится следующим образом:
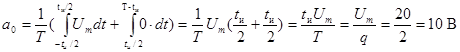 .
.
Амплитуды гармоник:
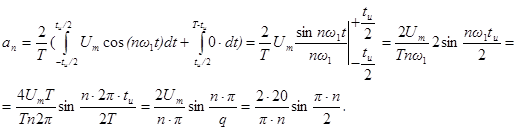
Таким образом, разложение данной функции в ряд Фурье может быть представлено следующим образом:
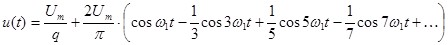 .
.
Из этого выражения можно сделать вывод о том, что амплитуды четных гармоник в спектре данного сигнала равны нулю 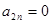 . Остальные расчеты сведены в табл. 3., используя которую можно построить спектральную диаграмму данного сигнала (рис. 9).
. Остальные расчеты сведены в табл. 3., используя которую можно построить спектральную диаграмму данного сигнала (рис. 9).
| 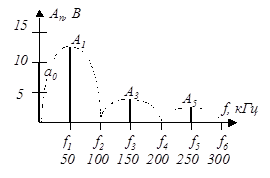
| |||||||||||||||||||||||||||||
| Рис. 9 |
Эти же расчеты позволяют записать аналитическое представление разложения рассматриваемого сигнала в ряд Фурье с конкретными числовыми коэффициентами
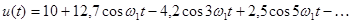 ,
,
где
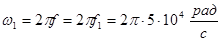 .
.
Из приведенного примера можно сделать следующие выводы:
1. Спектр периодической последовательности является дискретным, линейчатым.
2. Количество спектральных линий в одном лепестке огибающей спектра определяется скважностью, так как интервал между спектральными линиями обратно пропорционален периоду, а точки пересечения огибающей спектра с осью частот определяются в данном случае длительностью импульса ( 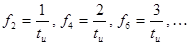 ).
).
Спектральное разложение периодического сигнала можно выполнить и несколько по иному, используя систему базисных функций, состоящую из экспонент с мнимыми показателями:
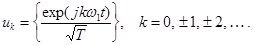 (27)
(27)
Функции этой системы периодичны с периодом 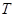 и ортонормированы на отрезке времени
и ортонормированы на отрезке времени 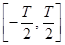 , так как
, так как
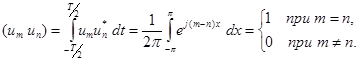
Функции из рассматриваемой системы принимают комплексные значения. Поэтому при вычислении скалярного произведения используется операция комплексного сопряжения ( 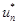 ).
).
Ряд Фурье произвольного периодического сигнала 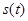 в данном случае принимает вид:
в данном случае принимает вид:
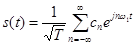 с коэффициентами
с коэффициентами 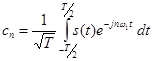 .
.
Обычно используют следующую форму записи:
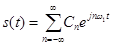 , (28)
, (28)
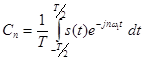 . (29)
. (29)
Выражение (28) представляет собой ряд Фурье в комплексной форме. Спектр сигнала в соответствии с формулой (28) содержит компоненты на отрицательной полуоси частот, причем 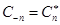 . В ряде (28) слагаемые с положительными и отрицательными частотами объединяются в пары, например:
. В ряде (28) слагаемые с положительными и отрицательными частотами объединяются в пары, например:
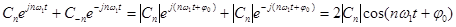 .
.
Положительной частоте соответствует вектор, вращающийся против часовой стрелки, а отрицательной частоте – вектор, вращающийся по часовой стрелке. Итак, отрицательная частота – понятие не физическое, а математическое, вытекающее из способа представления комплексных чисел.
Структура ряда Фурье (28) дает возможность изобразить периодический сигнал посредством бесконечной суммы вращающихся векторов на комплексной плоскости.
Дата добавления: 2016-09-06; просмотров: 3099;

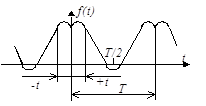
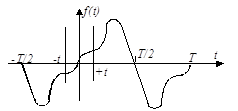
 );
);
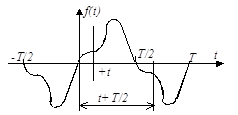
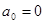 ) и четные синусоидальные и косинусоидальные составляющие (
) и четные синусоидальные и косинусоидальные составляющие ( 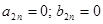 );
);
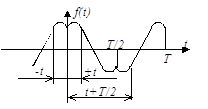
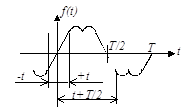
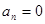 ) и четные синусоидальные составляющие (
) и четные синусоидальные составляющие ( 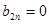 ).
).
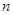
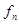 , кГц
, кГц