Спектры Т – финитных сигналов

Т – финитными называют ограниченные по времени сигналы. По определению они не могут быть периодическими и, следовательно, к ним не применимо разложение в ряд Фурье.

Для описания таких сигналов применим приём:

На первом этапе от заданного сигнала х(t), имеющего начало в точке 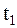и конец в точке 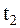, переходим к сигналу 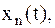который является периодическим повторением х(t) на бесконечной оси времени с периодом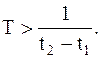

Данный сигнал можно разложить в ряд Фурье:

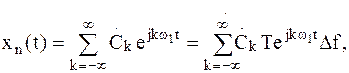
	(5)
где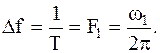

Для описания спектра финитного сигнала приходим к известному в математике интегральному преобразованию Фурье:

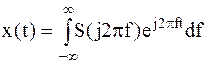– прямое преобразование,

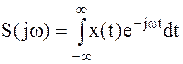– обратное преобразование.

Из полученных соотношений следует, что спектр Т-финитного сигнала сплошной. Он представляет собой совокупность бесконечного числа составляющих с бесконечно малыми амплитудами, непрерывно следующих по оси частот.

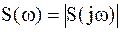– амплитудный спектр,

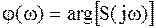– фазовый спектр

Выводы

1. Математическим аппаратом спектрального анализа Т – финитных сигналов является интегральное преобразование Фурье.

2. Спектры Т – финитных сигналов сплошные и описываются непрерывными функциями частоты в виде модуля спектральной плотности амплитуд 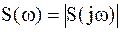(амплитудный спектр) и ее аргумента 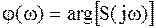(фазовый спектр).