Глава 5. Спектральное представление непериодических сигналов
Метод рядов Фурье допускает обобщение, позволяющее получать спектральные характеристики непериодических сигналов. Среди них наибольший интерес представляют импульсные сигналы.
Если предположить, что период последовательности прямоугольных импульсов T®µ , то получим спектр одиночного прямоугольного импульса, т. е. непериодического сигнала.
Математически спектр непериодической функции определится уже не рядом Фурье, а интегралом Фурье, он будет не дискретным, а сплошным, и будет называться спектральной плотностью или спектральной характеристикой, или Фурье–образом сигнала
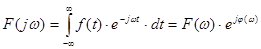 . (30)
. (30)
Полученное выражение, обеспечивающее переход от представления сигнала во временной области к его представлению в частотной области, называется прямым преобразованием Фурье. Если известно представление сигнала в частотной области 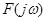 , то можно найти его представление во временной области за счет использования обратного преобразования Фурье:
, то можно найти его представление во временной области за счет использования обратного преобразования Фурье:
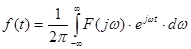 .
.
Спектральная плотность одиночного прямоугольного импульса, вычисленная с помощью интеграла Фурье, имеет следующий вид (рис. 10): 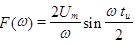 , где , где 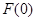 равно вольт-секундной площади сигнала, в данном случае равно вольт-секундной площади сигнала, в данном случае 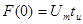 . .
| 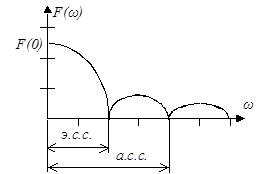
|
| Рис. 10 |
Из сопоставления закона изменения амплитуд гармонических составляющих дискретного спектра периодической последовательности прямоугольных импульсов и формы кривой спектральной плотности одиночного прямоугольного импульса можно сделать важный и общий для всех форм импульсов вывод: дискретный спектр периодической последовательности импульсов вписывается в кривую спектральной плотности одиночного импульса этой же формы, которая называется огибающей дискретного спектра.
Ширину первого лепестка (90 % энергии сигнала) спектральной диаграммы принято называть энергетическим спектром сигнала (э.с.с.). Ширину двух лепестков (95 % энергии сигнала) – активным спектром сигнала (а.с.с.).
Ограниченный диапазон частот, в котором располагается энергетический спектр сигнала или активный спектр сигнала называется шириной спектра сигнала.
Устройства, которые работают с сигналом, должны иметь более широкий рабочий диапазон частот (полосу пропускания), чем ширина спектра сигнала.
Плотность спектра – количество спектральных линий на одном лепестке – определяется соотношением между длительностью импульса и периодом, интервал между спектральными линиями обратно пропорционален периоду.
Если сигнал описывается функцией вида 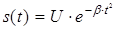 , то он называется гауссовым импульсом. Такой сигнал лишь условно можно назвать импульсом из-за его поведения при
, то он называется гауссовым импульсом. Такой сигнал лишь условно можно назвать импульсом из-за его поведения при 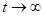 . Однако, условие
. Однако, условие 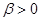 обеспечивает достаточно быстрое уменьшение мгновенного значения сигнала с ростом времени. Поэтому применяют понятие эффективной длительности подобных импульсов, определяемое из условия десятикратного уменьшения уровня сигнала, т.е.
обеспечивает достаточно быстрое уменьшение мгновенного значения сигнала с ростом времени. Поэтому применяют понятие эффективной длительности подобных импульсов, определяемое из условия десятикратного уменьшения уровня сигнала, т.е. 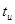 находится из условия
находится из условия 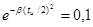 . С учетом этого спектральная плотность гауссова импульса
. С учетом этого спектральная плотность гауссова импульса 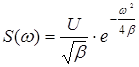 . Таким образом, спектральная плотность гауссова импульса вещественна и описывается гауссовой же функцией частоты.
. Таким образом, спектральная плотность гауссова импульса вещественна и описывается гауссовой же функцией частоты.
Еще одним важным примером непериодических сигналов является так называемый экспоненциальный импульс, описываемый функцией 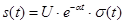 . Такой сигнал, как и гауссов импульс, лишь условно можно назвать импульсом из-за его поведения при
. Такой сигнал, как и гауссов импульс, лишь условно можно назвать импульсом из-за его поведения при 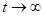 . Однако, условие
. Однако, условие 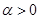 обеспечивает достаточно быстрое (экспоненциальное) уменьшение мгновенного значения сигнала с ростом времени. Эффективную длительность такого импульса определяют аналогично из условия десятикратного уменьшения уровня сигнала
обеспечивает достаточно быстрое (экспоненциальное) уменьшение мгновенного значения сигнала с ростом времени. Эффективную длительность такого импульса определяют аналогично из условия десятикратного уменьшения уровня сигнала 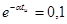 , откуда
, откуда 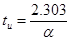 . Спектральная плотность экспоненциального импульса
. Спектральная плотность экспоненциального импульса 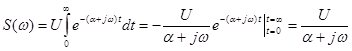 . Можно отметить принципиальные особенности, отличающие спектральную плотность экспоненциального импульса от спектра импульса прямоугольной формы:
. Можно отметить принципиальные особенности, отличающие спектральную плотность экспоненциального импульса от спектра импульса прямоугольной формы:
1. Спектральная плотность экспоненциального импульса не обращается в нуль ни при каком конечном значении частоты.
2. Спектральная плотность экспоненциального импульса есть комплексная функция 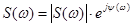 , имеющая модуль (амплитудный спектр)
, имеющая модуль (амплитудный спектр) 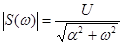 и аргумент (фазовый спектр)
и аргумент (фазовый спектр) 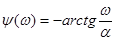 .
.
Пусть сигнал 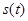 представляет собой короткий импульс, сосредоточенный в точке
представляет собой короткий импульс, сосредоточенный в точке 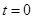 и имеющий площадь
и имеющий площадь 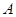 . Его математическая модель
. Его математическая модель 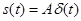 , где
, где 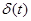 – дельта - функция. Спектральная плотность этого сигнала
– дельта - функция. Спектральная плотность этого сигнала 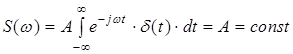 , т.е. дельта - импульс имеет равномерный спектр на всех частотах.
, т.е. дельта - импульс имеет равномерный спектр на всех частотах.
Если ввести понятие ширины спектра сигнала и понимать под ней частотный интервал, в пределах которого модуль спектральной плотности не меньше некоторого наперед заданного уровня, например (рис. 11), изменяется в пределах от 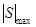 до до 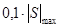 , ,
| 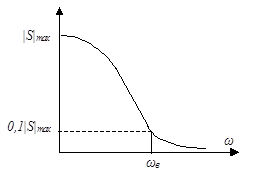
|
| Рис. 11 |
то из рассмотренных примеров можно заключить, что 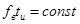 , откуда следует важный вывод: чем меньше длительность импульса, тем шире его спектр.
, откуда следует важный вывод: чем меньше длительность импульса, тем шире его спектр.
Обобщая сказанное о спектральном представлении сигналов, можно сделать следующие выводы:
1. Спектральное представление сигнала представляет собой разложение его на сумму (конечную или бесконечную) элементарных гармонических процессов с различными частотами.
2. Периодические сигналы представляются в виде рядов Фурье, которые образуются суммированием бесконечного числа гармоник с частотами, кратными основной частоте периодического процесса.
3. Спектральное представление непериодических, в частности импульсных, сигналов осуществляется путем их разложения в интеграл Фурье.
4. В частотной области непериодический сигнал характеризуется своей спектральной плотностью. Сигнал и его спектр взаимно связаны парой прямого и обратного преобразований Фурье.
5. Для существования спектральной плотности в классическом смысле необходимо, чтобы функция, описывающая процесс, была абсолютно интегрируема.
6. Спектральная плотность неинтегрируемой функции содержит особенности типа дельта – функции
Еще один вид интегральных преобразований, который наряду с преобразованием Фурье широко используется для решения самых разнообразных задач, связанных с изучением сигналов, называется преобразованием Лапласа.
Спектральные методы основаны на том, что исследуемый сигнал представляется в виде суммы неограниченно большого числа элементарных слагаемых, каждое из которых периодически изменяется во времени по закону 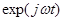 .
.
Естественное обобщение этого принципа заключено в том, что вместо комплексных экспоненциальных сигналов с чисто мнимыми показателями вводят в рассмотрение экспоненциальные сигналы вида 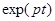 , где
, где 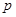 – комплексное число:
– комплексное число: 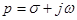 , получившее название комплексной частоты.
, получившее название комплексной частоты.
Из двух таких комплексных сигналов можно составить вещественный сигнал, например, по следующему правилу:
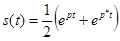 , (31)
, (31)
где 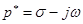 – комплексно-сопряженная величина.
– комплексно-сопряженная величина.
Действительно, при этом
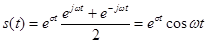 . (32)
. (32)
В зависимости от выбора вещественной и мнимой частей комплексной частоты можно получить разнообразные вещественные сигналы. Так, если 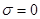 , но
, но 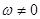 , получаются обычные гармонические колебания вида
, получаются обычные гармонические колебания вида 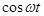 . Если же
. Если же 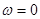 , то в зависимости от знака
, то в зависимости от знака 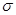 получаются либо нарастающие, либо убывающие во времени экспоненциальные колебания. Более сложную форму такие сигналы приобретают, когда
получаются либо нарастающие, либо убывающие во времени экспоненциальные колебания. Более сложную форму такие сигналы приобретают, когда 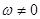 . Здесь, множитель
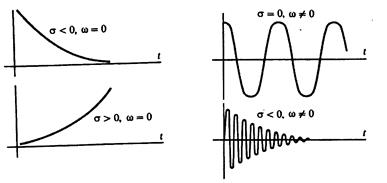
. Здесь, множитель 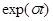 описывает огибающую, которая экспоненциально изменяется во времени. Некоторые типичные сигналы изображены на рис. 12.
описывает огибающую, которая экспоненциально изменяется во времени. Некоторые типичные сигналы изображены на рис. 12.
|
| Рис. 12 |
Понятие комплексной частоты оказывается весьма полезным прежде всего потому, что это дает возможность получать спектральные представления сигналов, математические модели которых неинтегрируемы.
Следует обратить внимание на то, что истинная физическая частота 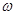 служит мнимой частью комплексной частоты. Для вещественной части
служит мнимой частью комплексной частоты. Для вещественной части 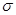 комплексной частоты специального термина не существует.
комплексной частоты специального термина не существует.
Пусть 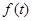 – некоторый сигнал, вещественный или комплексный, определенный при
– некоторый сигнал, вещественный или комплексный, определенный при 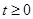 и равный нулю при отрицательных значениях времени. Преобразование Лапласа этого сигнала есть функция комплексной переменной
и равный нулю при отрицательных значениях времени. Преобразование Лапласа этого сигнала есть функция комплексной переменной 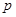 , задаваемая интегралом:
, задаваемая интегралом:
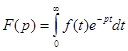 . (33)
. (33)
Сигнал 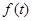 называется оригиналом, а функция
называется оригиналом, а функция 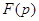 – его изображением по Лапласу (для краткости, просто изображением).
– его изображением по Лапласу (для краткости, просто изображением).
Условие, которое обеспечивает существование интеграла (33), заключается в следующем: сигнал 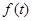 должен иметь не более чем экспоненциальную степень роста при
должен иметь не более чем экспоненциальную степень роста при 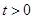 , т. е. должен удовлетворять неравенству
, т. е. должен удовлетворять неравенству 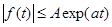 , где
, где 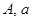 – положительные числа.
– положительные числа.
При выполнении этого неравенства функция 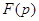 существует в том смысле, что интеграл (33) абсолютно сходится для всех комплексных чисел
существует в том смысле, что интеграл (33) абсолютно сходится для всех комплексных чисел 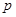 , у которых
, у которых 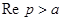 . Число
. Число 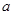 называют абсциссой абсолютной сходимости.
называют абсциссой абсолютной сходимости.
Переменная 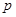 в формуле (33) может быть отождествлена с комплексной частотой
в формуле (33) может быть отождествлена с комплексной частотой 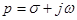 . Действительно, при чисто мнимой комплексной частоте, когда
. Действительно, при чисто мнимой комплексной частоте, когда 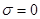 , формула (32) переходит в формулу (30), определяющую Фурье-преобразование сигнала, который равен нулю при
, формула (32) переходит в формулу (30), определяющую Фурье-преобразование сигнала, который равен нулю при 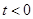 .
.
Таким образом, преобразование Лапласа можно рассматривать как обобщение преобразования Фурье на случай комплексных частот.
Подобно тому, как это делается в теории преобразования Фурье, можно, зная изображение, восстановить оригинал. Для этого в формуле обратного преобразования Фурье
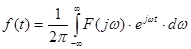
следует выполнить аналитическое продолжение, перейдя от мнимой переменной 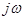 к комплексному аргументу
к комплексному аргументу 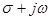 .
.
На плоскости комплексной частоты интегрирование проводят вдоль неограниченно протяженной вертикальной оси, расположенной правее абсциссы абсолютной сходимости. Поскольку при 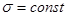 дифференциал
дифференциал 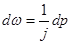 , формула обратного преобразования Лапласа приобретает вид
, формула обратного преобразования Лапласа приобретает вид
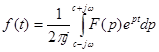 . (34)
. (34)
или 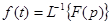 , где
, где 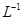 – символ обратного преобразования Лапласа.
– символ обратного преобразования Лапласа.
Отметим, что преобразование Лапласа изображает исходную функцию лишь при 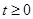 , а поведение исходной функции при
, а поведение исходной функции при 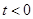 никак не сказывается на изображении. Класс функций, преобразуемых по Лапласу, значительно шире класса функций, преобразуемых по Фурье. Практически любые функции времени имеют преобразование Лапласа.
никак не сказывается на изображении. Класс функций, преобразуемых по Лапласу, значительно шире класса функций, преобразуемых по Фурье. Практически любые функции времени имеют преобразование Лапласа.
Получим, например, изображения по Лапласу для импульсных функций.
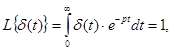
так как 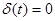 при
при 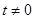 ,
, 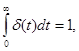 и
и 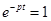 при
при 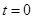 .
.
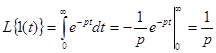 .
.
На практике для выполнения прямого и обратного преобразований Лапласа используются таблицы преобразований, фрагмент одной из которых приведен в табл. 4.
| Табл. 4 | |||||||
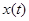
| 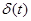
| 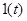
| 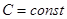
| 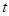
| 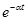
| 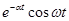
| 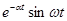
|
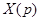
| 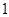
| 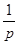
| 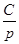
| 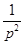
| 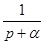
| 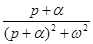
| 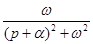
|
Таблицы преобразования Лапласа могут быть использованы для определения Фурье–изображений таких абсолютно интегрируемых функций, которые равны 0 при 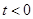 .
.
Рассмотрим формулировки основных теорем преобразования Лапласа.
1. Теорема линейности. Любое линейное соотношение между функциями времени справедливо и для изображений по Лапласу этих функций:
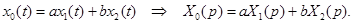
2. Теорема о дифференцировании оригинала. Если 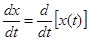
и 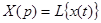 , то
, то 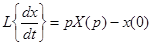 , где
, где 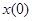 – начальное значение оригинала.
– начальное значение оригинала.
Для второй производной используют выражение
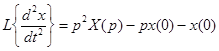 .
.
Для производной 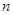 -го порядка справедливо следующее соотношение:
-го порядка справедливо следующее соотношение:
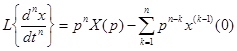 .
.
Для производной 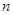 -го порядка при нулевых начальных условиях справедливо следующее соотношение:
-го порядка при нулевых начальных условиях справедливо следующее соотношение:
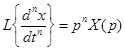 ,
,
то есть дифференцирование 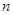 -й степени оригинала по времени при нулевых начальных условиях соответствует умножению изображения на
-й степени оригинала по времени при нулевых начальных условиях соответствует умножению изображения на 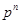 .
.
3. Теорема об интегрировании оригинала.
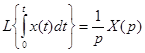 .
.
Таким образом, в области изображений по Лапласу сложные операции дифференцирования и интегрирования сводятся к операциям умножения и деления на 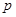 , что позволяет переходить от дифференциальных и интегральных уравнений к алгебраическим. Это является главным достоинством преобразования Лапласа как математического аппарата теории систем.
, что позволяет переходить от дифференциальных и интегральных уравнений к алгебраическим. Это является главным достоинством преобразования Лапласа как математического аппарата теории систем.
4. Теорема запаздывания. Для любого 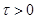 справедливо соотношение
справедливо соотношение
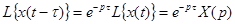 .
.
5. Теорема о свертке (умножении изображений)
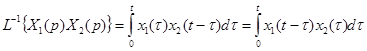 ,
,
где 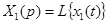 и
и 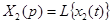 .
.
6. Теорема о предельных значениях. Если 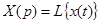 , то
, то
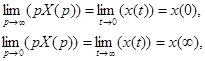
если 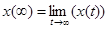 существует.
существует.
Для нахождения оригинала функции по ее изображению используют обратное преобразование Лапласа. Функцию изображения необходимо представить в форме Хэвисайда, воспользовавшись необходимой формулой разложения дробно-рациональной функции. Полученную сумму простейших дробей подвергают обратному преобразованию Лапласа. Для этого можно воспользоваться таблицами преобразования Лапласа, которые определяют изображения многих временных функций.
Контрольные вопросы к лекции 9
9-1. Приведите выражение для разложения периодической функции в тригонометрический ряд Фурье
9-2. Как называется графическое изображение разложения периодической функции в тригонометрический ряд Фурье?
9-3. Что называется спектром амплитуд при разложении периодической функции в тригонометрический ряд Фурье?
9-4. Что называется спектром фаз при разложении периодической функции в тригонометрический ряд Фурье?
9-5. Какие составляющие отсутствуют в спектре при разложении периодической функции, если функция симметрична относительно оси ординат?
9-6. Какие составляющие отсутствуют в спектре при разложении периодической функции, если функция симметрична относительно начала координат?
9-7. Какие составляющие отсутствуют в спектре при разложении периодической функции, если функция симметрична относительно оси абсцисс при совмещении двух полупериодов?
9-8. Какие составляющие отсутствуют в спектре при разложении периодической функции, если функция симметрична относительно оси ординат и оси абсцисс при совмещении полупериодов?
9-9. Какие составляющие отсутствуют в спектре при разложении периодической функции, если функция симметрична относительно начала координат и оси абсцисс при совмещении двух полупериодов?
9-10. Чем определяется количество спектральных линий в одном лепестке огибающей спектра?
9-11. Как записывается ряд Фурье в комплексной форме?
9-12. Что собой представляет отрицательная частота при разложении в ряд Фурье в комплексной форме?
9-13. В чем состоит принципиальное отличие спектра непериодической функции от спектра периодической функции?
9-14. Как связаны дискретный спектр периодической последовательности импульсов и кривая спектральной плотности одиночного импульса этой же формы?
9-15. Что называется энергетическим спектром сигнала?
9-16. Что называется активным спектром сигнала?
9-17. Как связаны длительность импульса и ширина его спектра?
9-18. Запишите выражение для прямого преобразования Лапласа.
9-19. Запишите выражение для обратного преобразования Лапласа.
9-20. В чем состоит суть теоремы линейности для преобразования Лапласа?
9-21. В чем состоит суть теоремы о дифференцировании оригинала для преобразования Лапласа?
9-22. В чем состоит суть теоремы об интегрировании оригинала для преобразования Лапласа?
9-23. В чем состоит суть теоремы запаздывания для преобразования Лапласа?
9-24. В чем состоит суть теоремы о свертке для преобразования Лапласа?
9-25. В чем состоит суть теоремы о предельных значениях для преобразования Лапласа?
Дата добавления: 2016-09-06; просмотров: 3898;











