Изучение погрешностей оптических систем.
Главная задача оптической системы состоит в получении правильного предмета. Так, например, точечный объект с достаточной степенью точности дает точечное изображение, если рассматриваем пучок параксиальных лучей, т.е. лучей, составляющих малые углы с оптической осью. Однако малым значениям углов j соответствуют световые пучки, заключенные в пределах телесных углов. А узость световых пучков ведет к тому, что освещенности в пределах изображения малы. Поэтому с практической точки зрения удобно пользоваться широкими пучками, т.е. отказываться от параксиальных пучков световых лучей. Но в результате этого изображение объекта приобретает ряд недостатков.
1. Сферическая аберрация.
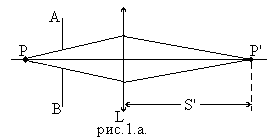 |
Возьмем плосковыпуклую линзу L /рис.1(а)/. С помощью непрозрачного экрана АВ с круглым отверстием /круглой диафрагмы/ выделим от точечного источника Р параксиальный пучок лучей. Пусть он пересекается в точке Р’ на расстоянии S’ от линзы.
Заменим теперь круглую диафрагму диафрагмой с кольцевым отверстием CDEN /рис.1(б)/.
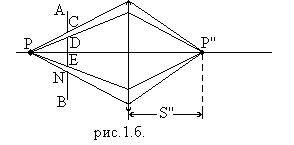 |
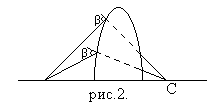
Эта диафрагма выделит из точечного источника Р’ пучок краевых лучей, заключенных между конусами CPD и NPE. Краевые лучи падают на линзу под большим углом a и, следовательно, сильнее преломляются в линзе /рис.2/. При прежнем положении источника S его изображение Р’’ окажется от линзы на расстоянии меньшем S’. Расстояние
dS=S’’ – S’ (*)
 |
называется продольной сферической аберрацией.
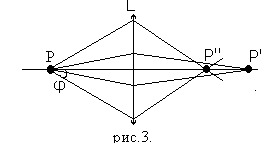 |
Наличие продольной сферической аберрации ведет к размытию изображения. Если от источника Р на линзу падает широкий пучок лучей, то лучи, составляющие разные углы j с оптической осью, пересекут ее после преломления в разных точках /рис.3/. Это явление носит название продольной сферической аберрации.
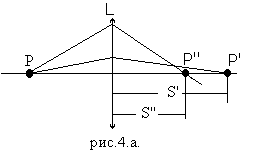 |
Для положительной линзы продольная сферическая аберрация отрицательна: S’’ – S’<0 /рис.4(а)/.
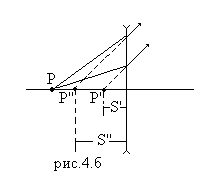 |
Для линз с отрицательной оптической силой краевые лучи преломляются меньше, чем параксиальные и величина продольной сферической аберрации положительна: S’’ – S’>0 /рис.4(б)/.
Это обстоятельство позволяет устранить сферическую аберрацию путем комбинирования положительных и отрицательных линз.
2.Хроматическая аберрация.
При освещении системы монохроматическим светом фокусное расстояние для двояковыпуклой линзы определяется соотношением:
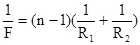
где n - показатель преломления линзы
R1 и R2 – радиусы кривизны поверхностей линз.
Для данной линзы, т.е. при определенных R1, R2 , n, величина F постоянна. При сложном составе света необходимо учитывать зависимость коэффициента преломления n от длины волны. С увеличением длины волны n уменьшается. Поэтому обыкновенная линза имеет большую оптическую силу для фиолетовых лучей, чем для красных. В результате изображение полученное от источника, испускающего белый свет, размыто и по краям окрашено. Это явление носит название хроматической аберрации.
Пусть от точечного источника света Р /рис.5/ получается изображение с помощью одной положительной линзы.
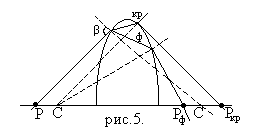 |
В этом случае изображение источника в фиолетовых лучах Р’ф расположится ближе всего к линзе, а в красных лучах Р’кр – дальше всего от линзы. Между ними расположится изображения, образованные лучами разных цветов. Устранение хроматической аберрации осуществляется комбинированием линз c различными показателями преломления, благодаря чему различные цветные изображения совмещаются, давая в фокальной плоскости изображение, не имеющее радужной окраски. Проделываем расчет для простейшего случая системы двух линз с оптическими силами
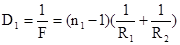 (1)
(1)

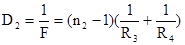 (2)
(2)
Если линзы сложены вплотную, то оптическая сила системы равна:
D=D1 + D2 (3)
Хроматическая аберрация, будет отсутствовать в том случае, если оптическая сила системы D не зависит от длины волны, т.е. D=const
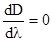
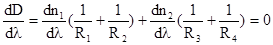
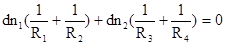 (4)
(4)
Принципиально невозможно рассчитывать систему, ахроматическую для всех длин волн. Возможно совмещение лишь двух разноцветных изображений соответствующих двум выбранным длинам волн. Для визуальных приборов (действующих совместно с глазом наблюдателя) в качестве таких волн выбираются lс=656,3 нм и lf=486,1 нм.
Цвета соответствующие этим волнам – красный и зелено-голубой являются дополнительными и при наложении дают ощущение белого света.
Для стекла первой линзы: dn1=(nf – nc)1
Для стекла второй линзы: dn2=(nf – nc)2
Записав формулы (1) и (2) для n1 и n2 соответствующих произвольной длине волны, например, lD=589,3 нм и подставляя значения dn1 и dn2 в (4), получим три уравнения:
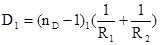 (5)
(5)
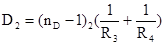 (6)
(6)
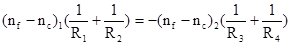 (7)
(7)
Разделим обе части последнего уравнения на D1D2 и после преобразования получим:
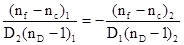
или
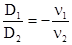 (8)
(8)
где 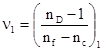 и
и 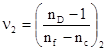 - коэффициенты дисперсии стекол линз.
- коэффициенты дисперсии стекол линз.
Формула (8) выражает условие ахроматизации двухлинзового объектива. Так как коэффициенты дисперсии имеют одинаковые знаки, то знак минус в формуле (8) показывает, что D1 и D2 имеют разные знаки, т.е. ахроматизация может быть достигнута путем соединения собирающей линзы с рассеивающей. Из уравнения (3) и (8) легко можно получить:

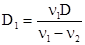 (9)
(9)
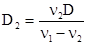 (10)
(10)
Обычно линзы в объективах склеены между собой. Поэтому радиусы кривизны соприкасающихся поверхностей делают одинаковыми R2=R3. Целесообразно, кроме того, последнюю поверхность делать плоской R4=∞. тогда из формулы (6)
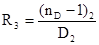 (11)
(11)
Поставим в формулу (5) вместо 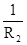 равное ему значение
равное ему значение 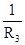 найденное из (11) получим:
найденное из (11) получим:
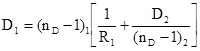
Откуда:
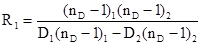 (12)
(12)
Таким образом для того, чтобы рассчитать объектив с заданной оптической силой D, состоящей из двух линз, стекла которых имеют дисперсии ν1 ν2, поступают следующим образом:
1. определяют значения D1 и D2 по формулам (9) и (10).
2. вычисляют R1 по формуле (12) и R2=R3 по формуле (11).
3.Астигматизм. Изучение астигматизма косых пучков света при их преломлении в линзе.
Если достаточно тонкий, пучок лучей, выходящих из одной точки, падает на линзу под значительным углом к оси линзы, то он в результате прохождения линзы перестанет быть гомоцентрическим. Эта потеря гомоцентричности называют астигматизмом. Изображение точки в этом случае получается стигматическим, т.е. не точечным, а в виде двух пространственно разделенных фокальных линий. Чтобы объяснить это, рассмотрим волновую поверхность элементарного пучка, т.е. поверхность нормальную к лучам. Волновая поверхность гомоцентрического пучка в однородной и изотропной среде является сферической поверхностью. Если в результате преломления пучок перестанет быть гомоцентрическим, то волновая поверхность такого пучка уже не будет сферической.
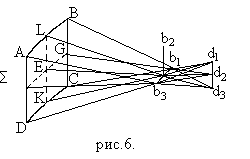 |
Пусть элемент поверхности Σ /рис.6./ является волновой поверхностью элементарного не гомоцентрического пучка.
На каждой поверхности существует два семейства кривых, пересекающихся под прямым углом, так называемые линии кривизны. Линии кривизны определяются как линии, нормальные сечения вдоль которых имеют наибольшую или наименьшую для данной точки поверхности кривизну. Для бесконечно малого элемента поверхности нормали, восстановленные вдоль линии кривизны, пересекаются в соответствующем центре кривизны поверхности. Величина отрезка нормали между поверхностью и центром кривизны равна одному из двух радиусов кривизны.
Пусть элемент поверхности Σ ограничен линиями кривизны. Тогда нормали, восстановленные вдоль линии кривизны АB (например, лучи d3В и А’d3) пересекаются в точке d3. Нормали восстановленные вдоль другой линии кривизны AD (например лучи Аb3 и Db3) пересекаются в другой точке b3 Точки d3 и b3 являются двумя центрами кривизны, а отрезки Ad3 и Bd3 двумя главными радиусами кривизны поверхности Σ. Совокупность всех центров кривизны для элемента волновой поверхности Σ образует две фокальные линии b2b3 и d1d2.
Если для бесконечно малого элемента поверхности оба главных радиуса кривизны равны, то этот бесконечно малый элемент является сферическим. В этом случае две фокальные линии сливаются в один фокус (гомоцентрический пучок).
Если через некоторый средний луч из падающего элементарного пучка и ось линзы можно провести плоскость, то эта плоскость называется меридиональной плоскостью. Лучи, идущие в меридиональной плоскости не выходят из нее в результате преломления в линзе. после прохождения линзы эти лучи соберутся в одну точку меридиональной линии. Вследствие симметрии меридиональная фокальная линия перпендикулярна меридиональной плоскости. Вторая фокальная линия лежит в меридиональной плоскости и называется сагиттальной. Она образуется лучами, идущими в сагиттальных плоскостях, т.е. в плоскостях, перпендикулярных меридиональной. Можно сказать, что современное искусство оптотехники практически преодолело все эти трудности, и в настоящее время при помощи особых приемов в шлифовке стекол и подбором стекол имеем оптические системы, свободные от перечисленных недостатков. но для возможности этой практики и для ее обоснования потребовалось сделать много теоретических выкладок. В этой области следует отметить таких ученых как Эйлер, Даламбер, Гаусс, Аббе, Релей. Они делали совершенную теорию оптических инструментов.
Эту теорию по новому пути продвинул Д.Д.Максутов. воспроизведение неискаженных, оптических изображений сводится к возможному устранению перечисленных выше недостатков, а это приводит к необходимости подбора и сочетания различных сортов стекла, что доведено современными оптиками до высокой степени совершенства.
В настоящее время многие учреждения выработали приемы варки высоких сортов стекла. У нас во главе этой промышленности стоит Государственный оптический институт (С. Петербург), созданный усилиями академика Д.С.Рождественского.
Оптическое стекло имеет очень сложный состав, который постепенно определяется сообразно требованиям приборостроения. В виде примера приведем состав некоторых сортов стекла:
1. Легкий флинт (n=1,5480); SiO2 – 61%; Na2O – 4.5;K2O – 8; PbO – 26.3; As2O3 – 0.2.
2. Тяжелый флинт (n=1,7550); SiO2 – 31.6%; K2O – 2.8;PbO – 65.3; As2O3 – 0.2.
3. Баритовый крон (n=1,5302); SiO2 – 63.1%; B2O2 – 3.2; K2O – 10.4; BaO – 14.7; ZnO – 5.2; As2O3 – 0.2.
4. Тяжелый крон (n=1,5726); SiO2 – 50.2%; B2O3 – 3.3; K2O – 6.1; BaO – 30.2; ZnO – 9.5; Sb2O3 – 0.5; As2O3 – 0.1.
4.Дисторсия.
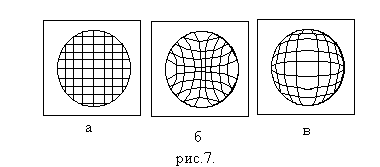 |
Дисторсия представляет собой дефект, свойственный не точечному источнику света, а предметам, имеющим конечные размеры. Дисторсией называют искажение изображения, обусловленное неодинаковостью поперечного увеличения в пределах поля зрения. Благодаря этому нарушается подобие между предметом и его изображением. Наиболее отчетливо проявляется дисторсия, когда предметом является плоская сетка. На рис.7. показаны различные виды дисторсии: сетка (рис.7(а)) принимает вид рис. 7(б) – подушкообразная или рис.7(в) – бочкообразная дисторсия.
Бочкообразная дисторсия возникает тогда, когда поперечное увеличение уменьшается по мере удаления от оптической оси. Подушкообразная дисторсия возникает тогда, когда поперечное увеличение возрастает по мере удаления от оси.
В приборах, предназначенных для визуального наблюдения, дисторсия обычно не имеет большого значения, однако в тех случаях, когда изображение используется для измерений, особенно для точных измерений (аэрофотосъемки, инструментальные микроскопы), тогда дисторсия недопустима. для этих целей необходимо применять системы линз, исправленные в отношении дисторсии.
Методика измерений.
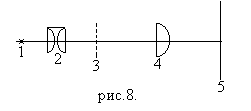 |
Экспериментальная установка собрана на основе оптической скамьи ФОС и изображена на рис.8.
где 1-лампа накаливания
2-конденсор оптической скамьи
3-предмет – миллиметровая сетка на стеклянной пластинке
4-плоско-выпуклая линза
5-экран
Линза расположена плоской поверхностью к источнику.
Библиографический список.
1. Сивухин Д.В. Оптика.-М,: Наука, 1985
2. Фриш С.Э. и Тиморева А.В. Курс общей физики. Т.3.
3. Королев Ф.А. Курс физики. Оптика, атомная и ядерная физика. – М.: просвещение. 1974
4. Корсунский. Оптика, строение атома, атомное ядро.-М.: Наука 1967
5. Иверонова. Физический практикум.
| <== предыдущая лекция | | | следующая лекция ==> |
| Определение вагоно-часов простоя под грузовыми операциями | | | Электроэнергетика – специфическая отрасль |
Дата добавления: 2017-11-21; просмотров: 925;











