Метод интегрирования по частям.

Пусть u = u(x) и v = v(x) – непрерывно дифференцируемые функции. По правилу дифференцирования произведения имеем

d(uv) = vdu + udv , откуда udv = d(uv) – vdu .

Интегрируя это равенство, получим (используя свойство 2)

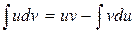
Эту формулу называют формулой интегрирования по частям. Она обычно применяется при интегрировании выражений, которые можно представить в виде произведения двух сомножителей и и dv так, чтобы отыскание функции v по ее дифференциалу dv и вычисление интеграла 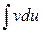составляли в совокупности задачу более простую, чем вычисление исходного интеграла .

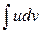Пример 5.

.

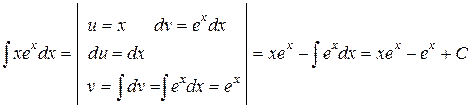Заметим, что нахождение функции v сводится к вычислению интеграла 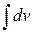, причем для наших целей достаточно хотя бы одним способом представить выражение cosxdx в виде dv, и значит, нет надобности писать для v выражение, содержащее константу. Это замечание следует иметь в виду и впредь.

Успешность применения метода интегрирования по частям зависит от того, насколько удачно будет произведено представление подынтегрального выражения в виде произведения u.dv. Рассмотрим некоторые рекомендации по такому выбору.

Пусть требуется, используя метод интегрирования по частям, найти интеграл 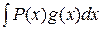, где Р(х) – многочлен (или рациональная функция), а g(x) – произвольная непрерывная функция. Тогда выбор функции и и выражения dv осуществляют так:

1. если 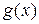– любая из функций 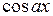, , 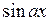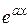(а – константа), то выбор следующий: и = Р(х), ;

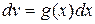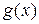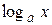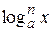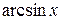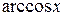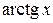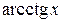2. если – любая из функций , , , , или , то выбор следующий: и = g(х), ;

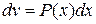Так же как и замену переменных, интегрирование по частям можно применять несколько раз. Можно также комбинировать все рассмотренные методы.

Любопытный пример представляют интегралы 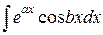и 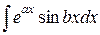. Их называют циклическими, поскольку применение в этих интегралах дважды метода интегрирование по частям приводит обратно к исходным интегралам. Предлагаем вам самостоятельно вычислить эти интегралы.