Матрица перехода от одного базиса ЛП к другому.
Пусть дана система векторов {а1, а2, …, аk } линейного пространства L и известны координаты этих векторов в некотором базисе Б:
а1= (а11, а21, …, ап1),
а 2= (а12, а22, …, ап2),
. . . . . . . . . . . . . . . . . .
аk= (а1k, а2k, …, апk).
Рассмотрим матрицу этой системы векторов, т.е. матрицу, столбцы которой есть координаты векторов системы в заданном базисе:
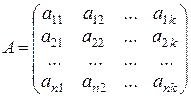 .
.
Оказывается, с помощью ранга матрицы системы векторов можно сделать вывод о линейной зависимости или независимости этих векторов. А именно, справедлива следующая теорема.
Теорема 3
Для того чтобы k векторов п-мерного линейного пространства были линейно независимы, необходимо и достаточно, чтобы ранг матрицы этой системы был равен k.
Как уже отмечалось, координаты вектора зависят от выбранного базиса. Рассмотрим два базиса Б1:{а1, а2, …, ап} и Б2:{ 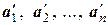 } линейного пространства L. Так как векторы
} линейного пространства L. Так как векторы 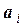 и
и 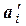 есть векторы одного и того же линейного пространства L, то векторы базиса Б2 можно разложить по базису Б1. Пусть эти разложения имеют вид
есть векторы одного и того же линейного пространства L, то векторы базиса Б2 можно разложить по базису Б1. Пусть эти разложения имеют вид
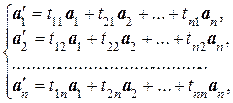 откуда
откуда 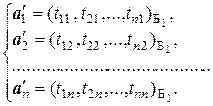
Определение 3
Матрица векторов базиса Б2 в базисе Б1 называется матрицей перехода от базиса Б1 к базису Б2 и обозначается 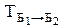 или просто Т.
или просто Т.
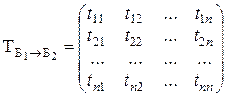 . (2.2)
. (2.2)
Матрица 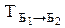 перехода от одного базиса к другому есть невырожденная квадратная матрица.
перехода от одного базиса к другому есть невырожденная квадратная матрица.
Рассмотрим произвольный вектор хлинейного пространств L. Пусть известны координаты этого вектора в базисе Б1 и в базисе Б2:
х 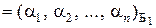 , х
, х 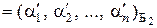 .
.
Обозначим соответствующие координатные столбцы 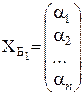 и
и 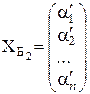 . Тогда имеют место формулы преобразования координат:
. Тогда имеют место формулы преобразования координат:
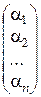 =
= 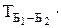
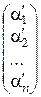 и
и 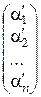 =
= 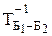 ×
× 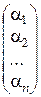 ,
,
или в матричной форме
Х 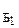 =
= 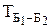 ×Х
×Х 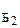 , Х
, Х 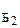 =
= 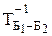 ×Х
×Х 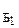 .
.
Дата добавления: 2017-11-21; просмотров: 3100;











